Zentralprojektion
Mit Hilfe der Zentralprojektion stellt man in der darstellenden
Geometrie anschauliche Bilder von räumlichen Objekten her. Im Gegensatz zur
Parallelprojektion,
wo man parallele Strahlen zur Projektion auf eine Ebene (Bildtafel) verwendet,
benutzt man bei der Zentralprojektion Strahlen (Geraden) durch einen festen
Punkt ,
den Augpunkt. Die Zentralprojektion erzeugt Bilder, wie sie auch beim Sehen mit
einem Auge im Augpunkt entstehen. Während bei der Parallelprojektion parallele
Geraden auf ebensolche abgebildet werden, werden bei der Zentralprojektion
parallele Geraden, die nicht parallel zur Bildtafel verlaufen, auf Geraden
abgebildet, die sich in einem Punkt, dem Fluchtpunkt,
schneiden. Zentralprojektionen geben den räumlichen Eindruck eines Objektes viel
besser wieder als eine Parallelprojektion (s. Häuserreihe). Die
Zentralprojektion entspricht der Abbildung der Umwelt durch das menschliche Auge und ergibt somit
einen natürlichen Bildeindruck. Sie wird in Technik
und Architektur, in der Kartografie, in der Malerei und
beim Zeichnen,
sowie in der Computergrafik
angewendet.
Bezeichnungen
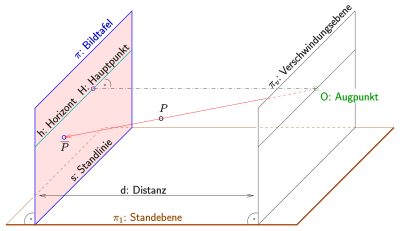

Den Augpunkt, das Zentrum der Projektionsstrahlen einer
Zentralprojektion, bezeichnet man üblicherweise mit O, womit eine Beziehung zum
Auge (lat.: oculus = Auge) hergestellt wird. Den Lotfußpunkt vom Augpunkt auf
die Bildtafel nennt man Hauptpunkt, da er bei der Herstellung einer
Zentralprojektion und beim anschließenden Betrachten eine wichtige Rolle spielt.
Der Hauptpunkt ist sozusagen der Mittelpunkt des Bildes. Der Abstand des
Augpunktes von der Bildtafel heißt Distanz (der aktuellen
Zentralprojektion). Ist der Hauptpunkt im Bild gekennzeichnet und die Distanz
bekannt, so weiß man, wo man beim Betrachten des Bildes das Auge positionieren
muss, um einen perfekten Eindruck zu erhalten. Der Fluchtpunkt eines
parallelen Geradenbüschels, das nicht zur Bildtafel parallel ist, ist der
gemeinsame Schnittpunkt der zugehörigen Bildgeraden und ist immer der
Schnittpunkt mit der Bildtafel (Spurpunkt) derjenigen Gerade des Büschels, die
den Augpunkt enthält (s. Bild). Geraden, die zur Bildtafel parallel sind, haben
also keine Fluchtpunkte oder man sagt, der zugehörige Fluchtpunkt liegt im
„Unendlichen“. Eine Gerade, die senkrecht zur Bildtafel verläuft nennt man
Tiefenlinie. Der Fluchtpunkt aller Tiefenlinien ist der Hauptpunkt. Bei
vielen Objekten spielen horizontale Geraden und damit deren Fluchtpunkte eine
wichtige Rolle. Die Fluchtpunkte aller horizontalen Richtungen bilden zusammen
den Horizont h, eine horizontale Gerade. Falls die Bildtafel senkrecht
steht, liegt der Hauptpunkt immer auf dem Horizont. Quaderförmige Objekte haben
a) drei natürliche Fluchtpunkte, wenn keine der Kanten parallel zur Bildtafel
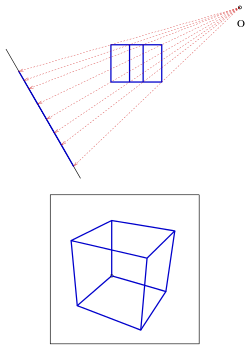
ist (s. Bild des Würfels im ersten Bild), b) zwei Fluchtpunkte, wenn eine Kante
parallel zur Bildtafel ist (s. 1. Haus), c) einen Fluchtpunkt, wenn zwei
Richtungen parallel zur Bildtafel verlaufen (s. 2. Haus). Den letzten Fall nennt
man Frontalperspektive. Meistens werden Zentralprojektionen von Objekten
mit Hilfe von Auf- und Grundrissen hergestellt. Die Grundrissebene wird in
Anlehnung an das Fotografieren als die Standebene (des Betrachters)
bezeichnet. Die Schnittgerade (Spurgerade) s der Grundrissebene (Standebene) mit
der Bildtafel wird oft aus technischen Gründen mit in das Bild eingezeichnet und
Standlinie genannt. Standlinie und Horizont sind immer parallel
zueinander. Mit Hilfe von Strahlen durch den Augpunkt O lassen sich alle Punkte
des Raumes außer den Punkten in der zur Bildtafel parallelen Ebene
durch den Augpunkt abbilden. Die Punkte dieser Ebene nennt man
Verschwindungspunkte und die Ebene
Verschwindungsebene. Beim Betrachten einer Zentralprojektion hat man oft
den Eindruck, dass Randbereiche verzerrt erscheinen. Dies liegt immer daran,
dass man sein Auge nicht im Augpunkt positioniert hat. Den Bereich des Bildes,
den man nämlich bei Positionierung des Auges im Augpunkt und Fixierung des
Hauptpunktes noch überblicken kann, ist erfahrungsgemäß kegelförmig
eingeschränkt. Den Schnitt dieses Sehkegels mit der Bildtafel ist der Sehkreis (s.
Bild einer Brücke). Sein Radius beträgt ungefähr 0.58*Distanz. Dies entspricht
einem halben Öffnungswinkel des Sehkegels von 30°.
In der darstellenden Geometrie bildet man immer Objekte ab „vor“ der
Verschwindungsebene
ab, d.h. Objekt und Bildtafel befinden sich auf derselben Seite der
Verschwindungsebene. Bei der Fotografie liegen Objekt und Bild immer auf
verschiedenen Seiten von
.
Dadurch stehen fotografische Bilder in der Kamera immer „auf dem Kopf“, was auf
das Betrachten später keinen Einfluss hat, da man das Bild dann einfach „richtig
herum“ hält.
Der Vorteil einer Zentralprojektion ist, dass sie sehr anschauliche Bilder liefert, nämlich Bilder, die das Sehen (mit einem Auge) oder das Fotografieren nachahmen. Allerdings lassen sich Längen aus einer Zentralprojektion oder auch nur Verhältnisse von Längen nicht ablesen. Denn im Gegensatz zur Parallelprojektion, die verhältnistreu ist, bleibt bei einer Zentralprojektion nur das Doppelverhältnis (Verhältnis von Verhältnissen) invariant.
Die Zentralprojektion stellt Objekte im Randbereich zu groß dar. So werden die Felder eines Schachbretts, welches zur Bildtafel parallel liegt, alle gleich groß und quadratisch abgebildet. Tatsächlich sind die weiter vom Hauptpunkt entfernt liegenden Felder auch weiter vom Betrachter entfernt und müssten auf der Bildtafel kleiner dargestellt werden, um eine natürliche Abbildung zu erhalten. In der Tat wird dieser Effekt bei Abbildungen mit Fischaugenobjektiven sichtbar. Der menschliche Sehapparat korrigiert jedoch die entstehenden verkrümmten Kanten bei der Betrachtung großer, naher Objekte, so dass die Fischaugenperspektive gerade nicht natürlich erscheint.
Viele Weitwinkelobjektive nähern sich daher der Zentralperspektive an, indem sie randnahe Bildpartien vergrößert darstellen, so dass die parallel zur Bildtafel liegenden Geraden auch möglichst gerade abgebildet werden. Dies führt zwar zu gewissen Verzerrungen in den Bildecken, die aber in der Architekturfotografie nicht als störend empfunden werden und bei Landschaftsaufnahmen eine gewisse, gegebenenfalls erwünschte Dramatik hervorrufen, während die Abbildung von Personengruppen mit einem Weitwinkelobjektiv häufig zu unbefriedigenden Ergebnissen führt. Video-Aufnahmen mit Weitwinkel führen bei Schwenks zu unnatürlichem "Fließen" der in die Randbereiche geratenden Objekte. Die beschriebenen Zusammenhänge fallen bei Brennweiten mit Sehkegeln weiter als dem menschlichen auf.
Zur Bedeutung von Hauptpunkt, Distanz und Augpunkt
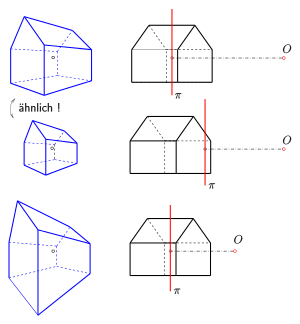
Das Bild mit Variationen eines Hauses zeigt die Bedeutung der wesentlichen
Parameter Hauptpunkt, Distanz und Augpunkt. Hält man den Augpunkt
fest und schiebt die Bildtafel auf den Augpunkt zu, d.h. man verkürzt die
Distanz, so wird das Bild lediglich verkleinert auf ein zum ersten Bild ähnliches
Bild. Winkel bleiben dabei erhalten. Hält man dagegen die Bildtafel fest und
schiebt den Augpunkt
auf den Hauptpunkt zu, d.h. auch hier wird die Distanz verkürzt, so
entsteht ein Bild mit einer neuen Bildwirkung. Das Bild ist nicht mehr ähnlich
zum ersten Bild. Entsprechende Winkel sind nicht mehr gleich. Eine Verschiebung
des Hauptpunktes entlang der Gerade
bewirkt lediglich eine Verkleinerung oder Vergrößerung des Bildes. Eine
Verschiebung des Augpunktes entlang
bewirkt eine wesentliche Veränderung des Bildes.
Konstruktion der Zentralprojektion eines Objektes
Die Konstruktion einer Zentralprojektion eines Objektes ist deutlich aufwendiger als eine Parallelprojektion. Hierzu gibt es ein dem Einschneideverfahren für Parallelprojektionen ähnliches Verfahren: die Architektenanordnung. Wie beim Einschneideverfahren müssen Grund- und Aufriss besonders positioniert werden. Für die Konstruktion des Bildes werden nur Punkte verbunden und Geraden geschnitten. Parallelen spielen bei der Parallelprojektion eine wichtige erleichternde Rolle. Auch bei Zentralprojektion sind sie durch ihre Fluchtpunkte eine große Hilfe. Eine weitere relativ einfache Methode ist die Frontalperspektive. Sie ähnelt der Kavaliersperspektive für eine Parallelprojektion (Axonometrie). Bei der Frontalperspektive ist die Bildtafel zu einer wesentlichen Ebene des Objekts, z.B. einer Hausfront, parallel oder die Bildtafel und diese wesentliche Ebene sind identisch. Letzteres hat den großen Vorteil, dass man einfach den Aufriss des Objektes zur Frontalperspektive ausbauen kann. Ein weiterer wichtiger Vorteil einer Frontalperspektive ist, dass Kreise in der wesentlichen Ebene wieder auf Kreise abgebildet werden (Frontalperspektive). Allerdings gibt es auch einen Nachteil: Die Frontebene des Objektes wird stark betont. Bei einer Zentralprojektion mit zwei wesentlichen Fluchtpunkten ist dies meistens nicht der Fall.
Projektionsformeln
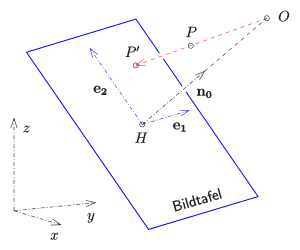
Zur analytischen Beschreibung der Zentralprojektion wählen wir in der Bildtafel
- den Hauptpunkt
als Koordinatenursprung eines neuen Koordinatensystems und
- den Normaleneinheitsvektor der Bildtafel
, der von
zum Augpunkt
zeigt.
- Mit der Distanz
gilt:
.
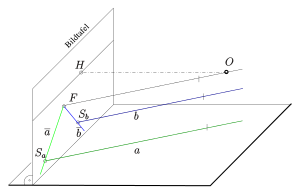
- Wir ergänzen
durch Einheitsvektoren
so, dass
- a)
horizontal ist und b)
ein Orthonormalsystem bilden (s. Bild).
Die Zentralprojektion eines Objektpunktes
wird in zwei Schritten durchgeführt:
- Koordinatentransformation des Punktes
in das System
mit dem Nullpunkt
und der Basis
:
mit
- Zentralprojektion in dem System
auf die
- Ebene:
Eine anschauliche Beschreibung des Normalenvektors
erhält man, wenn man die Winkelkoordinaten
der Kugelkoordinaten
verwendet. Der Winkel
beschreibt (im Bogenmaß) die geographische Länge und
die geographische Breite:
Für die Vektoren
erhält man dann:
.
Um eine konkrete Zentralprojektion festzulegen, müssen
- a) der Hauptpunkt
, b) die Distanz
und c) die zwei Winkel
angegeben werden.
Insgesamt sind also 6 Zahlen nötig.
Bemerkung: Für
erhält man die Formeln für die senkrechte Parallelprojektion. Da der Hauptpunkt
hier keine Rolle mehr spielt, kann man
setzen. Man erkennt, dass eine senkrechte Parallelprojektion durch eine lineare Abbildung
beschrieben wird. Dies gilt nicht für eine Zentralprojektion.
Bemerkung: Bei der Auswertung von Messbildern in der Photogrammetrie kommen andere Parameter zum Einsatz, s. Orientierung.
Anwendungen der Zentralprojektion
Typische Anwendungen der Zentralprojektion finden sich:
- in der Computergrafik
- in der Fotografie z.B. bei der Rekonstruktion von Gebäuden aus Fotografien
- in der Photogrammetrie z.B bei der Auswertung und Ausmessung von (Luft-)Bildern, beim Entzerren von Schrägaufnahmen,


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 24.04. 2022