Abbildungsmatrix

Eine Abbildungs- oder Darstellungsmatrix ist eine Matrix (also eine rechteckige Anordnung von Zahlen), die in der linearen Algebra verwendet wird, um eine lineare Abbildung zwischen zwei endlichdimensionalen Vektorräumen zu beschreiben.

Die aus diesen abgeleiteten affinen Abbildungen, Affinitäten und Projektivitäten können ebenfalls durch Abbildungsmatrizen dargestellt werden.

Begriff

Voraussetzungen

Um eine lineare Abbildung von Vektorräumen durch eine Matrix beschreiben zu können, muss zunächst sowohl im Urbildraum als auch im Zielraum eine Basis (mit Reihenfolge der Basisvektoren) fest gewählt worden sein. Bei einem Wechsel der Basen in einem der betroffenen Räume muss die Matrix transformiert werden, sonst beschreibt sie eine andere lineare Abbildung.

Wenn in der Definitionsmenge und der Zielmenge eine Basis gewählt worden ist, dann lässt sich eine lineare Abbildung eindeutig durch eine Abbildungsmatrix beschreiben. Allerdings muss dafür festgelegt werden, ob man die Koordinaten von Vektoren in Spalten- oder Zeilenschreibweise notiert. Die üblichere Schreibweise ist die in Spalten.

Dazu muss man den Vektor, der abgebildet werden soll, als Spaltenvektor (bzgl. der gewählten Basis) schreiben.

Aufbau bei Verwendung von Spaltenvektoren

Nach der Wahl einer Basis aus der Definitionsmenge und der Zielmenge stehen in den Spalten der Abbildungsmatrix die Koordinaten der Bilder der Basisvektoren des abgebildeten Vektorraums bezüglich der Basis des Zielraums: Jede Spalte der Matrix ist das Bild eines Vektors der Urbildbasis. Eine Abbildungsmatrix, die eine Abbildung aus einem 4-dimensionalen Vektorraum in einen 6-dimensionalen Vektorraum beschreibt, muss daher stets 6 Zeilen (für die sechs Bildkoordinaten der Basisvektoren) und 4 Spalten (für jeden Basisvektor des Urbildraums eine) haben.

Allgemeiner: Eine lineare Abbildungsmatrix $M_{B}^{A}(f)$ aus einem n-dimensionalen Vektorraum mit Basis in einen m-dimensionalen Vektorraum mit Basis hat m Zeilen und n Spalten. Das Bild eines Koordinatenvektors unter der linearen Abbildung kann man dann so berechnen:

$M_{B}^{A}(f)\cdot {\vec {x}}={\vec {y}}$

Dabei ist ${\vec {y}}$ der Bildvektor, ${\vec {x}}$ der Vektor, der abgebildet wird, jeweils in den zur gewählten Basis ihres Raumes gehörenden Koordinaten.

Siehe hierzu auch: Aufbau der Abbildungsmatrix.

Verwendung von Zeilenvektoren

Verwendet man anstelle von Spaltenvektoren Zeilenvektoren, dann muss die Abbildungsmatrix transponiert werden. Das bedeutet, dass nun die Koordinaten des Bildes des 1. Basisvektors im Urbildraum in der ersten Zeile stehen usw. Bei der Berechnung der Bildkoordinaten muss der (Zeilenkoordinaten-)Vektor nun von links an die Abbildungsmatrix multipliziert werden.

Berechnung

Abbildungen auf Koordinatentupel

Sei $f\colon V\to \mathbb {R} ^{m}$ eine lineare Abbildung und

$A=({\vec {v}}_{1},{\vec {v}}_{2},\dotsc ,{\vec {v}}_{n})$

eine geordnete Basis von .

Als Basis für die Zielmenge $\mathbb {R} ^{m}$ wird die Standardbasis gewählt:

$B=({\vec {e}}_{1},{\vec {e}}_{2},\dotsc ,{\vec {e}}_{m})$

Die Abbildungsmatrix ergibt sich, indem man die Bilder der Basisvektoren von als Spalten einer Matrix auffasst

$M_{B}^{A}(f)={\begin{pmatrix}\vert &\vert &&\vert \\f({\vec {v}}_{1})&f({\vec {v}}_{2})&\cdots &f({\vec {v}}_{n})\\\vert &\vert &&\vert \end{pmatrix}}.$

Beispiel: Man betrachte die lineare Abbildung

$f\colon \mathbb {R} ^{3}\to \mathbb {R} ^{2},f{\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}2x-3y\\x-2y+z\end{pmatrix}}.$

Sowohl im Urbildraum $\mathbb {R} ^{3}$ als auch im Zielraum $\mathbb {R} ^{2}$ wird die Standardbasis gewählt:

$A=\left({\begin{pmatrix}1\\0\\0\end{pmatrix}},{\begin{pmatrix}0\\1\\0\end{pmatrix}},{\begin{pmatrix}0\\0\\1\end{pmatrix}}\right)\,,\quad B=\left({\begin{pmatrix}1\\0\end{pmatrix}},{\begin{pmatrix}0\\1\end{pmatrix}}\right)$

Es gilt:

$f{\begin{pmatrix}1\\0\\0\end{pmatrix}}={\begin{pmatrix}2\\1\end{pmatrix}},\quad f{\begin{pmatrix}0\\1\\0\end{pmatrix}}={\begin{pmatrix}-3\\-2\end{pmatrix}},\quad f{\begin{pmatrix}0\\0\\1\end{pmatrix}}={\begin{pmatrix}0\\1\end{pmatrix}}$

Damit ist die Abbildungsmatrix von bezüglich der gewählten Basen und

$M_{B}^{A}(f)={\begin{pmatrix}2&-3&0\\1&-2&1\end{pmatrix}}.$

Abbildungen in allgemeine Vektorräume

Falls die Elemente des Zielraums keine Koordinatentupel sind, oder aus anderen Gründen eine andere Basis $B=({\vec {w}}_{1},{\vec {w}}_{2},\dotsc ,{\vec {w}}_{m})$ anstelle der Standardbasis gewählt wird, so müssen die Bilder $f({\vec {v}}_{j})$ als Linearkombinationen der Basisvektoren ${\vec {w}}_{i}$ dargestellt werden, um die Einträge $a_{ij}$ der Abbildungsmatrix zu ermitteln:

$f({\vec {v}}_{j})=a_{1j}{\vec {w}}_{1}+a_{2j}{\vec {w}}_{2}+\dotsb +a_{mj}{\vec {w}}_{m}=\sum _{i=1}^{m}a_{ij}{\vec {w}}_{i}$

Die Abbildungsmatrix ergibt sich dann, indem man die Koeffizienten der Linearkombinationen spaltenweise in die Matrix einträgt:

$M_{B}^{A}(f)={\begin{pmatrix}a_{11}&\dots &a_{1j}&\dots &a_{1n}\\a_{21}&\dots &a_{2j}&\dots &a_{2n}\\\vdots &&\vdots &&\vdots \\a_{m1}&\dots &a_{mj}&\dots &a_{mn}\end{pmatrix}}$

Beispiel: Es werde wieder die lineare Abbildung des obigen Beispiels betrachtet. Diesmal wird im Zielraum $\mathbb {R} ^{2}$ jedoch die geordnete Basis

$B=\left({\begin{pmatrix}2\\1\end{pmatrix}},{\begin{pmatrix}1\\1\end{pmatrix}}\right)$

verwendet. Nun gilt:

$f{\begin{pmatrix}1\\0\\0\end{pmatrix}}={\begin{pmatrix}2\\1\end{pmatrix}}=1\,{\begin{pmatrix}2\\1\end{pmatrix}}+0\,{\begin{pmatrix}1\\1\end{pmatrix}},$

$f{\begin{pmatrix}0\\1\\0\end{pmatrix}}={\begin{pmatrix}-3\\-2\end{pmatrix}}=-1\,{\begin{pmatrix}2\\1\end{pmatrix}}-1\,{\begin{pmatrix}1\\1\end{pmatrix}},$

$f{\begin{pmatrix}0\\0\\1\end{pmatrix}}={\begin{pmatrix}0\\1\end{pmatrix}}=-1\,{\begin{pmatrix}2\\1\end{pmatrix}}+2\,{\begin{pmatrix}1\\1\end{pmatrix}}$

Damit erhält man für Abbildungsmatrix von bezüglich der Basen und :

$M_{B}^{A}(f)={\begin{pmatrix}1&-1&-1\\0&-1&2\end{pmatrix}}$

Koordinatendarstellung von linearen Abbildungen

Mit Hilfe der Abbildungsmatrix kann man den Bildvektor $f({\vec {v}})$ eines Vektors ${\vec {v}}\in V$ unter der linearen Abbildung $f\colon V\to W$ berechnen.

Hat der Vektor ${\vec {v}}\in V$ bezüglich der Basis $A=({\vec {v}}_{1},\dotsc ,{\vec {v}}_{n})$ den Koordinatenvektor

${\vec {v}}_{A}={\vec {x}}={\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}}$ ,

das heißt

${\vec {v}}=x_{1}{\vec {v}}_{1}+\dotsb +x_{n}{\vec {v}}_{n}$ ,

und hat der Bildvektor $f({\vec {v}})$ bezüglich der Basis $B=({\vec {w}}_{1},\dotsc ,{\vec {w}}_{m})$ von die Koordinaten

$f({\vec {v}})_{B}={\vec {y}}={\begin{pmatrix}y_{1}\\\vdots \\y_{m}\end{pmatrix}}$ ,

das heißt

$f({\vec {v}})=y_{1}{\vec {w}}_{1}+\dotsb +y_{m}{\vec {w}}_{m}$ ,

so gilt

$y_{i}=\sum _{j=1}^{n}a_{ij}\,x_{j}$ ,

bzw. mit Hilfe der Abbildungsmatrix $M_{B}^{A}(f)=(a_{ij})$ ausgedrückt:

${\begin{pmatrix}y_{1}\\\vdots \\y_{m}\end{pmatrix}}={\begin{pmatrix}a_{11}&\dots &a_{1n}\\\vdots &\ddots &\vdots \\a_{m1}&\dots &a_{mn}\end{pmatrix}}\cdot {\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}}$ ,

kurz

${\vec {y}}=M_{B}^{A}(f)\cdot {\vec {x}}$

bzw.

$f({\vec {v}})_{B}=M_{B}^{A}(f)\cdot {\vec {v}}_{A}$ >.

Hintereinanderausführung von linearen Abbildungen

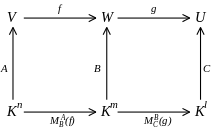
Kommutatives Diagramm zur Übersicht

Der Hintereinanderausführung von linearen Abbildungen entspricht das Matrizenprodukt der zugehörigen Abbildungsmatrizen:

Es seien , und Vektorräume über dem Körper und $f\colon V\to W$ und $g\colon W\to U$ lineare Abbildungen. In sei die geordnete Basis $A=({\vec {v}}_{1},\dots ,{\vec {v}}_{n})$ gegeben, in die Basis $B=({\vec {w}}_{1},\dots ,{\vec {w}}_{m})$ und die Basis $C=({\vec {u}}_{1},\dots ,{\vec {u}}_{l})$ in . Dann erhält man die Abbildungsmatrix der verketteten linearen Abbildung

$g\circ f\colon V\to U,$

indem man die Abbildungsmatrix von und die Abbildungsmatrix von (jeweils bezüglich der entsprechenden Basen) multipliziert:

$M_{C}^{A}(g\circ f)=M_{C}^{B}(g)\cdot M_{B}^{A}(f)$

Man beachte, dass in für beide Abbildungsmatrizen dieselbe Basis gewählt werden muss.

Begründung: Es sei $M_{B}^{A}(f)=(a_{ij})$ , $M_{C}^{B}(g)=(b_{ki})$ und $M_{C}^{A}(g\circ f)=(c_{kj})$ . Die -te Spalte von $M_{C}^{A}(g\circ f)$ enthält die Koordinaten des Bilds $(g\circ f)({\vec {v}}_{j})$ des -ten Basisvektors aus bezüglich der Basis :

$\sum _{k=1}^{l}c_{kj}{\vec {u}}_{k}=(g\circ f)({\vec {v}}_{j})$

Berechnet man die rechte Seite mit Hilfe der Abbildungsmatrizen von und , so erhält man:

${\begin{aligned}(g\circ f)({\vec {v}}_{j})&=g{\big (}f({\vec {v}}_{j}){\big )}=g\left(\sum _{i=1}^{m}a_{ij}\,{\vec {w}}_{i}\right)=\sum _{i=1}^{m}a_{ij}\,g({\vec {w}}_{i})\\&=\sum _{i=1}^{m}a_{ij}\,\left(\sum _{k=1}^{l}b_{ki}\,{\vec {u}}_{k}\right)=\sum _{k=1}^{l}\left(\sum _{i=1}^{m}b_{ki}\,a_{ij}\right)\,{\vec {u}}_{k}\end{aligned}}$

Durch Koeffizientenvergleich folgt

$c_{kj}=\sum _{i=1}^{m}b_{ki}\,a_{ij}$

für alle und , also

$(c_{kj})=(b_{ki})\cdot (a_{ij})$ ,

das heißt:

$M_{C}^{A}(g\circ f)=M_{C}^{B}(g)\cdot M_{B}^{A}(f)$

Verwendung

Basiswechsel

→ Hauptartikel: Basiswechsel

Kommutatives Diagramm der beteiligten Abbildungen

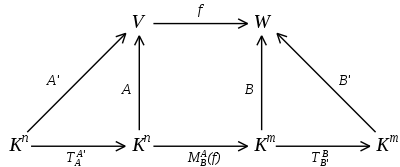
Ist die Abbildungsmatrix einer Abbildung für bestimmte Basen bekannt, so lässt sich die Abbildungsmatrix für dieselbe Abbildung, jedoch mit anderen Basen, leicht berechnen. Dieser Vorgang wird als Basiswechsel bezeichnet. Es kann etwa sein, dass die vorliegenden Basen schlecht geeignet sind, um ein bestimmtes Problem mit der Matrix zu lösen. Nach einem Basiswechsel liegt die Matrix dann in einer einfacheren Form vor, repräsentiert aber immer noch dieselbe lineare Abbildung. Die Abbildungsmatrix $M_{{B'}}^{{A'}}(f)$ berechnet sich aus der Abbildungsmatrix $M_{B}^{A}(f)$ und den Basiswechselmatrizen $T_{A}^{A'}$ und $T_{B'}^{B}$ wie folgt:

$M_{B'}^{A'}(f)=T_{B'}^{B}\cdot M_{B}^{A}(f)\cdot T_{A}^{A'}$

Beschreibung von Endomorphismen

Bei einer linearen Selbstabbildung (einem Endomorphismus) eines Vektorraums legt man gewöhnlich eine feste Basis des Vektorraumes als Definitionsmenge und Zielmenge zugrunde. Dann beschreibt die Abbildungsmatrix die Veränderung, die die Koordinaten eines beliebigen Vektors bezüglich dieser Basis bei der Abbildung erfahren. Die Abbildungsmatrix ist bei Endomorphismen stets quadratisch, d.h. die Zahl der Zeilen stimmt mit der Zahl der Spalten überein.

Beschreibung von affinen Abbildungen und Affinitäten

→ Hauptartikel: Affine Abbildung

Nach der Wahl einer affinen Punktbasis in beiden affinen Räumen, die durch eine affine Abbildung aufeinander abgebildet werden, kann diese Abbildung durch eine Abbildungsmatrix und eine zusätzliche Verschiebung oder – in homogenen Koordinaten durch eine erweiterte (auch: "homogene") Abbildungsmatrix allein beschrieben werden.

Beispiele

Orthogonalprojektion

Im dreidimensionalen Raum (mit der kanonischen Basis) kann man die Orthogonalprojektion eines Vektors auf eine Ursprungsgerade durch folgende Abbildungsmatrix beschreiben:

$A_{P_{n}}={\begin{pmatrix}n_{1}^{2}&n_{1}n_{2}&n_{1}n_{3}\\n_{1}n_{2}&n_{2}^{2}&n_{2}n_{3}\\n_{1}n_{3}&n_{2}n_{3}&n_{3}^{2}\end{pmatrix}}$

Dabei sind ${\vec {n}}=(n_{1},n_{2},n_{3})^{T}$ die Koordinaten des normierten Richtungsvektors der Geraden. Wird anstatt auf eine Gerade auf eine Ebene mit den beiden zueinander senkrechten, normierten Richtungsvektoren ${\vec {p}}$ und ${\vec {q}}$ projiziert, so kann man dies in zwei Projektionen entlang der beiden Richtungsvektoren auffassen, und demnach die Projektionsmatrix für die Orthogonalprojektion auf eine Ursprungsebene folgendermaßen aufstellen:

$A_{P_{E}}=A_{P_{p}}+A_{P_{q}}$

Die Projektionsmatrix um auf eine Ebene zu projizieren, ist also die Summe der Projektionsmatrizen auf ihre Richtungsvektoren.

Spiegelung

Wird anstatt einer Projektion eine Spiegelung durchgeführt, so kann dies ebenfalls mit Hilfe der obigen Projektionsmatrix dargestellt werden. Für die Spiegelungsmatrix an einer Ursprungsgeraden mit normiertem Richtungsvektor ${\vec {n}}$ gilt:

$A_{S_{n}}=2A_{P_{n}}-E$ ,

wobei die Einheitsmatrix darstellt. Gleiches gilt für die Spiegelung an der Ebene:

$A_{S_{E}}=2A_{P_{E}}-E$ .

Für die Spiegelung an einer Ebene (die durch den Ursprung geht) mit dem normierten Normalenvektor ${\vec {n}}$ gilt:

$A_{S_{E}}=E-2A_{P_{n}}$ .

Drehung

Wenn man im dreidimensionalen Raum um eine Ursprungsgerade mit normiertem Richtungsvektor ${\vec {n}}$ dreht, lässt sich die hierfür nötige Drehmatrix folgendermaßen darstellen:

$A_{D}=A_{P_{n}}\ \left(1-\cos \alpha \right)+E\cos \alpha +{\begin{pmatrix}0&-n_{3}&n_{2}\\n_{3}&0&-n_{1}\\-n_{2}&n_{1}&0\end{pmatrix}}\sin \alpha$ ,

wobei wieder die Einheitsmatrix und $\alpha$ den Drehwinkel bezeichnet.

Basierend auf einem Artikel in:

Wikipedia.de