Erklärte Quadratsumme

Diese Grafik zeigt die Quadratsummenzerlegung, d.h. die Zerlegung der totalen Quadratsumme in die erklärte Quadratsumme und die Residuenquadratsumme. Die Summe der grünen Abweichungsquadrate ist die erklärte Quadratsumme.

In der Statistik ist die (durch die Regression) erklärte Quadratsumme, bzw. erklärte Abweichungsquadratsumme, kurz SQE für Summe der Quadrate der Erklärten Abweichungen (englisch sum of squared explained deviations, kurz SSE oder explained sum of squares, kurz ESS), Summe der Abweichungsquadrate der ${\hat {y}}$ -Werte, kurz $SAQ_{\hat {y}}$ , bzw. SAQ_Erklärt, oft auch Modellquadratsumme oder Regressionsquadratsumme, die Quadratsumme der Schätzwerte bzw. Regresswerte. Sie wird berechnet als Summe der Quadrate der zentrierten Schätzwerte und kann als „Gesamtvariation der Schätzwerte $\{{\hat {y}}_{i}\}$ “ („erklärte Variation“) interpretiert werden. Über die genaue Bezeichnung und ihre Abkürzungen gibt es international keine Einigkeit. In der deutschsprachigen Literatur wird manchmal die deutsche Bezeichnung mit englischen Abkürzungen gebraucht.

Definition

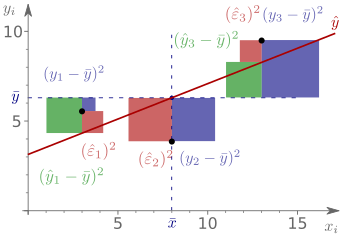
Die erklärte (Abweichungs-)Quadratsumme bzw. Regressionsquadratsumme ist definiert als Quadratsumme der durch die Regressionsfunktion erklärten Abweichungen $({\hat {y}}_{i}-{\overline {y}})$ :

$SQE=SQ_{\mathrm {Erkl{\ddot {a}}rt} }\equiv \sum _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}=\sum _{i=1}^{n}({\hat {y}}_{i}-{\overline {\hat {y}}})^{2}$

Manchmal findet sich auch die Abkürzung $SQR$ bzw. $SQ_{\text{Regression}}$ . Dieser Ausdruck, kann allerdings leicht mit der „Residuenquadratsumme“ (englisch sum of squared residuals) verwechselt werden, die ebenfalls mit $SQR$ abgekürzt wird.

Wenn das zugrundeliegende lineare Modell ein von Null verschiedenes Absolutglied $\beta _{0}$ enthält, stimmt der empirische Mittelwert der Schätzwerte $\hat{y}_i$ mit dem der beobachteten Messwerte $y_{i}$ überein, also $\textstyle {\overline {\hat {y}}}={\tfrac {1}{n}}\sum \nolimits _{i=1}^{n}{\hat {y_{i}}}={\overline {y}}$ (für einen Beweis im multiplen Fall siehe Bestimmtheitsmaß#Matrixschreibweise). Die erklärte Quadratsumme misst die Streuung der Schätzwerte $\hat{y}_i$ um ihren Mittelwert ${\overline {\hat {y}}}={\overline {y}}$ . Das Verhältnis der durch die Regression erklärten Quadratsumme zur totalen Quadratsumme wird Bestimmtheitsmaß der Regression genannt.

Einfache lineare Regression

In der einfachen linearen Regression (Modell mit nur einer erklärenden Variable) $y_{i}=\beta _{0}+x_{i}\beta _{1}+\varepsilon _{i}$ lässt sich die erklärte Quadratsumme auch wie folgt ausdrücken:

$SQE=\sum _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}=\sum _{i=1}^{n}({\hat {y}}_{i}-({\hat {\beta }}_{0}+{\hat {\beta }}_{1}{\overline {x}}))^{2}$ .

Hierbei stellen die ${\hat {y}}_{i}={\hat {\beta }}_{0}+{\hat {\beta }}_{1}x$ die vorhergesagten Werte dar und ${\hat {\beta }}_{0}$ ist die Schätzung des Absolutglieds und ${\hat {\beta }}_{1}$ die Schätzung des Steigungsparameters. Aus dieser Schreibweise lässt sich erkennen, dass sich die erklärte Quadratsumme auch darstellen lässt als Produkt aus dem Quadrat des Bravais-Pearson-Korrelationskoeffizienten $r_{xy}^{2}$ und der totalen Quadratsumme $SQT$ :

$SQE=SQT\cdot r_{xy}^{2}$ ,

wobei ${\hat {\beta }}_{1}$ der Kleinste-Quadrate-Schätzer für die Steigung ${\hat {\beta }}_{1}=SP_{xy}/SQ_{x}$ der Quotient aus Produktsumme von und und Quadratsumme von ist. Um dies zu zeigen, muss zunächst gezeigt werden, dass wenn das zugrundeliegende lineare Modell ein von Null verschiedenes Absolutglied $\beta _{0}$ enthält, der empirische Mittelwert der Schätzwerte $\hat{y}_i$ mit dem der beobachteten Messwerte $y_{i}$ übereinstimmt. Dies gilt, wegen

${\overline {\hat {y}}}={\frac {1}{n}}\sum _{i=1}^{n}{\hat {y_{i}}}={\frac {1}{n}}\sum _{i=1}^{n}({\hat {\beta }}_{0}+{\hat {\beta }}_{1}x_{i})={\hat {\beta }}_{0}+{\hat {\beta }}_{1}{\overline {x}}={\overline {y}}-{\hat {\beta }}_{1}{\overline {x}}+{\hat {\beta }}_{1}{\overline {x}}={\overline {y}}$

und daher

${\begin{aligned}SQE&=\sum \nolimits _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}=\displaystyle \sum \nolimits _{i=1}^{n}({\hat {y}}_{i}-{\overline {\hat {y}}})^{2}\\&=\displaystyle \sum \nolimits _{i=1}^{n}(({\hat {\beta }}_{0}+{\hat {\beta }}_{1}x_{i})-({\hat {\beta }}_{0}+{\hat {\beta }}_{1}{\overline {x}}))^{2}\\&=\displaystyle \sum \nolimits _{i=1}^{n}({\hat {\beta }}_{1}(x_{i}-{\overline {x}}))^{2}\\&={\hat {\beta }}_{1}^{2}\displaystyle \sum \nolimits _{i=1}^{n}\left(x_{i}-{\overline {x}}\right)^{2}\\&={\hat {\beta }}_{1}^{2}SQ_{x}\\&=SQT\cdot r_{xy}^{2}\end{aligned}}$ ,

wobei der letzte Schritt aus der Tatsache folgt, dass sich ${\hat {\beta }}_{1}$ auch schreiben lässt als:

${\hat {\beta }}_{1}={\frac {{\sqrt {\displaystyle \sum \nolimits _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}}{\sqrt {\displaystyle \sum \nolimits _{i=1}^{n}\left(y_{i}-{\bar {y}}\right)^{2}}}}{\displaystyle \sum \nolimits _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}}r_{xy}$ .

Durch die Quadratsummenzerlegung $SQT=SQE+SQR$ bzw. $SQE=SQT-SQR$ kann man durch ersetzen von $SQE=SQT-SQR$ in $SQE=SQT\cdot r_{xy}^{2}$ auf diesem Wege ebenfalls die Folgende Darstellung für die Residuenquadratsumme $SQR$ finden:

$SQR=SQT\cdot (1-r_{xy}^{2})$ .

Matrixschreibweise

In Matrixschreibweise kann die erklärte Quadratsumme wie folgt ausgedrückt werden

$SQE=\left({\hat {\mathbf {y} }}-{\overline {\mathbf {y} }}\right)^{\top }\left({\hat {\mathbf {y} }}-{\overline {\mathbf {y} }}\right)={\hat {\mathbf {y} }}^{\top }{\hat {\mathbf {y} }}-n{\overline {\hat {y}}}^{2}=\mathbf {b} ^{\top }\mathbf {X} ^{\top }\mathbf {y} -n{\overline {y}}^{2}$ .

Hierbei ist ${\overline {\mathbf {y} }}$ ein Vektor mit den Elementen $\overline y$ und ${\hat {\mathbf {y} }}$ ist definiert durch ${\hat {\mathbf {y} }}=\mathbf {X} \mathbf {b}$ , wobei $\mathbf {b} =\left(\mathbf {X} ^{\top }\mathbf {X} \right)^{-1}\mathbf {X} ^{\top }\mathbf {y}$ den Kleinste-Quadrate-Schätzvektor und ${\mathbf {X}}$ die Datenmatrix darstellt.

Literatur

Moosmüller, Gertrud. Methoden der empirischen Wirtschaftsforschung. Pearson Deutschland GmbH, 2008.
Ludwig Fahrmeir, Rita Künstler, Iris Pigeot, Gerhard Tutz: Statistik. Der Weg zur Datenanalyse. 8., überarb. und erg. Auflage. Springer Spektrum, Berlin/ Heidelberg 2016, ISBN 978-3-662-50371-3.

Basierend auf einem Artikel in:

Wikipedia.de