Cramér-Rao-Ungleichung

Illustration der Cramer-Rao Schranke: es gibt keinen unberührten Schätzer, welcher den (2-dimensionalen) Parameter mit niedrigerer Varianz schätzt als die Cramer-Rao Schranke, welche als Standardabweichungs-Ellipse dargestellt ist

Die Cramér-Rao-Ungleichung, auch Informationsungleichung oder Fréchet-Ungleichung genannt, ist eine zentrale Ungleichung der Schätztheorie, einem Teilgebiet der mathematischen Statistik. Sie liefert in regulären statistischen Modellen eine Abschätzung für die Varianz von Punktschätzern und damit eine Möglichkeit, unterschiedliche Schätzer miteinander zu vergleichen sowie ein Kriterium für die Bestimmung von gleichmäßig besten erwartungstreuen Schätzern.

Die Ungleichung ist nach Harald Cramér und Calyampudi Radhakrishna Rao beziehungsweise nach Maurice René Fréchet benannt.

Aussage

Rahmenbedingungen

Gegeben sei ein einparametriges Standardmodell $(X,{\mathcal {A}},(P_{\vartheta })_{\vartheta \in \Theta })$ , das heißt, es ist $\Theta \subset \mathbb {R}$ und jedes der $P_{\vartheta }$ besitzt eine Dichtefunktion $f(x,\vartheta )$ bezüglich des Maßes $\mu$ .

Des Weiteren seien die Cramér-Rao-Regularitätsbedingungen erfüllt, das heißt, es gilt:

$\Theta$ ist eine offene Menge.
Die Dichtefunktion $f(x,\vartheta )$ ist auf ganz $X\times \Theta$ echt größer als 0.
Die Score-Funktion

$S_{\vartheta }(x)={\frac {\partial }{\partial \vartheta }}\ln f(x,\vartheta )$

existiert und ist endlich.

Die Fisher-Information $I(\vartheta )$ ist echt positiv und endlich.
Es gilt die Vertauschungsrelation

$\int {\frac {\partial }{\partial \vartheta }}f(x,\vartheta )\mathrm {d} \mu (x)={\frac {\partial }{\partial \vartheta }}\int f(x,\vartheta )\mathrm {d} \mu (x)$ .

Formulierung

Ist dann $T$ ein Schätzer mit endlicher Varianz und ist

$\operatorname {E} _{\vartheta }(T):=g(\vartheta )\quad \mathrm {f{\ddot {u}}r\;alle\;} \vartheta \in \Theta$

so ist $T$ ein erwartungstreuer Schätzer für $g$ . Ist nun $T$ ein regulärer Schätzer in dem Sinne, als dass die Vertauschungsrelation

${\frac {\partial }{\partial \vartheta }}\int T(x)\cdot f(x,\vartheta )\,\mathrm {d} \mu (x)=\int T(x)\cdot {\frac {\partial }{\partial \vartheta }}f(x,\vartheta )\,\mathrm {d} \mu (x)$ ,

gültig ist, so gilt die Cramér-Rao-Ungleichung

$\operatorname {Var} _{\vartheta }(T)\geq {\frac {\left[g'(\vartheta )\right]^{2}}{I(\vartheta )}}\quad \mathrm {f{\ddot {u}}r\;alle\;} \vartheta \in \Theta$

wobei $g'(\vartheta )$ die Ableitung von $g(\vartheta )$ ist.

Bemerkungen

Die Definition der zu schätzenden Funktion $g$ über den Erwartungswert von $T$ garantiert die Differenzierbarkeit dieser Funktion. Alternativ kann auch $T$ als ein erwartungstreuer Schätzer für eine differenzierbare Funktion $g$ definiert werden.

Formulierung für verzerrte Schätzer

Für verzerrte Schätzer mit Verzerrung $b(\theta )=E[{\hat {\theta }}]-\theta$ gilt: $\operatorname {E} \left(({\hat {\theta }}-\theta )^{2}\right)\geq {\frac {[1+b'(\theta )]^{2}}{I(\theta )}}+b(\theta )^{2},$ wobei $b'(\theta )$ kleiner Null sein kann und somit die Varianz im Vergleich zu einem unverzerrten Schätzer verkleinern kann.

Abgeleitete Begriffe

Cramér-Rao-Schranke

Ist $T$ ein erwartungstreuer Schätzer für die Funktion $g(\vartheta )=\vartheta$ , so vereinfacht sich die Cramér-Rao-Ungleichung zu

$\operatorname {Var} _{\vartheta }(T)\geq {\frac {1}{I(\vartheta )}}\quad \mathrm {f{\ddot {u}}r\;alle\;} \vartheta \in \Theta$ .

Dies nennt man auch die Cramér-Rao-Schranke.

Cramér-Rao-Effizienz und Supereffizenz

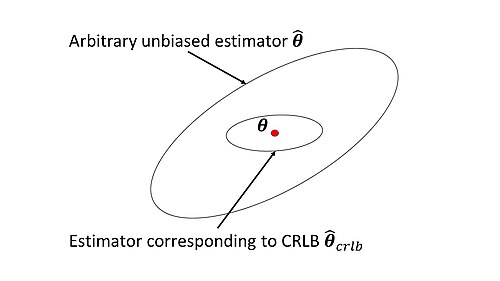
Ein Schätzer, welcher die Cramér-Rao-Ungleichung mit Gleichheit erfüllt, heißt ein Cramér-Rao-effizienter Schätzer. Er ist ein gleichmäßig bester erwartungstreuer Schätzer für die Klasse der regulären Schätzer, also diejenigen, für die die obige Vertauschungsrelation gilt. Einfachstes und bekanntestes Beispiel eines Cramér-Rao-effizienter Schätzers ist das arithmetische Mittel ${\overline {X}}$ als Schätzer für den Erwartungswert $\mu$ einer Normalverteilung.

Schätzer, die die Cramér-Rao-Ungleichung sogar unterschreiten, werden supereffizient genannt. Diese sind notwendigerweise nicht-regulär oder nicht-erwartungstreu, erfüllen also nicht die Bedingungen der Cramér-Rao-Ungleichung. Der bekannteste Vertreter supereffizienter Schätzer ist der James-Stein-Schätzer.

Regularitätsbedingungen und Beweisidee

Der Beweis der Cramér-Rao-Ungleichung beruht im Wesentlichen auf der Cauchy-Schwarz-Ungleichung und zwei Modellannahmen, die die Vertauschbarkeit von Differentiation und Integration regeln.

Einerseits soll

$\mathrm {E} _{\vartheta }\left[{\frac {\partial }{\partial \vartheta }}\log f_{\vartheta }(X_{i})\right]=0$

gelten und andererseits nehmen wir

$\mathrm {E} _{\vartheta }\left[T(X){\frac {\partial }{\partial \vartheta }}\log f_{\vartheta }(X_{i})\right]={\frac {\partial }{\partial \vartheta }}\mathrm {E} _{\vartheta }\left[T(X)\right]$

an. Direktes Einsetzen in die Cauchy-Schwarz-Ungleichung liefert dann die Behauptung.

Mehrdimensionale Formulierung

Unter ähnlichen Regularitätsbedingungen ist die Cramér-Rao-Ungleichung auch im Falle mehrdimensionaler Parameter formulierbar. Die Aussage überträgt sich dann auf die Betrachtung der Kovarianzmatrix des mehrdimensionalen Schätzers und liefert eine $\leq$ -Relation im Sinne der Löwner-Halbordnung für Matrizen.

Sei ${\underline {\vartheta }}:=\left[\vartheta _{1},\vartheta _{2},...,\vartheta _{n}\right]^{T}$ der Vektor der unbekannten Parameter und $\mathbf {X}$ eine multivariate Zufallsvariable mit zugehöriger Wahrscheinlichkeitsdichte $f(\mathbf {X} ;{\underline {\vartheta }})$ .

Der Schätzer

${\underline {T}}(\mathbf {X} ):=\left[T_{1}(\mathbf {X} ),T_{2}(\mathbf {X} ),...,T_{n}(\mathbf {X} )\right]^{T}$

für den Parametervektor ${\underline {\vartheta }}$ besitzt eine Kovarianzmatrix

$\mathrm {Cov} [{\underline {T}}(\mathbf {X} )]=\mathrm {E} [({\underline {T}}(\mathbf {X} )-{\underline {\vartheta }})({\underline {T}}(\mathbf {X} )-{\underline {\vartheta }})^{T}]$ .

Die Cramér-Rao-Ungleichung lautet in diesem Fall

$\mathrm {Cov} [{\underline {T}}(\mathbf {X} )]\geq {\mathcal {I}}^{-1}({\underline {\vartheta }})$

wobei ${\mathcal {I}}$ die Fisher-Informationsmatrix

${\mathcal {I}}_{ij}({\underline {\vartheta }})=\mathrm {E} \left[{\frac {\partial }{\partial \vartheta _{i}}}\log \prod _{\ell =1}^{n}f(X_{\ell };{\underline {\vartheta }}){\frac {\partial }{\partial \vartheta _{j}}}\log \prod _{\ell =1}^{n}f(X_{\ell };{\underline {\vartheta }})\right]$

ist.

Anwendungen

Mit Hilfe der Cramér-Rao-Ungleichung lässt sich die dynamische Permeabilitätszahl von Membranen abschätzen, was vor allem in der Bio- und Nanotechnologie rege Anwendung findet.

Verallgemeinerungen

Eine mögliche Verallgemeinerung ist die Chapman-Robbins-Ungleichung. Sie erlaubt eine Abschätzung der Varianz eines Schätzers bezüglich eines fest vorgegebenen $P_{\vartheta _{0}}$ und wird daher für Abschätzungen im Rahmen der Untersuchung von lokal minimalen Schätzern verwendet. Bei Grenzübergang liefert sie eine punktweise Version der Cramér-Rao-Ungleichung.

Als eine Verallgemeinerung der Cramér-Rao-Ungleichung kann auch die Van-Trees-Ungleichung aus der bayesschen Statistik angesehen werden. Im Unterschied zu dieser lässt sich die Van-Trees-Ungleichung auch auf nicht-erwartungstreue Schätzer anwenden.

Siehe auch

Konsistente Schätzfolge

Weblinks

M.S. Nikulin: Rao-Cramér inequality. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und European Mathematical Society Press, Berlin 2002, ISBN 1-55608-010-7 (englisch, encyclopediaofmath.org).

Literatur

Ludger Rüschendorf: Mathematische Statistik. Springer Verlag, Berlin Heidelberg 2014, ISBN 978-3-642-41996-6, doi: 10.1007/978-3-642-41997-3.
Claudia Czado, Thorsten Schmidt: Mathematische Statistik. Springer-Verlag, Berlin Heidelberg 2011, ISBN 978-3-642-17260-1, doi: 10.1007/978-3-642-17261-8.
Hans-Otto Georgii: Stochastik. Einführung in die Wahrscheinlichkeitstheorie und Statistik. 4. Auflage. Walter de Gruyter, Berlin 2009, ISBN 978-3-11-021526-7, doi: 10.1515/9783110215274.
Helmut Pruscha: Vorlesungen über Mathematische Statistik. B. G. Teubner, Stuttgart 2000, ISBN 3-519-02393-8, Abschnitt V.1.
Posterior uncertainty, asymptotic law and Cramér-Rao bound, Structural Control and Health Monitoring 25(1851):e2113 DOI:10.1002/stc.2113

Basierend auf einem Artikel in:

Wikipedia.de