
Lévyprozess
Lévyprozesse, benannt nach dem französischen Mathematiker Paul Lévy (1886–1971), sind stochastische Prozesse mit stationären, unabhängigen Zuwächsen. Sie beschreiben die zeitliche Entwicklung von Größen, die zwar zufälligen, aber über die Zeit (in Verteilung) gleich bleibenden und voneinander unabhängigen Einflüssen ausgesetzt sind. Viele wichtige Prozesse, wie der Wienerprozess oder der Poissonprozess, sind Lévyprozesse.
Definition
Sei
ein stochastischer Prozess über der Indexmenge
(meist
oder
).
Man sagt,
habe unabhängige Zuwächse, wenn für alle
die Zufallsvariablen
(die Zuwächse von
)
unabhängig
sind.
Ist die Verteilung der Zuwächse über gleich langen Zeitintervallen dieselbe, d.h. gilt
so nennt man
einen Prozess
mit stationären Zuwächsen.
Als Lévyprozesse bezeichnet man genau jene Prozesse ,
die unabhängige und stationäre Zuwächse aufweisen. Häufig wird zusätzlich noch
verlangt, dass (fast
sicher)
gilt. Ist >
ein allgemeiner Lévyprozess, dann wird durch
ein Lévyprozess
mit
definiert. Im Folgenden sei stets
vorausgesetzt.
Zeitdiskrete Lévyprozesse
Gilt speziell ,
so lässt sich die Klasse der Lévyprozesse sehr einfach charakterisieren: Es gibt
nämlich für alle solchen Prozesse
eine Darstellung
wobei
unabhängige und identisch verteilte Zufallsvariablen sind. Andererseits ist für
jede Folge von unabhängigen Zufallsvariablen
,
die alle die gleiche beliebig vorgegebene Verteilung haben, durch
und
ein Lévyprozess X definiert. Im zeitdiskreten Fall ist ein Lévyprozess also im
Prinzip nichts anderes als ein Random
Walk mit beliebiger, aber gleich bleibender Sprungverteilung. Das einfachste
Beispiel für einen zeitdiskreten Lévyprozess ist demnach auch der einfache,
symmetrische Random Walk, bei dem
symmetrisch bernoulliverteilt
ist. Hier bewegt sich der Prozess X, startend bei
,
in jedem Schritt mit Wahrscheinlichkeit ½ um Eins nach oben, andernfalls um Eins
nach unten.
Zeitstetige Lévyprozesse
Im Fall
ist die Charakterisierung nicht mehr so leicht: So gibt es zum Beispiel keinen
zeitstetigen Lévyprozess, bei dem
wie oben bernoulliverteilt ist.
Jedoch sind zeitstetige Lévyprozesse eng verwandt mit dem Begriff der unendlichen
Teilbarkeit: Ist nämlich
ein Lévyprozess, so ist
unendlich teilbar. Andererseits legt eine unendlich teilbare Zufallsvariable
bereits die Verteilung des gesamten Lévyprozesses
eindeutig fest. Jedem Lévyprozess entspricht also eine unendlich teilbare
Verteilungsfunktion und umgekehrt.
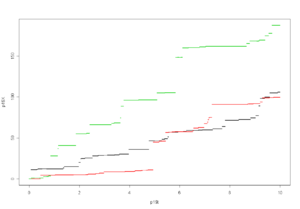
Wichtige Beispiele für zeitstetige Lévyprozesse sind der Wienerprozess (auch
Brownsche Bewegung genannt), bei dem die unendlich teilbare Verteilung von
eine Normalverteilung
ist, oder der Poissonprozess,
bei dem die
poissonverteilt
ist. Doch auch viele andere Verteilungen, beispielsweise die Gammaverteilung oder
die Cauchyverteilung,
können zur Konstruktion von Lévyprozessen herangezogen werden. Neben dem
deterministischen Prozess
ist der Wienerprozess mit konstanter Drift und konstanter Volatilität der
einzige stetige Lévyprozess, d.h. aus der Stetigkeit eines Lévyprozesses
folgt schon die Normalverteilung seiner Zuwächse. Es existiert jedoch
beispielsweise kein Lévyprozess mit gleichverteilten
Zuständen.
Wichtig ist auch der Begriff der endlichen und unendlichen Aktivität: Gibt es in einem Intervall unendlich viele (und damit unendlich kleine) Sprünge oder nicht? Auskunft darüber gibt auch das Lévymaß.
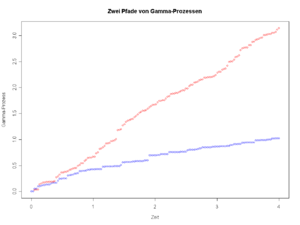
Weiterhin sind Subordinatoren von Bedeutung, das sind Lévyprozesse mit fast sicher monoton wachsenden Pfaden. Ein Beispiel dafür ist der Gamma-Prozess. Die Differenz von zwei Gamma-Prozessen wird als variance-gamma-process bezeichnet.
Weitere Definition
Ein stochastischer Prozess
über einem Wahrscheinlichkeitsraum
heißt Lévyprozess, wenn
,
unabhängige und stationäre Zuwächse hat und
stochastisch stetig ist, d.h. für beliebige
und
gilt
.
Lévy-Chintschin-Formel
Für jeden -wertigen
Lévyprozess
lässt sich seine charakteristische
Funktion schreiben in der Form:
mit dem charakteristischen Exponenten
und dem charakteristischen Tripel .
Dabei ist
eine symmetrische
positiv
definite Matrix,
ein Vektor und
ein Maß auf
mit
und
Das charakteristische Tripel ist durch den Prozess eindeutig bestimmt.
Benannt ist diese Darstellung der charakteristischen Funktion eines Lévyprozesses nach Paul Lévy und Alexandr Chintschin.
Lévy-Itō-Zerlegung
Jeder Lévyprozess kann als eine Summe aus einer brownschen Bewegung, einem linearen Driftprozess und einem reinen Sprungprozess, welcher alle Sprünge des ursprünglichen Lévyprozesses beinhaltet, dargestellt werden. Diese Aussage ist bekannt als Lévy-Itō-Zerlegung.
Sei
ein Lévyprozess in
mit charakteristischem Tripel
.
Dann gibt es drei unabhängige Lévyprozesse, die alle auf dem gleichen
Wahrscheinlichkeitsraum definiert sind,
,
,
,
so dass:
ist eine brownsche Bewegung mit Drift, also ein Lévyprozess mit charakteristischem Tripel
;
ist ein Lévyprozess mit charakteristischem Tripel
(also ein Compound-Poissonprozess);
ist ein quadratintegrierbares Martingal und ein reiner Sprungprozess mit dem charakteristischen Tripel
.
Wichtige Eigenschaften
- Die Erwartungswertfunktion
eines Lévyprozesses
ist linear in t, d.h.
-
. Analog gilt für die Varianz
(vorausgesetzt die entsprechenden Momente existieren zum Zeitpunkt 1). Für die Kovarianzfunktion gilt
.
- Falls
gilt, so ist
ein Martingal.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 08.12. 2020