Sorgenfrey-Ebene

Die Sorgenfrey-Ebene ist ein nach dem Mathematiker Robert Henry Sorgenfrey benanntes Beispiel aus dem mathematischen Teilgebiet der Topologie.

Definition

Ist die Sorgenfrey-Gerade, so heißt das kartesische Produkt $R^2 = R\times R$ mit der Produkttopologie die Sorgenfrey-Ebene. Dabei ist die Sorgenfrey-Gerade derjenige topologische Raum, der auf der Menge $\mathbb {R}$ von allen halboffenen Intervallen [a,b) als Basis erzeugt wird, das heißt die offenen Mengen dieses Raums sind die als beliebige Vereinigung halboffener Intervalle [a,b) darstellbaren Mengen.

Die der Sorgenfrey-Ebene zugrundeliegende Menge ist also $\mathbb {R} ^{2}$ und die Topologie der Sorgenfrey-Ebene wird demnach von der Menge aller halboffenen Rechtecke der Form $[a,b)\times [c,d)$ als Basis erzeugt.

Beispiele offener Mengen

Da die Mengen [a,b) in der Sorgenfrey-Geraden offen und abgeschlossen sind, gilt das auch für $[a,b)\times [c,d) \subset R^2$ . Die Sorgenfrey-Ebene besitzt daher eine Basis aus offen-abgeschlossenen Mengen.

Jedes bezüglich der euklidischen Topologie offene Rechteck $(a,b)\times(c,d)$ ist auch offen bezüglich der Topologie der Sorgenfrey-Ebene, denn

$(a,b)\times (c,d) = \bigcup_{n=1}^\infty[a+\frac{1}{n},b)\times [c+\frac{1}{n},d)$ .

Die Topologie der Sorgenfrey-Ebene ist daher echt feiner als die euklidische Topologie.

Eigenschaften

Die Sorgenfrey-Ebene $R^{2}$ hat folgende Eigenschaften:

$R^{2}$ ist als Produkt eines vollständig regulären Raumes vollständig regulär.
$R^{2}$ ist total unzusammenhängend.
$R^{2}$ hat die Lebesgue’sche Überdeckungsdimension 0.
$R^{2}$ ist nicht diskret, denn eine einelementige Menge enthält keine Basismenge. Die Topologie der Sorgenfrey-Ebene ist aber echt feiner als die euklidische Topologie auf $\mathbb {R} ^{2}$ .
$R^{2}$ ist separabel ( $\mathbb{Q} ^{2}$ liegt dicht, denn jede Basismenge enthält einen Punkt mit rationalen Koordinaten), genügt dem ersten Abzählbarkeitsaxiom (die Mengen $\textstyle [a,a+{\frac {1}{n}})\times [b,b+{\frac {1}{n}})$ bilden eine Umgebungsbasis von $(a,b)\in R^2$ ), aber nicht dem zweiten Abzählbarkeitsaxiom.
$R^{2}$ ist nicht metrisierbar, denn für metrische Räume folgt aus der Separabilität das zweite Abzählbarkeitsaxiom.
$R^{2}$ ist kein normaler Raum (siehe unten).

Gegenbeispiele

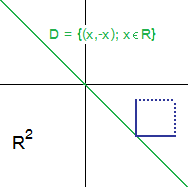
Der Unterraum trägt die diskrete Topologie.

Die Menge $D:=\{(x,-x); x\in R\}\subset R^2$ trägt als Teilraumtopologie die diskrete Topologie, denn für jeden Punkt $(x,-x)\in D$ gilt $\{(x,-x)\} = D\cap [x,x+1)\times [-x,-x+1)$ , wie nebenstehende Zeichnung verdeutlicht.

Insbesondere ist mit der Teilraumtopologie nicht separabel. Die Sorgenfrey-Ebene ist daher ein Beispiel dafür, dass sich Separabilität im Allgemeinen nicht auf Teilräume vererbt. Ein weiteres Beispiel für diesen Sachverhalt ist der Niemytzki-Raum.

als Teilmenge von $R^{2}$ ist abgeschlossen, da schon bezüglich der euklidischen Topologie abgeschlossen ist. Wegen der Diskretheit von ist dann jede Teilmenge von abgeschlossen in $R^{2}$ . Setzt man $E:=\{(x,-x); x\in \Q\}\subset R^2$ , so sind und $D\setminus E$ zwei disjunkte, abgeschlossene Mengen, die sich nicht durch offene Mengen trennen lassen. $R^{2}$ ist daher nicht normal. Da die Sorgenfrey-Gerade normal ist, zeigt die Sorgenfrey-Ebene, dass ein Produkt normaler Räume im Allgemeinen nicht normal ist. Da die Sorgenfrey-Gerade sogar parakompakt ist, ist die Sorgenfrey-Ebene auch ein Beispiel dafür, dass Produkte parakompakter Räume im Allgemeinen nicht wieder parakompakt sind.

Literatur

Johann Cigler, Hans-Christian Reichel: Topologie. Eine Grundvorlesung (= BI-Hochschultaschenbücher. Band 121). Bibliographisches Institut, Mannheim u.a. 1978, ISBN 3-411-00121-6.

Basierend auf einem Artikel in:

Wikipedia.de