Carmichael-Funktion
Die Carmichael-Funktion aus dem
Bereich der Mathematik
ist eine zahlentheoretische
Funktion, die zu jeder natürlichen Zahl n das kleinste
bestimmt, so dass:
für jedes
gilt, das teilerfremd
zu
ist. In gruppentheoretischer
Sprechweise ist
der Gruppenexponent
der (primen)
Restklassengruppe
.
Die Carmichael-Funktion geht auf den Mathematiker Robert Daniel Carmichael zurück. Sie ist die maximale Periodenlänge des Bruches
in seinen
-adischen
Darstellungen und spielt bei Primzahlen
und fermatschen
Pseudoprimzahlen eine Rolle.
Berechnung
Die Carmichael-Funktion lässt sich nach folgendem Schema berechnen:
Dabei stehen die
für paarweise verschiedene Primzahlen und die
für positive ganze Zahlen.
Die folgende Formel kommt zum selben Ergebnis:
Sei
die Primfaktorzerlegung
von
(mit
,
falls
gerade):
falls
falls
Dabei bezeichnet
die Eulersche
φ-Funktion. Für Potenzen ungerader Primzahlen
gilt
Beispiel
gilt für alle
, die teilerfremd zur Zahl 15 sind.
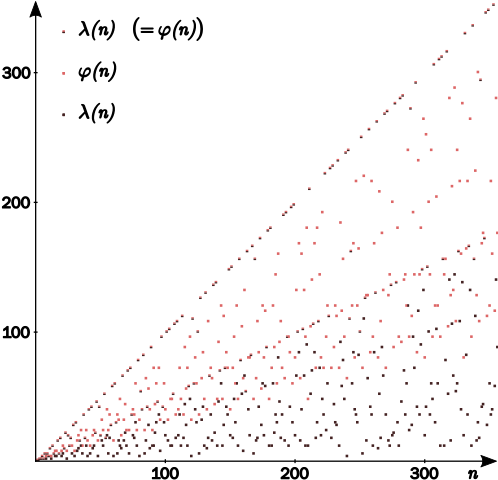
Die Carmichael-Funktion und die eulersche φ-Funktion
Für die Zahlen Eins, Zwei, Vier, für jede ungerade Primzahlpotenz und für
alle Doppelten von ungeraden Primzahlpotenzen sind die Carmichael-Funktion und
die Eulersche
φ-Funktion identisch. Genau dann, wenn ,
existieren auch Primitivwurzeln
modulo
.
Im Allgemeinen unterscheiden sich beide Funktionen;
ist jedoch stets ein Teiler von
.
- Eulersche φ-Funktion:
- Carmichael-Funktion:
Die Carmichael-Funktion und die Carmichael-Zahl
Da die Carmichael-Funktion zu jeder natürlichen Zahl
das kleinste
bestimmt, so dass
für jedes
gilt, das teilerfremd zu
ist, und für jede Carmichael-Zahl
die Differenz
durch
teilbar ist, folgt aus:
auch
.
Für eine Carmichael-Zahl
ist die Zahl
also ganz, und es gilt für alle zu
teilerfremden
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 17.03. 2020