
Indexellipsoid
Das Indexellipsoid, auch Fletcher-Ellipsoid nach Lazarus Fletcher, ist eine Indikatrix zur Beschreibung der Lichtbrechung (genauer: der Brechungsindizes, Einzahl: -index, daher der Name) in einem doppelbrechenden Kristall. Zusammen mit dem Fresnel-Ellipsoid (nach Augustin Jean Fresnel) ermöglicht dieses Ellipsoid eine anschauliche Beschreibung der Ausbreitung von Licht in Materie.
Grundlagen
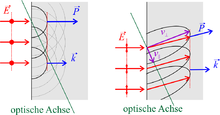
Die Menge aller Punkte, die – von einem punktförmigen Erregungsort ausgehend – gleichzeitig von einer Welle erreicht werden, bilden die Wellenfläche einer Elementarwelle. Das Verhalten einer ebenen Wellenfront kann durch das huygenssche Prinzip erklärt werden:
- Von jedem Punkt der Wellenfront geht eine Elementarwelle aus. Die äußere Einhüllende aller Wellenflächen dieser Elementarwellen bilden die beobachtbare Welle.
In einem optisch isotropen Medium ist die Ausbreitungsgeschwindigkeit des Lichts in allen Richtungen identisch, und die Wellenflächen entsprechen daher Kugelwellen. Auch der Übergang zwischen zwei optisch isotropen Medien kann mit Hilfe des huygensschen Prinzips beschrieben werden und führt auf das snelliussche Brechungsgesetz.
Wird ein Lichtstrahl hingegen auf einen Calcitkristall gerichtet (anisotropes Material), so treten zwei Lichtstrahlen aus. Dieses Phänomen nennt man Doppelbrechung. Während der eine Strahl dem snelliusschen Brechungsgesetz folgt (ordentlicher Strahl), gilt dies für den zweiten nicht (außerordentlicher Strahl). Ursache dafür ist, dass in Calcit die Lichtgeschwindigkeit von der Ausbreitungsrichtung und der Polarisationsrichtung des Lichtstrahls abhängt. Während die Wellenfläche des ordentlichen Strahls weiterhin Kugelwellen sind, sind die Wellenflächen des außerordentlichen Strahls Rotationsellipsoide. Die Form der Wellenfläche kann aus dem Fresnel-Ellipsoid hergeleitet werden (fresnelsche Wellenfläche).
Führt man die huygenssche Konstruktion mit elliptischen Wellen durch, so ergibt sich, dass die Überlagerung der Wellenflächen wieder zu einer ebenen Welle führt. Die Wellenfront dieser ebenen Welle bewegt sich allerdings nicht mehr nur in Richtung ihrer Normalen, sie kann sich auch schräg dazu bewegen: Die Richtung und Geschwindigkeit der Wellennormalen (im Bild: k) und der Strahlrichtung (im Bild: P) stimmen nicht mehr überein.
Für die Wellennormale gilt weiterhin das snelliussche Brechungsgesetz. Für jeden Strahl können die entsprechenden Brechungsindizes mit Hilfe des Indexellipsoids bestimmt werden.
Konstruktion
In einem optisch anisotropen Medium muss der lineare Zusammenhang zwischen
dem elektrischen
Feld
und der dielektrischen
Verschiebung
in richtungsabhängiger Form geschrieben werden, da diese beiden Vektoren im
Allgemeinen nicht mehr parallel zueinander liegen:
wobei die dielektrischen
Konstanten
einen symmetrischen Tensor
2. Stufe bilden.
Entsprechend gilt für den dazu inversen Tensor der dielektrischen Moduln
:
Diese Tensoren haben jeweils drei im Allgemeinen unterschiedliche Eigenwerte, stimmen aber in der Lage ihrer Hauptachsen überein.
In Hauptachsenform haben sie folgende Gestalt:
In ihrem Hauptachsensystem (x, y, z) lassen sich Tensoren
2. Stufe mit den Eigenwerten
als Ellipsoide darstellen:
.
Die Längen der Halbmesser der Hauptachsen des Ellipsoids betragen:
Das Ellipsoid, das den dielektrischen Modul repräsentiert, ist das Indexellipsoid. Aus seinen Eigenwerten lassen sich die Hauptbrechungsindizes wie folgt berechnen:
Fresnel-Ellipsoid
Das Ellipsoid, das den dielektrischen Tensor repräsentiert, ist das Fresnel-Ellipsoid. Aus seinen Eigenwerten lassen sich die Hauptlichtgeschwindigkeiten wie folgt berechnen:
Dabei ist
die Lichtgeschwindigkeit
im Vakuum.
Verwendung
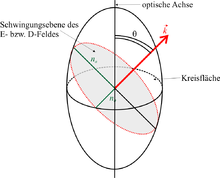
Legt man einen Wellennormalenvektor in den Ursprung des Indexellipsoids, so schneidet die Ebene, die senkrecht zu diesem Vektor steht und durch den Mittelpunkt des Ellipsoids verläuft, das Indexellipsoid so, dass als Schnittlinie eine Ellipse entsteht:
- die Hauptachsen dieser Schnittellipse geben die Richtungen der elektrischen Flussdichte des ordentlichen und des außerordentlichen Strahles an
- die Achsenabschnitte (Halbmesser der Hauptachsen) geben die dazugehörenden Brechungsindizes an.
Ist die Schnittellipse ein Kreis, so bewegen sich alle Wellennormalen unabhängig von der Polarisation der Welle in dieselbe Richtung. Richtungen mit dieser Eigenschaft nennt man optische Achsen.
Fresnel-Ellipsoid
Mit demselben Verfahren kann man für jede Strahlrichtung am Fresnel-Ellipsoid die zugehörige Schnittellipse konstruieren:
- die Hauptachsen dieser Schnittellipse geben die Richtungen des elektrischen Feldes des ordentlichen und des außerordentlichen Strahles an
- die Achsenabschnitte (Halbmesser der Hauptachsen) geben die dazugehörenden Lichtgeschwindigkeiten an.
Trägt man die Halbmesser dieser Ellipse in Strahlrichtung auf und lässt die Strahlrichtung alle Richtungen im Raum einnehmen, so erhält man eine Figur mit zwei Schalen, welche die Wellenfronten des ordentlichen und des außerordentlichen Strahles beschreiben.
Lichtausbreitung in dielektrischen Medien
Nach dem neumannschen Prinzip haben alle Eigenschaftstensoren eine durch das Kristallsystem bestimmte Form. Im Falle von Tensoren 2. Stufe gibt es drei prinzipiell unterschiedliche Formen.
Optisch isotrope Kristalle
In einem kubischen Kristall sind die Eigenwerte aller Tensoren 2. Stufe gleich. Sowohl das Index- als auch das Fresnel-Ellipsoid sind daher Kugeln. Folglich sind die zugehörigen Schnittellipsen für alle Strahl- und Wellennormalenrichtungen Kreise. Die beiden Schalen der Strahlfläche fallen auf eine Kugel zusammen. Daher verhalten sich alle Lichtstrahlen unabhängig von ihrer Richtung und Polarisation identisch: kubische Kristalle sind optisch isotrop.
Optisch einachsige Kristalle
In den wirteligen Kristallsystemen (trigonal, tetragonal und hexagonal) liegt die Hauptachse des Tensors, die auch als optische Achse bezeichnet wird, in Richtung der kristallographischen c-Achse; die beiden anderen Hauptachsen liegen senkrecht zu ihr.
Entsprechend gibt es zwei unterschiedliche Eigenwerte bzw. Hauptbrechindizes:
bzw.
(Index
für extraordinary / außerordentlich)
bzw.
(Index
für ordinary / ordentlich).
- Für
heißt der Kristall optisch negativ, Index- und Fresnel-Ellipsoid sind abgeplattete Rotationsellipsoide.
- für
heißt der Kristall optisch positiv, Index- und Fresnel-Ellipsoid sind verlängerte Rotationsellipsoide.
Zur Beschreibung betrachtet man den Strahl im Hauptschnitt, d.h. in der Ebene, in der sowohl der einfallende Lichtstrahl als auch die optische Achse liegen. Für jede Wellennormalenrichtung liegt eine Halbachse der zugeordneten Schnittellipse in der Hauptebene, die andere senkrecht dazu.
- Die Länge der senkrecht zur Hauptebene stehenden Halbachse ist für alle Richtungen gleich no.
- Die Länge der in der Hauptebene liegenden Halbachse liegt
zwischen no und ne, je nach Winkel der
Wellennormalenrichtung zur optischen Achse, mit den Extremwerten:
- ne für Winkel 90°
- no für Winkel 0°, d.h. wenn die Wellennormale in Richtung der optischen Achse liegt, ist die Schnittellipse ein Kreis, und beide Brechungsindizes sind gleich no.
Die Schnittellipsen des Fresnel-Ellipsoids verhalten sich genauso.
Daher besteht die Wellenfläche aus zwei Schalen:
- einer Kugel mit dem Radius no (die Wellenfront des ordentlichen Strahls ist – unabhängig von der Strahlrichtung – kugelförmig)
- einem Rotationsellipsoid mit Halbachsen der Längen no und ne (Rotationsachse) (die Wellenfront des außerordentlichen Strahls ist ellipsoid).
Dabei liegt, abgesehen von den Berührpunkten, die jeweils auf einem Kreis mit dem Radius no liegen:
- das Ellipsoid vollständig in der Kugel oder
- die Kugel vollständig im Ellipsoid.
Zusammengefasst: Fällt eine ebene Welle auf einen optisch einachsigen Kristall, so entstehen in der Regel zwei Strahlen.
- Einer der beiden Strahlen ist senkrecht zur Hauptebene polarisiert. Bei diesem Strahl stimmen Strahlrichtung und Wellennormalrichtung überein, wie bei den Strahlen in optisch isotropen Medien. Er folgt damit dem snelliusschen Brechungsgesetz. Dieser Strahl wird daher ordentlicher Strahl genannt.
- Der andere Strahl ist in der Hauptebene polarisiert. Bei ihm stimmen Wellennormalrichtung und Strahlrichtung in der Regel nicht überein: Nur die Wellennormalrichtung folgt dem snelliusschen Brechungsgesetz, mit einem richtungsabhängigen Brechungsindex, der vom Brechungsindex des ordentlichen Strahls abweicht. Der Strahl selbst ist aber gegenüber der „normalen“ Brechungsrichtung seitlich verschoben. Dieser Strahl wird daher außerordentlicher Strahl genannt.
- Wird der Lichtstrahl in Richtung der kristallographischen c-Achse eingestrahlt, so verhalten sich ordentlicher und außerordentlicher Strahl identisch: Sie haben den gleichen Brechungsindex no und die gleiche Strahlgeschwindigkeit. Daher wird diese Achse auch optische Achse genannt. In einem optisch einachsigen System ist die optische Achse eine Richtung optischer Isotropie.
Optisch zweiachsige Kristalle
Im orthorhombischen, monoklinen und triklinen Kristallsystem liegen optisch zweiachsige Kristalle vor. Man erhält hier in der Regel zwei Strahlen, die sich wie der außerordentliche Strahl verhalten. Sie können nach demselben Prinzip beschrieben werden, allerdings sind die Verhältnisse deutlich komplizierter. Hier kann daher nur ein Überblick über die wichtigsten Besonderheiten gegeben werden, für weitere Informationen wird auf die Fachliteratur verwiesen.
In optisch zweiachsigen Kristallen gibt es zwei optische Achsen und drei
unterschiedlich große Hauptachsen (x,y,z) bzw. Hauptbrechungsindizes .
Die Hauptachsen werden so gewählt, dass gilt:
Ihre Lage zu den Kristallachsen folgt dem neumannschen Prinzip. Da alle drei Hauptachsen unterschiedlich lang sind, sind in diesen Systemen das Index- und das Fresnel-Ellipsoid jeweils dreiachsig.
Die optischen Achsen findet man folgendermaßen: Dreht man den Wellennormalevektor in der xz-Ebene von der z- in die x-Richtung, so haben alle dabei entstehenden Schnittellipsen eine gemeinsame Hauptachse in y-Richtung mit der Länge nβ. Die zweite Hauptachse liegt in der xz-Ebene und durchläuft alle Werte zwischen nα und nγ. Aufgrund der obigen Definition der Hauptachsen muss es daher eine Richtung geben, bei der auch diese zweite Hauptachse die Länge nβ hat; eine entsprechende Richtung muss es auch zwischen der z- und der x-Richtung geben. Diese beiden Richtungen sind die optischen Achsen oder Binormalen. Der Winkel zwischen den Binormalen wird sowohl von der x- als auch von der z-Achse halbiert.
- Ist der Winkel zwischen der z-Achse und der Binormalen kleiner 45°, so heißt der Kristall optisch zweiachsig positiv
- ist er gleich 45°, so heißt der Kristall optisch zweiachsig neutral
- ist er größer 45°, so heißt der Kristall optisch zweiachsig negativ.
Die Wellenfläche ist eine Fläche 4. Ordnung. Sie ist eine spezielle Form einer kummerschen Fläche. Auch hier gibt es zwei Richtungen, in denen sich die beiden Schalen berühren: die Biradialen. Sie liegen zwar auch in der xz-Ebene, aber nicht in Richtung der Binormalen. Daher ist in einem zweiachsigen System die optische Achse keine Richtung optischer Isotropie. Dies ist die Ursache der konischen Refraktion, die im Folgenden genauer beschrieben wird.
Innere konische Refraktion
Vor eine senkrecht zu einer Binormalen geschnittene Kristallplatte wird eine Blende gestellt, so dass nur ein dünner Lichtstrahl senkrecht zur Platte auf den Kristall fallen kann. Wird der Kristall dann mit einem unpolarisierten Lichtstrahl durchstrahlt, so erkennt man auf einem Schirm hinter dem Kristall einen Ring, dessen Radius sich mit der Entfernung von der Kristallplatte nicht ändert. Zwar bleiben die Wellennormalen alle in Richtung der Binormalen, aber die Wellenfronten verschieben sich- abhängig von ihrer Polarisationsrichtung – senkrecht zur Wellennormalen. Da aber alle Wellennormalen parallel zueinander bleiben, treten alle Strahlen senkrecht zur Kristallfläche aus dem Kristall aus und breiten sich dann auch weiter parallel zueinander aus. Dieser Effekt heißt innere konische Refraktion.
Äußere konische Refraktion
Zwischen zwei Lochblenden wird eine Kristallplatte gestellt, die senkrecht zu einer Biradialen geschnitten ist. Die Blenden sind so angeordnet, dass nur die Lichtstrahlen den Kristall verlassen, die sich im Kristall in Richtung der Biradialen fortbewegt haben. Bestrahlt man die Eintrittsblende so mit divergentem Licht, dass alle möglichen Polarisationsrichtungen durch den Kristall wandern, so erhält man auf einem Schirm hinter dem Kristall ebenfalls wieder einen Kreis, dessen Radius sich mit der Entfernung vom Kristall vergrößert. Ursache dafür ist, dass zwar alle Polarisationsrichtungen dieselbe Strahlgeschwindigkeit haben und sich im Kristall auch in dieselbe Richtung bewegen. Da sie aber unterschiedliche Wellennormalen haben, werden sie an den Kristalloberflächen unterschiedlich gebrochen. Daher muss die Eintrittsblende auch mit divergentem Licht bestrahlt werden. Diesen Effekt nennt man äußere konische Refraktion.
Literatur
- Heinrich Gobrecht (Hrsg.): Bergmann Schaefer Lehrbuch der Experimentalphysik. Band III Optik. 8. Auflage. Walter de Gruyter, Berlin 1987, ISBN 3-11-010882-8.
- Will Kleber, Hans-Joachim Bautsch, Joachim Bohm, Detlef Klimm: Einführung in die Kristallographie. 19. Auflage. Oldenbourg Wissenschaftsverlag, München 2010, ISBN 978-3-486-59075-3.
- D. Schwarzenbach: Kristallographie. Springer, Berlin 2001, ISBN 3-540-67114-5.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 15.01. 2023