
Lorentzkurve
Die Lorentzkurve, nach Hendrik Antoon Lorentz, oder Breit-Wigner-Funktion, nach Gregory Breit und Eugene Wigner, ist eine Kurve, die in der Physik bei der Beschreibung von Resonanzen auftritt.
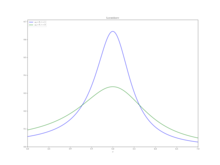
Mathematische Definition und Näherung
In die Breit-Wigner-Funktion gehen zwei Parameter ein. Der Parameter
bestimmt die Position des Maximums,
der Parameter
wird Breite der Kurve genannt. Aus physikalischer Sicht ist eine
Interpretierbarkeit der Kurve nur für
gegeben, da mit
in der Regel eine Kreisfrequenz
assoziiert ist und negative Frequenzen physikalisch unsinnig sind. Die
Funktionsvorschrift lautet:
Eine andere Form der Kurve erhält man durch Reparametrisierung,
indem man statt der Parameter
und
folgenden Satz Parameter verwendet:
Dann ist
;
insbesondere gilt für ,
dass die gestrichenen und ungestrichenen Parameter nahezu identisch werden. Die
erste Form wird für gewöhnlich in der Teilchenphysik
bevorzugt, die zweite Form in der klassischen
Physik, da sie sich in ihren jeweiligen Gebieten aus der Physik in den
entsprechenden Formen ergeben. Zur Rückkonversion dienen die Beziehungen
Entgegen teilweise vertretener Auffassung ist weder
noch
die Halbwertsbreite
(FWHM) der Kurve. Diese ist statt dessen
und ergibt sich für
nur ungefähr zu
.
Für
und
kann die Lorentzkurve durch
approximiert werden. Sie ist dann bis auf einen Normierungsfaktor identisch mit der in der mathematischen Wahrscheinlichkeitstheorie als Cauchy-Verteilung bezeichneten Wahrscheinlichkeitsdichte. Wenn von der Lorentzkurve die Rede ist, ist teilweise auch die approximierte Fassung gemeint.
Physikalische Bedeutung
Klassische Physik
Die Differentialgleichung für den gedämpften harmonischen Oszillator
kann durch Fourier-Transformation in die algebraische Gleichung
überführt werden. Die in diesen Gleichungen auftretende Größen sind:
- die Dämpfungskonstante
- die Resonanzfrequenz
des ungedämpften harmonischen Oszillators
- eine anregende
Funktion
Die Gleichung kann nun elementar gelöst werden, ihre Lösung ist
und ihr Betragsquadrat
die Lorentzkurve in der zweiten Parametrisierung.
Teilchenphysik
In der Teilchenphysik sind die Propagatoren
die Umkehrfunktionen der Bewegungsgleichungen für die Teilchen. Diese haben
einen Pol
bei der Masse
dieser Teilchen. Um dies zu umgehen, führt man eine sogenannte komplexe Masse
ein, die die Zerfallsbreite
des
jeweiligen Teilchens berücksichtigt. Dann ist der Propagator für einen
bestimmten Viererimpuls
proportional zu
und sein Betragsquadrat ist die Lorentzkurve in der ersten Parametrisierung:
Beispiel
Z0-Boson
Speziell für den Zerfall des Z0-Bosons ergibt sich die Breit-Wigner-Formel zu
Hierbei ist
die Partialbreite des Eingangskanals (d.h. für den Zerfall Z0 --> e+ e−)
die Partialbreite des Ausgangskanals
die Summe der Partialbreiten für alle möglichen Zerfälle in Fermion-Antifermion-Paare
die Energie im Schwerpunktssystem
das reduzierte Plancksche Wirkungsquantum
- c die Lichtgeschwindigkeit.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 04.10. 2019