Diode
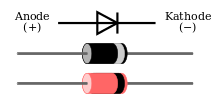


Eine Diode ist ein elektronisches Bauelement, das Strom in einer Richtung passieren lässt und in der anderen Richtung den Stromfluss sperrt. Daher wird von Durchlassrichtung und Sperrrichtung gesprochen. Entdeckt wurde das Verhalten 1874 von Ferdinand Braun an Punktkontakten auf Bleisulfid (Galenit).
Die Bezeichnung Diode wird üblicherweise für Halbleiterdioden verwendet, die mit einem p-n-Übergang oder einem gleichrichtenden Metall-Halbleiter-Übergang (Schottky-Kontakt) arbeiten. In der Halbleitertechnik bezieht sich der Begriff Diode nur auf Siliziumdioden mit p-n-Übergang, während andere Varianten durch Namenszusätze gekennzeichnet werden, beispielsweise Schottky-Diode oder Germaniumdiode. Veraltet sind Bezeichnungen wie Ventilzellen, welche bis Mitte des 20. Jahrhunderts in der damals neu entstandenen Halbleitertechnik für Dioden gebraucht wurden und auf die analoge Funktion eines mechanischen Ventils zurückgehen.
Dioden werden unter anderem zur Gleichrichtung, der Umwandlung von Wechselspannung zu Gleichspannung, eingesetzt. Daneben zeigt der Halbleiterübergang weitere nutzbare Eigenschaften, die z.B. in Zener-, Photo-, Leuchtdioden und Halbleiterdetektoren ausgenutzt werden.
Aufbau und Physik einer Halbleiterdiode

Die Grundlage der Halbleiter-Diode ist entweder ein p-n-dotierter Halbleiterkristall (meist aus Silizium, aber auch Germanium, siehe Germaniumdiode, oder Galliumarsenid) oder ein Metall-Halbleiter-Übergang (siehe Schottky-Diode).
Die Leitfähigkeit eines solchen Übergangs hängt von der Polung der Betriebsspannung an Anode (p-dotiert) und Kathode (n-dotiert), also von der Stromflussrichtung ab. Der p-n-Übergang (graue Fläche) ist eine Zone, die frei von beweglichen Ladungsträgern ist, da positive Ladungsträger (sog. Defektelektronen oder Löcher) des p-dotierten Kristalls und negative Ladungsträger (freie Elektronen) des n-dotierten Kristalls auf die jeweils andere Seite des pn-Übergangs diffundieren und dort durch Rekombination verschwinden (siehe Artikel pn-Übergang). Die ursprünglichen Quellen der Ladungsträger, die Dotierungsatome, sind ortsfest und bilden nun als Ionen eine Raumladung, deren elektrostatisches Feld die beiden Ladungssorten voneinander fernhält und so die weitere Rekombination unterbindet. Über die ganze Raumladungszone hinweg entsteht die Diffusionsspannung. Diese kann durch eine von außen angelegte Spannung – je nach Polung – kompensiert werden, dann wird der p-n-Übergang leitfähig, oder verstärkt werden, dann bleibt er gesperrt.
-
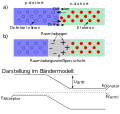 pn-Übergang
pn-Übergang -
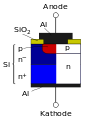 pn-Diode
pn-Diode -
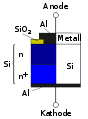 Schottky-Diode
Schottky-Diode
Mechanisches Ersatzmodell der Diode
Die Funktion einer Gleichrichterdiode im Stromkreis kann man sich am
einfachsten wie ein Rückschlagventil
im Wasserkreislauf vorstellen: Wenn ein Druck (eine Spannung) auf dieses Ventil
(Diode) in Sperrrichtung wirkt, wird der Wasser-(Strom-)fluss blockiert. In
Durchlassrichtung muss der Druck (die Spannung) groß genug werden, um die
Federkraft des Ventils (= Schwellen- oder Schleusenspannung der Diode) zu
überwinden. Dadurch öffnet das Ventil (die Diode), und der Strom kann fließen.
Diesem Druck, welcher im mechanischen Modell zum Überwinden der Federkraft
notwendig ist, entspricht bei einer Diode die so genannte Schwellenspannung
()
oder minimale Vorwärtsspannung (engl. forward voltage
drop), die in Flussrichtung an der Diode anliegen muss, damit sie in den
leitenden Zustand übergeht. Bei gewöhnlichen Siliziumdioden liegt
bei ca. 0,6 - 0,7 V.
-
 Geschlossenes Kugelrückschlagventil
Geschlossenes Kugelrückschlagventil -
Geöffnetes Kugelrückschlagventil
-
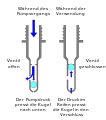 Fahrradventil; der Innendruck wirkt als Rückstellkraft
Fahrradventil; der Innendruck wirkt als Rückstellkraft
Das Rückschlagventil verhält sich wiederum entsprechend der Shockley-Formel, die zur Beschreibung der Halbleiterdiode entwickelt wurde (siehe unten bei Ideale Diode). Die Formel eignet sich daher zur näherungsweisen Berechnung von Ventilen.
Elektrisches Verhalten
Die Analyse elektrischer Schaltungen erfordert eine mathematische Beschreibung der Diode. Hierfür gibt es die grafische Strom-Spannungs-Kennlinie exakte Gleichungen und vereinfachte Modelle.
Formelzeichen
Die detaillierte Betrachtung einer Diode erfordert spezifische Formelzeichen. Die folgende Tabelle erleichtert hierbei die Übersicht.
| Zeichen | Beschreibung |
|---|---|
| Spannung an der Diode | |
| Schleusenspannung (auch Schwellspannung genannt), Diode leitet in Durchlassrichtung | |
| Flussspannung; Spannung an der Diode in Durchlassrichtung (engl. forward voltage);
Entspricht | |
| Sperrspannung;
Spannung an der Diode in Sperrrichtung
(engl. reverse voltage);
Entspricht | |
| Durchbruchspannung (engl. breakdown voltage) | |
| Strom durch die Diode | |
| Sättigungssperrstrom | |
| Diffusionsstrom; Strom durch die Diode in Durchlassrichtung (engl. forward current) | |
| Leckstrom; Strom durch die Diode in Sperrrichtung (engl. reverse current) | |
| Leck-Sättigungssperrstrom | |
| Durchbruchstrom; Strom durch die Diode beim (Rückwärts-)Durchbruch (engl. breakdown current) | |
| Emissionskoeffizient | |
| Temperaturspannung | |
| Bandabstandsspannung (engl. gap voltage) | |
| Bahnwiderstand; ohmscher Widerstand des Halbleitermaterials | |
| Differentieller Widerstand | |
| Arbeitspunkt | |
| Diodenkapazität | |
| Sperrschichtkapazität | |
| Diffusionskapazität |
Zusätzlich sind die folgenden Naturkonstanten wichtig:
| Zeichen | Beschreibung |
|---|---|
| Boltzmannkonstante | |
| Elementarladung |
Statisches Verhalten
Das statische Verhalten beschreibt eine Diode bei Gleichspannung und gilt auch näherungsweise für Wechselspannungen mit niedriger Frequenz, etwa 50 Hz Netzspannung, aber je nach Ausführung auch bis in den MHz-Bereich. Durch eine veränderte Spannung bedingte Umverteilungsvorgänge im p-n-Übergang bleiben unberücksichtigt.
Kennlinie
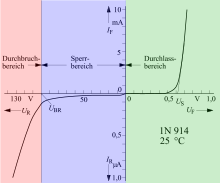
Hinweis: Die Maßstäbe sowohl für die Stromstärke als auch für die Spannung unterscheiden sich um Zehnerpotenzen im Durchlass- und im Sperrbereich
Am anschaulichsten beschreibt die Strom-Spannungs-Kennlinie das statische Verhalten einer Diode. Die Kennlinie teilt sich dabei in drei Abschnitte: den Durchlassbereich, den Sperrbereich und den Durchbruchbereich.
Wie die Kennlinie zeigt, fließt im Durchlassbereich trotz anliegender kleiner
Spannung kein merklicher Strom
durch die Diode (bezogen auf in der Technik übliche Ströme). Erst ab einer
Spannung von etwa 0,4 V beginnt bei Si-Dioden der Strom merklich
anzusteigen. Ab etwa 0,6 V bis 0,7 V nimmt dann der Strom stark zu,
und man spricht deswegen von der Schleusenspannung
.
Bei Schottky- und Germanium-Dioden fließt ein nennenswerter Strom bereits bei
etwa 0,2 V und die Schleusenspannung liegt bei etwa 0,3 V bis
0,4 V.
Im Sperrbereich fließt ein sehr geringer Strom, der sogenannte Leckstrom
.
Dabei weisen Ge- und Schottky-Dioden wesentlich höhere Werte auf als Si-Dioden.
Je nach Dotierung beginnt bei Si-Dioden bei
bzw.
ab etwa −50 V bis −1000 V der Durchbruchbereich und die Diode wird in
Sperrrichtung leitend. Dasselbe gilt für eine Schottky-Diode bei etwa −10 V
bis −200 V. Diese Durchbruchsspannung
wird mit positivem Vorzeichen angegeben. Durch spezielle Dotierungen werden bei
Si-Dioden auch Durchbruchspannungen bis unter 5 V erreicht, was besonders
bei Z-Dioden
angewendet wird.
Ideale Diode / Shockley-Gleichung
Wegen der Nichtlinearität werden Vereinfachungen verwendet, die das Verhalten nur näherungsweise wiedergeben, dabei aber eine leichtere Handhabung ermöglichen. Im einfachen Modell der Diode wird diese als ideales Rückschlagventil angesehen oder als Schalter, dessen Stellung von der Polung der angelegten Spannung abhängt. Die ideale Diode ist in der einen Richtung leitend ohne Spannungsabfall, in der Gegenrichtung sperrend ohne Leckstrom. Damit besteht die Kennlinie aus zwei Halbgeraden auf den Koordinatenachsen. In Gleichungsform wird die ideale Diode beschrieben
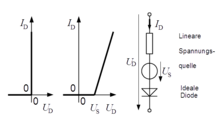
Daneben: Kennlinie des rechtsstehenden Diodenmodells, das eine verbesserte lineare Annäherung an die nichtlineare Kennlinie einer realen Diode ermöglicht
(gilt für 1N4001 bis 1N4007)

-
im Durchlassbereich durch bei im Sperrbereich durch bei
Die Zustände
und
existieren in diesem Modell nicht.
Sollen die Schleusenspannung und der nicht sprunghafte Kennlinienverlauf in die Beschreibung des Verhaltens einbezogen werden wie unten angegeben mit weiterhin linearer Näherung, wird die Ersatzschaltung erweitert gemäß nebenstehendem Bild. Die Richtungen von Stromstärke und Spannung sind so gewählt wie im Verbraucher-Zählpfeilsystem. Bei gleichen Vorzeichen der beiden Größen verhält sich diese Spannungsquelle als Besonderheit wie ein Verbraucher. Dieses zeigt sich in der Erwärmung der realen Diode.
Eine elektronische Schaltung, die beispielsweise zu Messzwecken die Funktion eines Gleichrichters wie eine ideale Diode übernimmt – ohne die Mängel der hohen Schleusenspannung und der nichtlinearen Kennlinie.
Der Wirklichkeit am nächsten kommt die Kennlinie der Diode im Durchlassbereich gemäß der Shockley-Gleichung (benannt nach William Bradford Shockley); sie ist ein Spezialfall der Arrhenius-Gleichung.
- Sättigungssperrstrom
(kurz: Sperrstrom)
- Emissionskoeffizient
- Temperaturspannung
bei Raumtemperatur
- absolute
Temperatur
- Boltzmannkonstante
- Elementarladung
- Sättigungssperrstrom
(kurz: Sperrstrom)
Bei
entsteht ein relativer Fehler
von < 1 %, wenn in der Klammer der zweite Summand weggelassen wird.
Dann gilt
und die Kennlinie nach Shockley wird in einfach logarithmischer Darstellung eine Gerade.
Bei genauerer Betrachtung setzt sich der Diodenstrom aus dem
Diffusionsstrom
unter Berücksichtigung des Hochstromeffekts, dem Leckstrom
und dem Durchbruchsstrom
zusammen:
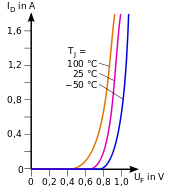
Temperaturabhängigkeit
Die Diodenkennlinie variiert mit der Temperatur. In der Shockley-Gleichung sind zwei temperaturabhängige Terme enthalten:
Dabei sind
der bei der Temperatur
als bekannt vorausgesetzte Sperrstrom,
die Bandabstandsspannung (gap voltage).
Für Silizium
gilt .
Diese Spannung dient (oft temperaturkompensiert) in der Bandabstandsreferenzschaltung
zur Erzeugung von Referenzspannungen.
Zusätzlich muss man auch die Temperaturabhängigkeit der Spannung berücksichtigen:
Dieser Temperaturkoeffizient ist im relevanten Temperaturbereich um 300 K konstant genug, um damit anhand der etwa linearen Temperaturabhängigkeit der Flussspannung Temperaturmessungen vornehmen zu können.
Die Spannung von etwa 0,7 V kann in der Praxis tatsächlich für viele Überschlagsrechnungen als Wert der Flussspannung von Siliziumdioden und p-n-Übergängen angesetzt werden.
Diffusionsstrom
Der Diffusionsstrom tritt im mittleren Durchlassbereich auf, wo er über die anderen Effekte dominiert. Die Formel ergibt sich aus der Shockley-Gleichung mit:
Bei Schottky-Dioden kann mit derselben Formel der Emissionsstrom beschrieben werden.
Hochstromeffekt
Der Hochstromeffekt bewirkt eine Zunahme von
im Bereich der mittleren Ströme auf
bei
für
gegen unendlich. Hierbei beschreibt der Kniestrom
die Grenze zum Hochstrombereich. Es fließt dadurch weniger Strom, und die
Kennlinie besitzt einen flacheren, aber weiterhin exponentiellen Verlauf.
Leckstrom (Rekombinationsstrom)
Beim Anlegen einer Sperrspannung
werden die Elektronen und Löcher zu den jeweiligen Kontakten abgeführt, damit
vergrößert sich die Raumladungszone und die Diode sollte keinen Strom leiten. In
der Praxis misst man aber weiterhin einen geringen Strom, den sogenannten
Leckstrom (Sperrstrom). Er resultiert aus der Diffusion von Ladungsträgern durch
die Raumladungszone in den entgegengesetzt dotierten Bereich, wo sie dann
aufgrund der angelegten Spannung abgeführt werden. Hierbei liefert die p-Zone
Elektronen und die n-Zone Löcher, welche als Minoritätsladungsträger zum
Sperrstrom führen.
Für die mathematische Berechnung gilt:
mit
– Leck-Sättigungssperrstrom
– Emissionskoeffizient in Sperrrichtung
– Diffusionsspannung
– Kapazitätskoeffizient
Der Sperrstrom ist stark spannungs- und temperaturabhängig und hängt von der Herstellungstechnologie sowie Reinheit und Störstellenarmut ab.
Durchbruch
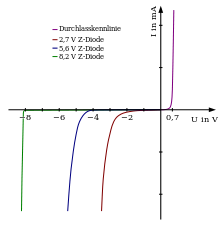
Der Sperrstrom einer pn-Diode in Sperrpolung ist im Allgemeinen gering.
Vergrößert man jedoch die Spannung in Sperrrichtung
weiter, so steigt der Sperrstrom
ab einer bestimmten Sperrspannung zunächst langsam und dann schlagartig an.
Diese Zunahme des Sperrstroms (reverse current) nennt man
allgemein „Durchbruch“, und die zugehörige Spannung wird als Durchbruchspannung
bezeichnet. Die Durchbruchspannung einer Diode hängt allgemein vom
Halbleitermaterial und der Dotierung ab und kann für Gleichrichterdioden im
Bereich zwischen 50 und 1000 V liegen.
mit ,
dem Durchbruchskniestrom, und
,
dem Durchbruch-Emissionskoeffizient.
Für die meisten Halbleiterdioden ist dieser Zustand unerwünscht, da er bei gewöhnlichen Dioden aufgrund der hohen Verlustleistung und des dünnen, eingeschnürten Stromflusskanals das Bauelement zerstört. Ursache für den Durchbruch sind sehr hohe elektrische Feldstärken. Es lassen sich drei unterschiedliche Mechanismen unterscheiden: der Lawinen-, der Zener- und der thermische Durchbruch.
Der Lawinendurchbruch (auch Avalanchedurchbruch oder Avalancheeffekt genannt) zeichnet sich durch eine Ladungsträgervervielfachung durch Stoßionisation aus. Er wird beispielsweise bei der IMPATT- und Suppressordiode, der Avalanche-Photodiode, sowie bei Z-Dioden (auch Zener-Dioden genannt) höherer Spannung genutzt (siehe auch unter Avalanche-Diode). Der Lawinendurchbruch ist auch bei manchen Gleichrichterdioden-Typen (Lawinengleichrichterdiode, Avalanche Type) zulässig und spezifiziert, so dass diese bei einmaligen oder periodischen Überspannungsereignissen bis zu bestimmten Energien nicht zerstört werden.
Bei Netzdioden, z. B. 1N4007 ist das Überschreiten der maximal zulässigen Sperrspannung – auch kurzfristig für wenige Mikrosekunden – nicht zulässig. Der dann fließende Lawinenstrom führt unmittelbar zur Zerstörung der Sperrschicht. Für den Betrieb von Diodengleichrichtern am Netz sind Überspannungsableiter, z. B. Varistoren erforderlich, die die Netz-Überspannung auf ein für die Gleichrichterdioden zulässiges Maß begrenzen.
Beim Zener-Durchbruch
werden hingegen durch eine spezielle Dotierung die Energiebänder stark
verschoben. Beim Überschreiten der Durchbruchspannung – in diesem Fall spricht
man meist von der Zenerspannung
– tritt ein Tunneleffekt
auf, der es Valenzbandelektronen ermöglicht, ohne Energieaufnahme vom Valenzband
in das Leitungsband zu wechseln. Der Zener-Durchbruch wird bei Z-Dioden bis etwa
5 Volt verwendet und dient unter anderem der Bereitstellung von
Referenzspannungen.
Der thermische Durchbruch beschreibt den Zusammenbruch der Sperrspannung aufgrund hoher Temperatur und der damit verbundenen Ladungsträgergeneration. In der Regel führt er zur Zerstörung der Diode durch Diffusionsvorgänge.
Differentieller Widerstand
Der differentielle Widerstand ergibt sich aus der Tangente durch den Arbeitspunkt der Diode. Er wird auch als dynamischer Widerstand bezeichnet. Durch die Verwendung einer Geraden anstatt der tatsächlichen Exponentialfunktion werden die benötigten Rechenschritte wesentlich vereinfacht.
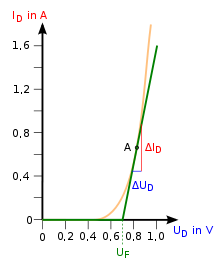
Arbeitspunkt: A
Bei großen Strömen wird
sehr klein, und der Bahnwiderstand
tritt zunehmend in Erscheinung. Dies ist ein realer Widerstand und rührt
wesentlich aus der Leitfähigkeit des Grundmaterials des Diodenchips. Er ist im
Ersatzschaltbild mit
in Serie.
Die Ersatzschaltung mit
und
eignet sich je nach Diodentyp nur bis zu Frequenzen von 10 bis 100 kHz. Bei
höheren Frequenzen, wie sie auch beim Ein- und Ausschalten auftreten, muss man
zusätzlich die kapazitiven Eigenschaften sowie die Sperrerholzeit der Diode
berücksichtigen.
Bahnwiderstand
Der Bahnwiderstand
wird durch den elektrischen Widerstand des Halbleitermaterials sowie dem
Widerstand des Anschlusses am Halbleiter verursacht. Der Bahnwiderstand wird
durch die folgende Formel berücksichtigt:
Statisches Kleinsignalmodell
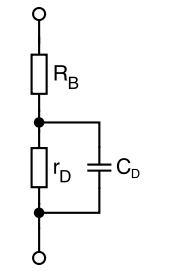
Das statische
Kleinsignalmodell wird zur Dimensionierung der Arbeitspunkteinstellung von
einfachen Schaltungen herangezogen. Hier entspricht
dem bereits genannten differentiellen
Widerstand (s.o.). Hinzu kommt gegebenenfalls noch der Bahnwiderstand.
Für den Betrieb um den Rückwärtsdurchbruch, also als Z-Diode, dient der
Parameter
zur Modellierung des Verhaltens.
Dynamisches Kleinsignalmodell
Für Wechselstromanwendungen muss man auch die Kapazitäten der Diode berücksichtigen, welche vor allem bei hohen Frequenzen hervortreten. Hierbei unterscheidet man zwischen der Sperrschichtkapazität und der für Schaltanwendungen bedeutenden Diffusionskapazität.
Das dynamische Kleinsignalmodell berücksichtigt zusätzlich zum statischen Kleinsignalmodell auch die Kapazität der Diode. Damit kann man auch einfache (Niederfrequenz-)Schaltungen mit Kapazitätsdioden dimensionieren.
Sperrschichtkapazität
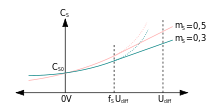
Der p-n-Übergang einer Diode hat eine Kapazität, die von der Breite der Raumladungszone abhängig ist. Mit steigender Sperrspannung vergrößert sich die Breite der ladungsfreien Zone, wodurch die Kapazität abnimmt.
Die Null-Kapazität
ist direkt proportional zur Fläche des pn-Überganges. Die
Diffusionsspannung
ist ebenfalls von der Dotierung abhängig. Mit steigender Dotierung nehmen
und
zu. Die Diffusionsspannung
liegt üblicherweise im Bereich zwischen 0,5 und 1 Volt.
Der Kapazitätskoeffizient
stellt das Dotierungsprofil des pn-Überganges dar. Direkte Übergänge von der p-
in die n-Schichten führen zu einem Wert von
,
während Übergänge mit linearem Verlauf von der p- in die n-Schichten zu einem
Wert von
führen.
Die obenstehende Formel für
ist nur bis zu einem Wert von etwa
gültig. Die Formel kann also – wie in der Grafik punktiert dargestellt – den
tatsächlichen Verlauf von
in diesem Bereich nicht wiedergeben. Über diesem Wert nimmt
nur noch schwach zu. Für einen Wert von
wird der weitere Verlauf von
durch die Tangente im Punkt
ersetzt, welches dem tatsächlichen Verlauf sehr nahekommt:
Durch Einsetzen erhält man die Gleichung
Hierbei ist .
Diffusionskapazität
Bei Anlegen einer Durchlassspannung kommt es in den Bahngebieten (also außerhalb der Raumladungszone) zu Minoritätsträgerüberschüssen, die die so genannten Diffusionsladungen bilden. Diese räumlich getrennten Ladungen müssen bei Änderungen der Durchlassspannung auf- bzw. abgebaut werden und beeinflussen somit das dynamische Verhalten der Diode.
IDD wird als Diffusionsstrom bezeichnet, und
ist die so genannte Transitzeit:
Näherungsweise kann man auch annehmen, dass für den Diffusionsbereich
und damit auch
gilt. Daraus ergibt sich die Näherungsgleichung:
- Bei Si-Dioden
ist
.
- Bei Schottky-Dioden
ist
, deshalb kann bei Schottky-Dioden die Diffusionskapazität meist vernachlässigt werden.
Die Diffusionskapazität bzw. die Sperrerholzeit verursacht Verluste bei schnellen Schaltanwendungen (Schaltnetzteile); daher verwendet man hier – falls Schottkydioden aufgrund ihrer begrenzten Sperrspannung nicht angewendet werden können – besonders schnelle Siliziumdioden. Für Dioden in HF-Schalter wie der pin-Diode ist dagegen eine große Diffusionskapazität gewünscht, um eine niedrige Impedanz bei hohen Frequenzen zu erreichen.
Schaltverhalten
Das Schaltverhalten kann nur sehr eingeschränkt mit dem Kleinsignalmodell beschrieben werden, denn hier ist das nichtlineare Verhalten der Diode wichtig. Die Beschreibung durch die Diffusionskapazität gibt für das „Ausschalten“ zwar ein qualitativ passendes Bild, liegt aber wegen der Nichtlinearität quantitativ daneben.
Der Wechsel von der Stromleitung in Durchlassrichtung zum Sperrverhalten geht
bei einer PN-Diode nicht sofort. Zuerst müssen die zusätzlichen
Minoritätsladungsträger entfernt werden. Wenn nicht auf die Rekombination
gewartet wird, fließen die Minoritätsladungsträger als
Reverse-Recovery-Ladung ()
als kurzer Strompuls in Sperrrichtung ab. Erst danach wird die Spannung negativ
und die Diode geht mehr oder weniger abrupt in den sperrenden Zustand über. Die
Zeit, bis die Diode sperren kann, wird Sperrerholzeit (
)
genannt und ist von der Größenordnung der Transitzeit.
Diese Verzögerungszeit erlaubt es, langsame pin-Dioden als gleichstromgesteuerte Wechselspannungswiderstände für elektronische Schalter und regelbare Dämpfungsglieder für Hochfrequenzsignale (Periodendauer kurz gegen die Sperrerholzeit) zu verwenden. Umschaltbare Phasenschieber mit pin-Dioden werden auch in Phased-Array-Antennen benötigt.
Oft ist ein schneller Übergang in den sperrenden Zustand gefragt und es werden entsprechend schnelle Dioden mit kurzer Transitzeit (Größenordnung 5–200 ns für Silizium-PN-Dioden) angeboten. Bei Schottkydioden spielen die Minoritätsladungsträger keine wesentliche Rolle und entsprechend gibt es einen sehr schnellen Übergang in den sperrenden Zustand.
Auch der Übergang vom sperrenden Zustand in den leitenden Zustand geschieht nicht sofort, wenn auch recht schnell. Besonders bei PIN-Dioden für hohe Sperrspannungen braucht es eine gewisse Zeit, bis die Minoritätsladungsträger die Sperrschicht bzw. den intrinsischen Bereich geflutet haben. Bei einem sehr schnellen Anstieg des Stromes kann die Spannung in Flussrichtung anfangs deutlich höher werden als im stationären Fall. Die üblichen Bezeichnungen sind tfr für das Wieder-Erreichen von 110 % der nominalen Flussspannung und Vfp für den maximalen Wert des Überschwingens (overshoot) der Flussspannung. Bei „normalen“ Dioden (keine PIN) ist die Verzögerung recht kurz, bzw. das Überschwingen der Spannung gering und eher selten relevant.
Der Ab- und Zufluss der Minoritätsladungsträger repräsentiert die Schaltverluste der Diode, die bei höherfrequenten Leistungsanwendungen (Schaltnetzteile) die Leitverluste übersteigen können.
Kennzeichnung und Beschriftung

Die Kathode unipolarer Dioden ist meist mit einem Ring oder Farbpunkt gekennzeichnet. Der Kathodenanschluss von Leuchtdioden ist durch einen Farbpunkt, ein kürzeres Anschlussbein und/oder eine Gehäuseabflachung gekennzeichnet. Bei Laserdioden ist die Anode meist mit dem Gehäuse verbunden.
Der Diodentyp kann nach zwei Standards gekennzeichnet sein: Gemäß JEDEC-Norm oder gemäß Pro-Electron, jeweils mit einem Farbcode oder einer Beschriftung. Bei der Bezeichnung mit Farbcode ist der erste Ring breiter aufgedruckt und bezeichnet gleichzeitig den Anschluss der Kathode. Bei der Beschriftung wird die Kathode mit einem Ring gekennzeichnet. Einige Hersteller führen eigene Benennungsschemen.
Auch erwähnenswert ist die Kennzeichnung auf Brückengleichrichtern mit je zwei Anschlüssen für die anzulegende Wechselspannung „AC“ und die entnehmbare Gleichspannung „+“ und „−“. In der Typenbezeichnung sind oft die maximal zulässige Sperrspannung und Nennstrom enthalten, wobei etwa „E40 C30“ für 40 V Spannung (E) und 30 mA Strom (C) steht.
JEDEC
Die Beschriftung für Dioden gemäß JEDEC Solid State Technology Association (USA) setzt sich aus einer Zahl und einem Buchstaben sowie einer weiteren vierstelligen Zahl zusammen (z.B. „1N4148“). Die vierstellige Zahl kann hierbei in der folgenden Farbcodierung angegeben sein:
| Farbe | schwarz | braun | rot | orange | gelb | grün | blau | violett | grau | weiß |
|---|---|---|---|---|---|---|---|---|---|---|
| Wert | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Pro-Electron
Die Beschriftung der Dioden nach Pro-Electron (EECA (European Electronic Component Manufacturers Association)) setzt sich aus zwei bis drei Buchstaben und einer zwei- bis dreistelligen Zahl zusammen.
Beispiele: B A 159, B A T 20
- Kennbuchstabe = Ausgangsmaterial
- Kennbuchstabe = Hauptfunktion
- Kennbuchstabe = Hinweis auf kommerziellen Einsatz (als dritter Buchstabe wird bei kommerziellen Bauelementen X, Y oder Z benutzt)
- Ziffern = Registernummer (2 oder 3 Ziffern)
Die Buchstaben-Ziffernfolge kann alternativ als Farbcode angegeben werden:
| Farbe | 1. Ring | 2. Ring | 3. Ring | 4. Ring |
|---|---|---|---|---|
| schwarz | X | 0 | 0 | |
| braun | AA | 1 | 1 | |
| rot | BA | 2 | 2 | |
| orange | S | 3 | 3 | |
| gelb | T | 4 | 4 | |
| grün | V | 5 | 5 | |
| blau | W | 6 | 6 | |
| violett | 7 | 7 | ||
| grau | Y | 8 | 8 | |
| weiß | Z | 9 | 9 |
Kenngrößen
Halbleiterdioden (Signaldioden, Gleichrichterdioden, aber auch Laser-, Schutz- und Leuchtdioden) haben bestimmte Kenngrößen zur Spezifikation. Sie sind in den Datenblättern genannt und sind wichtig für die Anwendung und die Bemessung deren Beschaltung mit anderen Bauteilen.
Die wichtigsten Kenngrößen und Grenzwerte von Dioden sind:
- maximal zulässige Sperrspannung (Gleichrichter- und Signaldioden, Leucht- und Laserdioden)
- maximaler Dauer- und Spitzenstrom in Durchlassrichtung (Gleichrichter- und Signaldioden, Leucht- und Laserdioden)
- die Flussspannung oder auch Schleusenspannung
bei einem bestimmten Strom (⅟10 Nennstrom für Gleichrichterdioden)
- bei Zenerdioden die maximale Dauer-Verlustleistung und die Zenerspannung
- bei Gleichrichter- und Signaldioden die Schaltzeit (auch Sperrverzögerungszeit oder Sperr-Erholzeit, engl. reverse recovery time, kurz trr genannt)
- bei Suppressordioden (TVS) die Ansprechzeit, die Energie und die Spitzenleistung, die beim Avalanche-Durchbruch in Sperrrichtung absorbiert werden kann, die Durchbruchspannung sowie die maximal ohne Durchbruch garantierte Spannung in Sperrrichtung
- insbesondere bei Schottkydioden der stark temperaturabhängige Leckstrom (Sperrstrom)
Diodentypen und Anwendung

Es gibt eine Reihe von Dioden für unterschiedliche Einsatzzwecke:
- Gleichrichtung
- Die Umwandlung von Wechselspannung in Gleichspannung erfolgt bei niedrigen Frequenzen fast ausschließlich durch Silizium-PN-Dioden. Bei sehr großen Leistungen (Leistungsgleichrichter) verwendet man p+sn+-Dioden. Veraltete Typen sind die Germaniumdiode, der Kupferoxydul-Gleichrichter, der Selen-Gleichrichter („Trockengleichrichter“) und die Röhrendiode. Verpolungsschutz-Dioden und Freilaufdioden sind ebenfalls Gleichrichterdioden. Hochspannungsdioden bestehen aus mehreren in einem Gehäuse in Reihe geschalteten Diodenchips. Bei besonders hohen Frequenzen werden bis etwa 200 V Sperrspannung Silicium-Schottky-Dioden eingesetzt. Bei hohen Sperrspannungen (aktuell bis etwa 1600 V), hohen Frequenzen und Einsatztemperaturen werden immer öfter Siliciumcarbid-Schottky-Dioden eingesetzt. Diese haben wie auch Silicium-Schottky-Dioden keine Schaltverluste.
- Kleinsignaldioden
- Kleinsignal-Dioden dienen der Gleichrichtung von kleinen Strömen und Signalen (Demodulator hierfür wurden früher auch Röhrendioden verwendet), als Mischer, als Spannungsreferenz, zur Temperaturmessung bzw. -kompensation bei Siliziumdioden ca. 0,7 V, temperaturabhängig) und als Schaltdiode für einfache Logikverknüpfungen.
- Spannungsstabilisierung
- Für die Spannungsstabilisierung und zur Überspannungsbegrenzung kommen Zener-Dioden (auch Z-Diode genannt) und die ähnlich aufgebauten Suppressordioden zum Einsatz. Hier wird der in Sperrrichtung auftretende Zenereffekt und der Avalancheeffekt genutzt. Bipolare Suppressordioden für den Einsatz an Wechselspannung bestehen aus zwei gegeneinander in Serie geschalteten unipolaren Dioden.
- Optik
- Für optische Zwecke dienen die Laserdiode, die Photodiode, die Avalanche-Photodiode und die Leuchtdiode (kurz LED).
Wortherkunft
Das Wort Diode stammt von altgriechisch δίοδος> díodos „Durchgang“, „Pass“, „Weg“; das Substantiv setzt sich zusammen aus der Präposition διά diá „durch“, „hindurch“ sowie dem Wort ὁδός hodós „Weg“.
Literatur
- Ulrich Tietze, Christoph Schenk, Eberhard Gamm: Halbleiter-Schaltungstechnik. 12. Auflage. Springer, Berlin 2002, ISBN 3-540-42849-6.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 16.06. 2024