Seiliger-Kreisprozess

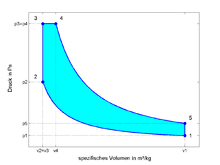
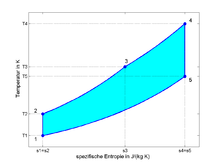
Druck-Volumen-Diagramm des Seiliger-Prozesses

Temperatur-Entropie-Diagramm des Seiliger-Prozesses

Der Seiliger-Kreisprozess ist ein gemischter Vergleichsprozess (Gleichraum- und Gleichdruckprozess), der verwendet wird, um die Vorgänge in Verbrennungsmotoren darzustellen. Er bildet den sogenannten vollkommenen Motor ab. Sowohl der Gleichdruckprozess als auch der Gleichraumprozess sind als Spezialfälle im Seiliger-Prozess enthalten.

Der Gleichdruckprozess (Diesel-Prozess) mit seiner rein isobaren Wärmezufuhr kann in der Praxis nicht realisiert werden, da eine Wärmezufuhr ohne Druckerhöhung nicht möglich ist. Der Gleichraumprozess (Otto-Prozess) mit seiner rein isochoren Wärmezufuhr kann in der Praxis nicht realisiert werden, da eine beliebig schnelle Wärmezuführung nicht möglich ist. Die teilweise isobare und teilweise isochore Wärmezufuhr im Seiliger-Prozess liefert eine gute Annäherung an die real ablaufenden Prozesse in Diesel- und Ottomotoren.

Prozessablauf

Der 1922 von Myron Seiliger vorgeschlagene Vergleichsprozess gliedert sich bei Motoren ohne Motoraufladung in fünf Prozessschritte:

(1 - 2) isentrope Verdichtung. Energieübertragung in Form von Arbeitsaufwand $w>0$ .
(2 - 3) isochore Verbrennung. Energieübertragung in Form von Heizwärme .
(3 - 4) isobare Verbrennung. Energieübertragung durch Heizwärme und Nutzarbeit durch Ausdehnung. $q>0,w<0$ .
(4 - 5) isentrope Entspannung. Energieübertragung in Form von Nutzarbeit $w<0$ .
(5 - 1) isochores Auspuffen. Energieübertragung in Form von Abwärme und Arbeitsaufwand $q<0,w>0$ .

Dabei bedeuten positive Wärme- oder Arbeitsenergiewerte eine Energiezufuhr und negative Arbeits- oder Wärmeenergiewerte eine Energieabgabe an das Arbeitsgas. Der Gaswechselzyklus (isobares Ausstoßen und Ansaugen) ist nicht berücksichtigt.

Wirkungsgrad

Der thermische Wirkungsgrad des Seiliger-Prozesses hängt neben dem Volumenverhältnis $\varepsilon$ (Expansionsverhältnis, Verdichtungsverhältnis) und dem Isentropenexponent $\kappa$ von der Aufteilung der zugeführten Wärmemenge für das Drucksteigerungsverhältnis $\xi$ und der Wärmemenge für das Voll- oder Gleichdruckverhältnis $\psi$ ab und lässt sich folgendermaßen bestimmen:

$\eta _{th\,\mathrm {Seiliger} }=1-{\frac {1}{\varepsilon ^{\kappa -1}}}\cdot {\frac {\psi ^{\kappa }\xi -1}{\xi -1+\kappa \xi (\psi -1)}}$

Der erste Hauptfaktor ist der thermodynamische Verlust für den Gleichraumprozess. Der zweite Hauptfaktor ist der zusätzliche Verlust durch den Gleichdruckprozess und somit größer als 1. Der Gleichraumprozess ist effizienter als der Gleichdruckprozess. Der thermische Wirkungsgrad des Seiliger-Prozesses liegt zwischen dem Gleichraumprozess und dem Gleichdruckprozess.

$\varepsilon ={\frac {V_{1}}{V_{2}}}$ ; V₁ ist das Expansionsvolumen bzw. der Ausdehnungsraum. V₂ das Kompressionsvolumen bzw. der Verdichtungsraum.

$\kappa = \frac{c_p}{c_V}$ ; Isentropenexponent (Brenngas bzw. Abgas von 1000 °C hat einen Wert von ca. 1,3). Je höher das Verhältnis von c_p zu c_V desto höher der Wirkungsgrad.

$c_{p}$ ; Spezifische Wärmekapazität bei konstantem Druck (Brenn- bzw. Abgas von 1000 °C hat ca. 1,25 kJ/(kg K).

$c_{V}$ ; Spezifische Wärmekapazität bei konstantem Volumen (Brenn- bzw. Abgas von 1000 °C hat ca. 0,96 kJ/(kg K).

$R_{s}=c_{p}-c_{V}$ ; Spezifische Gaskonstante. Sie bleibt über einen großen Temperaturbereich konstant und beträgt für Frischgas und Abgas ca. 0,29 kJ/(kg K).

$\xi ={\frac {p_{3}}{p_{2}}}={\frac {T_{3}}{T_{2}}}$ ; Druck- und Temperatursteigerungsverhältnis mit isochorer Verbrennung. Je größer die Druck- und Temperatursteigerung, desto höher der thermische Wirkungsgrad.

$p_{2}=p_{1}\cdot \varepsilon ^{\kappa }$ ; Verdichtungsdruck. p₁ ist der Anfangsdruck, z.B. 1 bar.

$T_{2}=T_{1}\cdot \varepsilon ^{\kappa -1}$ ; Verdichtungstemperatur. T₁ ist die Anfangstemperatur in Kelvin (Frischgas und Restabgas) vor dem Verdichtungstakt, z.B. 400 K (ca. 127 °C).

$p_{3}=p_{2}{\frac {T_{3}}{T_{2}}}$ und $T_{3}=T_{2}{\frac {p_{3}}{p_{2}}}$ ; Druck und Temperatur nach der Gleichraumverbrennung. p₃ und T₃ ergeben sich aus der gewählten Heizenergiemenge für die isochore Temperatur- und Drucksteigerung.

$\psi ={\frac {V_{4}}{V_{3}}}={\frac {T_{4}}{T_{3}}}$ ; Raum- und Temperatursteigerungsverhältnis (Ausdehnungs-, Volldruckverhältnis) bei isobarer Verbrennung. T₄ und V₄ ergeben sich aus der gewählten Aufteilung von Gleichraum- und Gleichdruckverhältnis. Je geringer die Gleichdruckzahl desto höher der Wirkungsgrad.

$\eta _{th\,\mathrm {Carnot} }=1-{\frac {T_{1}}{T_{4}}}$ ; Der Carnot-Wirkungsgrad bestimmt die theoretische Obergrenze aller thermodynamischen Kreisprozesse.

Zur Veranschaulichung der Zustandsgrößen wird im Folgenden ein ideales Gas mit temperaturunabhängiger und gleicher Wärmekapazität für Verdichtung und Expansion benutzt.

Aufteilung Drucksteigerung – Raumsteigerung

Die Wärmezufuhr des gemischten Prozesses setzt sich wie folgt zusammen:

$Q_{zu}=Q_{V}+Q_{P}=m\left[c_{V}({\frac {T_{3}}{T_{2}}}-1)T_{2}+c_{p}({\frac {T_{4}}{T_{3}}}-1)T_{3}\right]$ Wärmezufuhr (kJ) für den gesamten Arbeitstakt. Q_V ist der Wärmeumsatz bei konstantem Volumen und Q_P ist der Wärmeumsatz bei konstantem Druck. Beim Dieselmotor mit mehrfacher Direkteinspritzung kann die Aufteilung frei gewählt werden. Beim Benzinmotor ohne Direkteinspritzung kann die Aufteilung nur über den Zündzeitpunkt beeinflusst werden. m ist die Heiz- oder Gemischmasse des Arbeitsgases (kg).

Statt mit absoluten Heizenergien und Massen zu rechnen, wird im Folgenden mit spezifischen Heizenergien und Massen gerechnet.

$\!H_{u}=H_{V}+H_{P}$ ; spezifische Heizenergie (kJ/kg) für den gesamten Arbeitstakt. H_V ist der Heizenergieanteil für die Gleichraumphase und H_P für die Gleich- oder Volldruckphase. Zum Beispiel: 42'000 kJ/kg H_u = 20'000 kJ/kg H_V + 22'000 kJ/kg H_P. Je mehr Energie für die Gleichraumphase, desto höher der Wirkungsgrad.

$T_{3}=T_{2}+{\frac {H_{V}}{m_{H}c_{V}}}$ ; Temperatur nach der Gleichraumverbrennung. m_H ist die spezifische Heizmasse zu Brennstoffmasse (kg/kg). Für ein Luftverhältnis von $\lambda$ =1 braucht es 18 kg Luft und Restabgas pro kg Benzin, also etwa 20 % mehr als das Minimum für Luft. c_V = c_p / κ.

$T_{4}=T_{3}+{\frac {H_{P}}{m_{H}c_{p}}}$ ; Höchsttemperatur nach der Gleichdruckverbrennung. m_H ist die spezifische Heizmasse pro Brennstoffmasse (kg/kg). Für ein Luftverhältnis von $\lambda$ =1,4 braucht es 25 kg Luft und Luftüberschuss und Restabgas pro kg Diesel. c_p = c_V · κ. Die spezifische Wärmekapazität c_p der Heizmasse (Brenngas bzw. Abgas bei ca. 1000 °C) beträgt etwa 1.2 kJ/(kg K), für c_v etwa 0.9 kJ/(kg K).

Drucksteigerungsverhältnis

Die Drucksteigerung p₃/p₂ entspricht auch der Temperaturerhöhung T₃/T₂ während der Gleichraumphase. Die absolute Druckzunahme p₃-p₂ ist direkt abhängig von der gewählten spezifischen Energiezufuhr H_V.

$\xi ={\frac {H_{V}}{m_{H}c_{V}T_{2}}}+1$ ; Drucksteigerungszahl. H_V ist die Heizenergie (kJ/kg) für die Gleichraumphase. Je höher die Drucksteigerung desto höher der Wirkungsgrad.

$p_{3}=p_{2}\cdot \xi$ und $T_{3}=T_{2}\cdot \xi$ ; Druck und Temperatur nach der Gleichraumverbrennung. p₃ ist der Maximaldruck.

Raumsteigerungsverhältnis

Die Volumenvergrößerung V₄/V₃ entspricht auch der Temperaturerhöhung T₄/T₃ während der Gleichdruckphase. Die absolute Temperaturzunahme T₄-T₃ ergibt sich direkt aus der verbliebenen (H_u - H_V) spezifischen Energiezufuhr H_P.

$\psi ={\frac {H_{P}}{m_{H}c_{p}T_{3}}}+1$ ; Temperatur- und Raumsteigerungszahl für den Gleichdruckprozess. T₁ ist die Anfangstemperatur nach dem Ansaugtakt vor der Verdichtung und H_u die zugeführte spezifische Heizenergie (kJ/kg) für den gesamten Arbeitstakt. Wenn $\xi$ bekannt ist, kann auch folgende Formel angewandt werden:

$\psi ={\frac {H_{u}}{m_{H}c_{p}T_{1}\varepsilon ^{\kappa -1}\xi }}-{\frac {1}{\kappa }}+{\frac {1}{\kappa \xi }}+1$

$T_{4}=T_{3}\cdot \psi$ und $V_{4}=V_{3}\cdot \psi$ ; Temperatur und Volumen nach der Gleichdruckverbrennung. T₄ ist die Höchsttemperatur.

Dieselmotor

Im Dieselmotor werden diese fünf Prozessschritte wie folgt realisiert:

(1 - 2) Der Kolben bewegt sich in Richtung oberer Totpunkt. Die sich im Zylinder befindliche Luft wird verdichtet. Das heißt, es wird Arbeit an der Luft verrichtet.
(2 - 3) Der Dieselkraftstoff wird vor dem oberen Totpunkt in den Brennraum eingespritzt. Durch die hohe Temperatur der komprimierten Luft entzündet sich der Einspritzstrahl und die innere Energie des Brennstoffs wird in Form von Wärme freigesetzt. Dies erfolgt in diesem Prozessschritt zunächst bei ungefähr gleichbleibendem Volumen.
(3 - 4) Durch die andauernde Verbrennung über den oberen Totpunkt hinaus wird die Temperatur bei etwa gleichem Druck der Brenngase weiter erhöht.
(4 - 5) Die Verbrennung endet nun und das Verbrennungsgas entspannt sich bei gleichbleibender Entropie. Es wird technische Arbeit am Kolben geleistet (Kraft mal Weg). Das Volumen des Verbrennungsgases steigt an, Druck und Temperatur sinken, bis der Kolben den unteren Totpunkt erreicht.
(5 - 1) Das Auslassventil wird geöffnet, das heiße Abgas verlässt mit Überdruck den Brennraum. Restgas und Wärme wird mit wenig Gegendruck ausgestoßen.

Ottomotor

Im Ottomotor werden diese fünf Prozessschritte wie folgt realisiert:

(1 - 2) Der Kolben bewegt sich in Richtung oberer Totpunkt und das Luft-Kraftstoff-Gemisch wird verdichtet. Das heißt, es wird Arbeit am Luft-Kraftstoff-Gemisch verrichtet.
(2 - 3) Die Zündkerze startet die Verbrennung des Luft-Kraftstoff-Gemisches vor dem oberen Totpunkt und die innere Energie des Brennstoffs wird in Form von Wärme und Druck freigesetzt. Dies erfolgt zunächst bei ungefähr gleichem Volumen (isochor).
(3 - 4) Nach dem oberen Totpunkt des Kolbens erreicht die Verbrennung vor der Höchsttemperatur nun Höchstdruck, der solange gehalten wird (isobar), bis der Hauptteil des Gemisches verbrannt ist und die Temperatur wieder sinkt.
(4 - 5) Das Gemisch verbrennt nun vollständig und das Brenngas entspannt sich weiter bei gleichbleibender Entropie, bis der Kolben den unteren Totpunkt erreicht. In dieser Prozessphase wird am Kolben technische Arbeit geleistet (Arbeitstakt).
(5 - 1) Das Auslassventil wird geöffnet und das Abgas entweicht zuerst durch den Restdruck und dann durch die Aufwärtsbewegung des Kolbens. Dabei wird Energie in Form von Restdruck und Wärme abgeführt.

Realer Prozess beim Viertakter

Logarithmisches pV-Diagramm für Viertaktmotoren (inklusiv Ladungswechsel)

Das Ansaugen und Ausschieben ist mit Reibungs- und Pumpverlusten verbunden (linksdrehende Schleife im pV-Diagramm für die Ladungswechselarbeit). Die Voreinspritzung und die Vorzündung erfolgen weit vor dem oberen Totpunkt, was ebenfalls negativ in die Nutzarbeitsbilanz einfließt. Ein Teil der Verbrennungsenergie (neben endothermer Bildung von Stickoxid und andern schädlichen Abgasen) geht ohne Arbeitsleistung durch Wärmeübergang an die Brennraumwände verloren. Der Höchstdruck ist tiefer als der rechnerische wegen Abdichtungsverlusten. Die Expansionskurve liegt somit unterhalb des idealen Verlaufes. Das Auslassventil wird vor dem unteren Totpunkt geöffnet, was die Prozessfläche (Arbeitsleistung) abrundet und verkleinert.

Siehe auch

Carnot-Prozess (theoretisch maximaler thermodynamischer Wirkungsgrad)

Literatur

Wolfgang Kalide: Kolben und Strömungsmaschinen. 1. Auflage. Carl Hanser Verlag, München / Wien 1974, ISBN 3-446-11752-0.
Heinz Herwig: Technische Thermodynamik. 1. Auflage. Pearson Studium, München 2007, ISBN 978-3-8273-7234-5.

Basierend auf einem Artikel in:

Wikipedia.de