
Reguläre Fläche
Eine reguläre Fläche oder differenzierbare Fläche oder kurz Fläche ist ein mathematisches Objekt aus der Differentialgeometrie. Mit Hilfe dieses Begriffs wird der allgemein gebräuchliche Begriff der Fläche im mathematischen Kontext präzise definiert. Die folgende Definition bedeutet anschaulich, dass man Stücke einer Ebene verformt und diese derart zusammenheftet, dass keine Ecken oder Kanten entstehen, so dass man an jeder Stelle des entstandenen Gebildes eine Tangentialebene anlegen kann. Im Unterschied zur topologischen Fläche kann man auf der regulären Fläche – aufgrund der Existenz einer Tangentialebene – eine Ableitung einer Abbildung erklären.
Definition
Es gibt unterschiedliche, aber äquivalente Methoden, eine reguläre Fläche zu definieren. In der elementaren Differentialgeometrie wird eine reguläre Fläche durch eine Parametrisierung definiert. In der Differentialtopologie, einem abstrakteren Teilgebiet der Differentialgeometrie, sind die regulären Flächen zweidimensionale Spezialfälle n-dimensionaler differenzierbarer Mannigfaltigkeiten.
Durch Parametrisierungen
Eine Teilmenge
heißt reguläre Fläche, falls für jedes
eine Umgebung
,
eine offene Menge
und eine Abbildung
existieren, so dass
- die Abbildung
ein Homöomorphismus ist. Sie ist also stetig, bijektiv und hat eine stetige Umkehrfunktion.
- die Abbildung
stetig differenzierbar ist.
- für jeden Punkt
das Differential
vollen Rang hat, also injektiv ist.
Die Abbildung
heißt Parametrisierung.
Durch die dritte Forderung ist sichergestellt, dass man an jeden Punkt der
Fläche eine Tangentialebene
anheften kann.
Als zweidimensionale Mannigfaltigkeit
Alternativ kann eine reguläre Fläche auch als topologische Fläche mit einer differenzierbaren Struktur verstanden werden. Insbesondere ist eine reguläre Fläche eine zwei-dimensionale, differenzierbare Untermannigfaltigkeit.
Beispiele
Reguläre Flächen
Beispiele für reguläre Flächen sind die 2-Sphäre, der Ellipsoid, der Hyperboloid und der Torus. Der Torus und die 2-Sphäre (Kugeloberfläche) werden gleich näher diskutiert. Der Beweis, dass diese Objekte reguläre Flächen sind, lässt sich oftmals auch einfach mit dem Satz vom regulären Wert aus der Differentialgeometrie führen. Insbesondere ist jede zwei-dimensionale, differenzierbare Mannigfaltigkeit eine reguläre Fläche.
Konkrete Parametrisierungen
Parametrisierungen spielen eine wichtige Rolle im Bezug auf Oberflächenintegrale.
Lässt sich eine Fläche
durch eine differenzierbare Funktion mit
beschreiben, so erhält man mit
eine Parametrisierung und die Fläche ist regulär. Jedoch kann man auf diese
Weise nur Flächen parametrisieren, bei welchen man keinem Paar
mehr als einen z-Wert zuordnen muss. Die zwei folgenden und oft verwendeten
Beispiele lassen sich also, wenn man nur eine Parametrisierungsabbildung
verwenden will, so nicht darstellen.
Kugel
Durch die Abbildung ,
welche durch
gegeben ist, erhält man eine Kurvenparametrisierung der Kreislinie eines Halbkreises
in der rechten Halbebene mit Radius
und Mittelpunkt Null, wie die Gleichung
zeigt.
Mit Hilfe dieser Kurvenparametrisierung erhält man die Parametrisierung einer
Kugeloberfläche,
welche durch die Funktion
mit
beschrieben wird. Dass die aus der Definition geforderten Eigenschaften für
gelten, ist unter Kugelkoordinaten
nachzulesen. Jedoch muss man beachten, dass diese Parametrisierung die Punkte
und
"vergisst". Es ist nicht möglich, eine komplette Kugel mit einer globalen
Parametrisierung zu beschreiben. Dafür werden mindestens zwei Abbildungen
benötigt.
Anschaulich erhält man diese Parametrisierung, indem man an einem beliebigen
Punkt auf der Kugel startet und sie auf einem Halbkreis umläuft und bei jedem
Punkt, den man erreicht, umläuft man die Kugel einmal komplett in der dazu
senkrechten Richtung. Außerdem kann man auch hier die Gleichheit
zeigen.
Torus
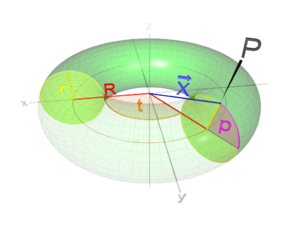
Sei .
Die Parametrisierung
der Kreislinie eines Kreises mit Radius
und Mittelpunkt
lautet ähnlich wie oben
Mit Hilfe dieser Kurvenparametrisierung erhält die Parametrisierung
eines Torus, welche durch
beschrieben werden kann. Anschaulich bedeutet dies, dass ein Torus entsteht, wenn man einen
Kreis mit Zentrum
nimmt und diesen um die
-Achse
um den Nullpunkt dreht.
Graphen differenzierbarer Funktionen
Wie in den Beispielen schon angesprochen ist der Graph einer differenzierbaren Funktion stets eine reguläre Fläche. Der Graph der Funktion
wird parametrisiert durch die Abbildung
Dass die Umkehrung nicht gilt, sieht man am Beispiel der Kugelschale. Jedoch
gibt es lokal eine Umkehrung der Aussage. Sei
eine reguläre Fläche und
ein Punkt. Dann existiert eine Umgebung
von p, so dass
der Graph einer differenzierbaren Funktion ist, welche die Form
hat.
Literatur
- Konrad Königsberger: Analysis. Band 2. 3. überarbeitete Auflage. Springer, Berlin u. a. 2000, ISBN 3-540-66902-7.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 29.08. 2022