Hyperwürfel

Projektion eines Tesseraktes (vierdimensionaler Hyperwürfel) in die 2. Dimension

Hyperwürfel oder Maßpolytope sind -dimensionale Analogien zum Quadrat ( n=2 ) und zum Würfel ( n=3 ). Dabei kann eine beliebige natürliche Zahl sein. Der vierdimensionale Hyperwürfel wird auch als Tesserakt bezeichnet. Die Symmetriegruppe eines Hyperwürfels ist die Hyperoktaedergruppe.

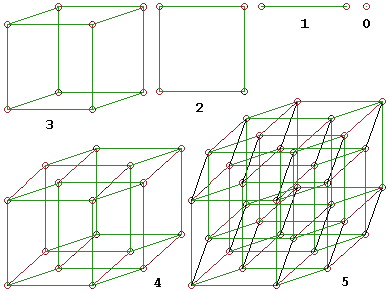
Konstruktion regulärer Würfel

Reguläre Würfel der Kantenlänge $a\neq 0$ lassen sich wie folgt erzeugen:

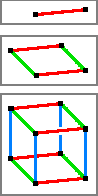
Wenn ein Punkt um die Distanz geradlinig verschoben wird, entsteht eine eindimensionale Strecke, mathematisch ein eindimensionaler Hyperwürfel.
Wenn diese Strecke senkrecht zu ihrer Dimension um die Distanz verschoben wird, entsteht ein zweidimensionales Quadrat, eine Fläche, mathematisch ein zweidimensionaler Hyperwürfel.
Wenn dieses Quadrat senkrecht zu seinen beiden Dimensionen um die Distanz verschoben wird, entsteht ein dreidimensionaler Würfel, mathematisch einem dreidimensionalen Hyperwürfel entsprechend.
Allgemein: Wenn also ein -dimensionaler Würfel senkrecht zu seinen Dimensionen um die Distanz verschoben wird, entsteht ein -dimensionaler Hyperwürfel.

Grenzelemente

In einem Hyperwürfel der Dimension befinden sich an jedem Knoten (Ecke) genau Kanten. Demnach handelt es sich bei einem Hyperwürfel um einen ungerichteten Multigraph (siehe auch: Graphentheorie).

Der -dimensionale Würfel wird von nulldimensionalen, eindimensionalen, …, $(n\!-\!1)$ -dimensionalen Elementen begrenzt. Am Beispiel:

Der 3-dimensionale Würfel wird von Knoten (Punkten), Kanten (Strecken) und Flächen begrenzt, also von Elementen der Dimension 0,1 und 2.

Die Anzahl der einzelnen Grenzelemente lässt sich aus folgender Überlegung ableiten: Sei ein Hyperwürfel von der Dimension $n\!+\!1$ gegeben. Die -dimensionalen Grenzelemente dieses Würfels ( $k_{{n+1}}$ ) lassen sich folgendermaßen aus den Grenzelementen eines -dimensionalen Hyperwürfels erzeugen: Die -dimensionalen Grenzelemente ( $k_{{n}}$ ) verdoppeln sich und alle $k\!-\!1$ dimensionalen Elemente $(k\!-\!1)_{n}$ werden zu -dimensionalen erweitert. Somit ergibt sich in der Summe eine Anzahl von $k_{{n+1}}=2k_{{n}}+(k-1)_{{n}}$ .

Beispiel

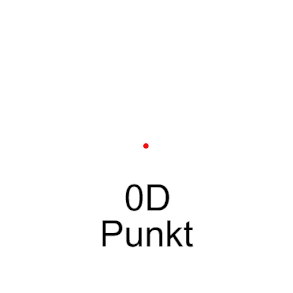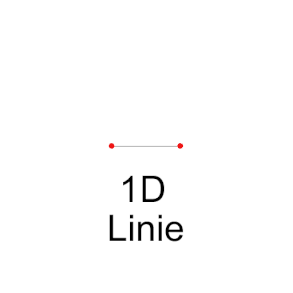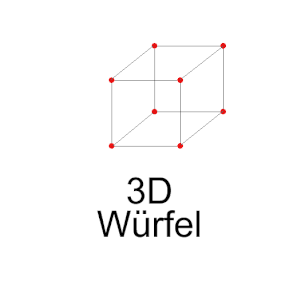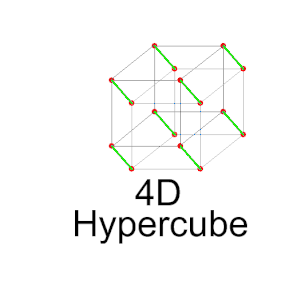
Der 2-dimensionale Hyperwürfel wird von 1 Fläche $(k_{{n}}=2)$ , 4 Kanten $(k_{{n}}=1)$ und 4 Knoten $(k_{{n}}=0)$ begrenzt.

Der 3-dimensionale Würfel wird von Flächen $(k_{{n+1}}=2)$ begrenzt, von Kanten $(k_{{n+1}}=1)$ und Knoten $(k_{{n+1}}=0)$ .

Anders kann man sich überlegen: Wenn man einen -dimensionalen Hyperwürfel in ein kartesisches Koordinatensystem um den Ursprung zentriert und nach den Koordinatenachsen ausgerichtet legt, gibt es zu einem -dimensionalen Grenzelement Koordinatenachsen, die parallel zu diesem Grenzelement sind. Andererseits gibt es aber zu jeder Auswahl von Koordinatenachsen nicht nur ein -dimensionales Grenzelement, sondern $2^{n-k},$ weil man durch jede der n-k zu den Grenzelementen senkrechten Achsen die Anzahl der Grenzelemente verdoppelt (es gibt dieselben Grenzelemente noch einmal parallelverschoben auf der anderen Seite der Achse). Die Anzahl der Grenzelemente ergibt sich also aus dem Produkt der Anzahl der Möglichkeiten, Achsen aus den Achsen auszuwählen, mit der Anzahl von Grenzelementen für jede Auswahl und lautet somit ${\binom {n}{k}}\cdot 2^{n-k}$ (mit dem Binomialkoeffizienten ${\binom {n}{k}}$ ).

Der Weg zum Hyperwürfel

Die 0- bis 5-dimensionalen Würfel in der Parallelprojektion

	Schläfli- Symbol	0-dim.	1-dim.	2-dim.	3-dim.	4-dim.	$\ldots$	$(n\!-\!1)$ -dim.	-dim.
	Schläfli- Symbol	Anzahl der Grenzelemente
Punkt		1
Strecke	$\{\}$	2	1
Quadrat	$\{4\}$	4	4	1
3-dim. Würfel	$\{4,3\}$	8	12	6	1
4-dim. Würfel	$\{4,3,3\}$	16	32	24	8	1
$\vdots$
-dim. Würfel	$\{4,3^{n-2}\}$	$2^{n}$	$n2^{{n-1}}$	${\binom {n}{2}}2^{n-2}$	${\binom {n}{3}}2^{n-3}$	$\ldots$	$\ldots$	${\binom {n}{n-1}}2^{1}=2n$	${\binom {n}{n}}2^{0}=1$

Jedes -dimensionale Grenzelement eines -dimensionalen Würfels der Kantenlänge ist für $0<k\leq n$ ein -dimensionaler Würfel derselben Kantenlänge . Damit hat ein 4-Hyperwürfel 16 Ecken, ein Kantennetz der Länge $32a$ , ist begrenzt von einem Flächennetz der Gesamtfläche $24a^{2}$ und von Zellen mit dem 3-Gesamtvolumen (der 3-dimensionalen Hyperfläche) von $8a^{3}$ und hat ein 4-Volumen von $a^{4}$ .

Eigenschaften

Die Konstruktion der längsten Diagonalen von Quadrat, Würfel und Tesserakt

Der Name Maßpolytop kommt von der Möglichkeit, das Objekt parallel zu allen Koordinatenachsen auszurichten und den euklidischen Raum durch parallele Vervielfältigung restlos auszufüllen. Es ist das einzige regelmäßige Polytop, mit dem dies in Dimensionen n>4 gelingt. Für jede Dimension sind diese Parkettierungen selbstdual mit dem Schläfli-Symbol $\{4,3^{n-2},4\}.$

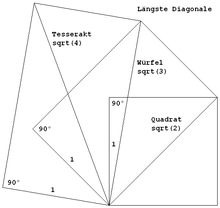
Die längste Diagonale eines Hyperwürfels entspricht der Quadratwurzel seiner Dimension multipliziert mit seiner Kantenlänge.

Maßpolytop (oder Hyperwürfel) und Kreuzpolytop (oder Hyperoktaeder) sind zueinander dual. Daher stimmen auch ihre Symmetriegruppen überein.

		winkeltreue Projektion in			mögliche Operationen
Dimension	Objekt	2-D	3-D	4-D	schieben	drehen	winden	stülpen
0	Punkt	+	+	+	–	–	–	–
1	Linie	+	+	+	+	–	–	–
2	Quadrat	+	+	+	+	+	–	–
3	Würfel	–	+	+	+	+	+	–
4	Tesserakt	–	–	+	+	+	+	+

Dimension	Kanten	Knoten	Seiten	Grad	Durchmesser	Kanten-Zusammenhang	Knoten-Zusammenhang
1
2
3
4
...	...	...	...	...	...	...	...
	$2^{{(n-1)}}\cdot n$	$2^{n}$

Siehe auch

Euklidischer Raum
Hilbertwürfel für den unendlichdimensionalen Fall
Hyperrechteck (alias Hyperquader) – Verallgemeinerung für unterschiedliche Kantenlängen
Hyperebene
Hyperraum

Basierend auf einem Artikel in:

Wikipedia.de