Euklidischer Raum
In der Mathematik ist der euklidische Raum zunächst der „Raum unserer Anschauung“, wie er in Euklids Elementen durch Axiome und Postulate beschrieben wird (vgl. euklidische Geometrie). Bis ins 19. Jahrhundert wurde davon ausgegangen, dass dadurch der uns umgebende physikalische Raum beschrieben wird. Der Zusatz „euklidisch“ wurde nötig, nachdem in der Mathematik allgemeinere Raumkonzepte (z.B. hyperbolischer Raum, riemannsche Mannigfaltigkeiten) entwickelt wurden und es sich im Rahmen der speziellen und allgemeinen Relativitätstheorie zeigte, dass zur Beschreibung des Raums in der Physik andere Raumbegriffe benötigt werden (Minkowski-Raum, Lorentz-Mannigfaltigkeit).
Im Laufe der Zeit wurde Euklids Geometrie auf verschiedene Arten präzisiert und verallgemeinert:
- axiomatisch durch Hilbert (siehe Hilberts Axiomensystem der euklidischen Geometrie),
- als euklidischer Vektorraum (einem über
definierten Vektorraum mit Skalarprodukt),
- als euklidischer Punktraum (einem affinen Raum, der über einem euklidischen Vektorraum modelliert ist),
- als Koordinatenraum
mit dem Standardskalarprodukt.
Wenn vom euklidischen Raum die Rede ist, dann kann jede dieser
Definitionen gemeint sein oder auch eine höherdimensionale Verallgemeinerung.
Den zweidimensionalen euklidischen Raum nennt man auch euklidische Ebene.
In diesem zweidimensionalen Fall wird der Begriff in der synthetischen
Geometrie etwas allgemeiner gefasst: Euklidische Ebenen können dort
als affine Ebenen über einer
allgemeineren Klasse von Körpern, den euklidischen
Körpern definiert werden. Diese Körper sind (je nach Auffassung) Teilkörper
oder isomorph zu Teilkörpern von
Vom affinen Raum unterscheidet sich der euklidische dadurch, dass man Längen und Winkel messen kann. Man zeichnet deshalb die Abbildungen aus, die Längen und Winkel erhalten. Diese nennt man traditionell Kongruenzabbildungen, andere Bezeichnungen sind Bewegungen und Isometrien.
In den nichteuklidischen Räumen, so dem hyperbolischen und dem elliptischen Raum, gilt das Parallelenaxiom nicht.
Euklidische Vektorräume
Vom euklidischen Anschauungsraum zum euklidischen Vektorraum
In der analytischen Geometrie ordnet man dem euklidischen Raum einen Vektorraum zu. Eine Möglichkeit, dies zu tun, ist, die Menge der Parallelverschiebungen (Translationen) zu nehmen, versehen mit der Hintereinanderausführung als Addition. Jede Verschiebung lässt sich durch einen Pfeil beschreiben, der einen Punkt mit seinem Bildpunkt verbindet. Dabei beschreiben zwei Pfeile, die gleichsinnig parallel sind und die gleiche Länge haben, dieselbe Verschiebung. Man nennt zwei solche Pfeile äquivalent und nennt die Äquivalenzklassen Vektoren.
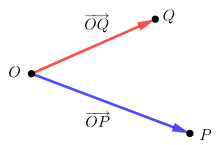
Wählt man im euklidischen Raum einen Punkt
als Bezugspunkt
(Ursprung)
aus, so kann man jedem Punkt
seinen Ortsvektor
zuordnen, den Vektor, der durch einen Pfeil vom Ursprung
zum Punkt
dargestellt wird. Auf diese Art bekommt man eine Eins-zu-eins-Beziehung zwischen
dem euklidischen Raum und dem zugehörigen euklidischen Vektorraum und kann so
den ursprünglichen euklidischen Raum mit dem euklidischen Vektorraum
identifizieren. Diese Identifizierung ist aber nicht kanonisch, sondern hängt
von der Wahl des Ursprungs ab.
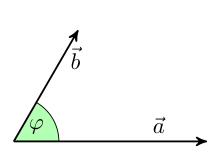
Man kann nun auch die Längen- und Winkelmessung aus dem euklidischen Raum auf
Vektoren übertragen als Länge der zugehörigen Pfeile und Winkel zwischen
solchen. Auf diese Art erhält man einen Vektorraum mit Skalarprodukt. Das
Skalarprodukt ist dadurch charakterisiert, dass das Produkt
eines Vektors
mit sich selbst das Quadrat
seiner Länge
ergibt. Aus den Rechengesetzen für Skalarprodukte, den binomischen Formeln
und dem Kosinussatz (angewandt auf
ein Dreieck, dessen Seiten den Vektoren
,
und
entsprechen) ergibt sich die Formel
.
Hierbei bezeichnet
den Winkel zwischen den Vektoren
und
.
Allgemeiner Begriff
Davon ausgehend nennt man jeden reellen Vektorraum mit Skalarprodukt
(beliebiger endlicher Dimension )
einen euklidischen Vektorraum. Man benutzt dann obige Formel, um Länge
(Norm)
eines Vektors und Winkel zwischen Vektoren zu definieren. Zwei Vektoren sind
dann orthogonal,
wenn ihr Skalarprodukt null ergibt. Jeder dreidimensionale euklidische
Vektorraum ist isometrisch isomorph zum Vektorraum der Pfeilklassen. Jeder
-dimensionale
euklidische Vektorraum ist isometrisch isomorph zum Koordinatenvektorraum
(siehe unten). Euklidische Vektorräume derselben Dimension
sind also nicht unterscheidbar. Dies berechtigt einen, jeden solchen als
den euklidischen Vektorraum der Dimension
zu bezeichnen. Manche Autoren benutzen den Begriff euklidischer Raum auch für
unendlichdimensionale reelle Vektorräume mit Skalarprodukt, manche auch für
komplexe Vektorräume mit Skalarprodukt, vgl. Skalarproduktraum.
Längen, Winkel, Orthogonalität und Orthonormalbasen
Sobald man einen reellen Vektorraum mit einem Skalarprodukt versehen hat,
kann man die metrischen Begriffe des euklidischen Anschauungsraums auf diesen
übertragen. Die Länge (die Norm,
der Betrag) eines Vektors
ist dann die Wurzel aus dem Skalarprodukt des Vektors mit sich selbst:
.
Zwei Vektoren
sind zueinander orthogonal
(oder senkrecht), wenn ihr Skalarprodukt null ist:
.
Den (nichtorientierten) Winkel zwischen zwei Vektoren definiert man mittels der obigen Formel
,
also
.
Ein Vektor
heißt Einheitsvektor,
wenn er die Länge 1 hat. Eine Basis
aus Einheitsvektoren, die paarweise orthogonal sind, heißt Orthonormalbasis.
In jedem euklidischen Vektorraum existieren Orthonormalbasen. Ist
eine Orthonormalbasis, so lässt sich der Vektor
in dieser Basis darstellen:
.
Die Koeffizienten erhält man durch
.
Isometrien
Sind
und
zwei
-dimensionale
euklidische Vektorräume, so nennt man eine lineare Abbildung
eine (lineare) Isometrie,
wenn sie das Skalarprodukt erhält, wenn also
für alle
gilt. Eine solche Abbildung
wird auch orthogonale
Abbildung genannt. Eine Isometrie erhält insbesondere Längen
und Winkel, also insbesondere Orthogonalität
Umgekehrt ist jede lineare Abbildung, die Längen erhält, eine Isometrie.
Eine Isometrie bildet jede Orthonormalbasis wieder auf eine Orthonormalbasis
ab. Umgekehrt, wenn
eine Orthonormalbasis von
ist und
eine Orthonormalbasis von
,
so gibt es genau eine Isometrie, die
auf
abbildet.
Daraus ergibt sich, dass zwei euklidische Vektorräume derselben Dimension isometrisch sind, also als euklidische Vektorräume nicht unterscheidbar sind.
Der euklidische Punktraum
Motivation
Euklidische Vektorräume dienen oft als Modelle für den euklidischen Raum. Die Elemente des Vektorraums werden dann je nach Kontext als Punkte oder Vektoren bezeichnet. Es wird nicht zwischen Punkten und ihren Ortsvektoren unterschieden. Rechnerisch kann dies von Vorteil sein. Begrifflich ist es jedoch unbefriedigend:
- Aus geometrischer Sicht sollten Punkte und Vektoren begrifflich
unterschieden werden.
- Vektoren können addiert und mit Zahlen multipliziert werden, Punkte aber nicht.
- Punkte werden durch Vektoren verbunden bzw. ineinander übergeführt.
- Im Vektorraum gibt es ein ausgezeichnetes Element, den Nullvektor. In der euklidischen Geometrie sind aber alle Punkte gleichberechtigt.
Beschreibung
Abhilfe schafft das Konzept des euklidischen Punktraums. Dies ist ein affiner Raum über einem euklidischen Vektorraum. Hier unterscheidet man Punkte und Vektoren.
- Die Gesamtheit der Punkte bildet den euklidischen Punktraum. Dieser wird
meist mit
,
,
oder
bezeichnet. (Das hochgestellte
ist kein Exponent, sondern ein Index, der die Dimension kennzeichnet.
ist also kein kartesisches Produkt.)
- Die Gesamtheit aller Vektoren bildet einen euklidischen Vektorraum
.
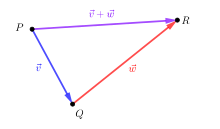
- Zu je zwei Punkten
und
existiert genau ein Verbindungsvektor, der mit
bezeichnet wird.
Der Verbindungsvektor eines Punktes mit sich selbst ist der Nullvektor: - Ein Punkt
kann durch einen Vektor
in eindeutiger Weise in einen Punkt
übergeführt werden. Dieser wird oft mit
bezeichnet. (Dies ist eine rein formale Schreibweise. Das Pluszeichen bezeichnet keine Vektorraumaddition, und auch keine Addition auf dem Punktraum.)
Der Nullvektor führt jeden Vektor in sich selbst über: - Führt der Vektor
den Punkt
in den Punkt
über und der Vektor
den Punkt
in den Punkt
, so führt
den Punkt
in den Punkt
über. Dies kann wie folgt ausgedrückt werden:
In der Sprache der Algebra
bedeuten diese Eigenschaften: Die additive Gruppe
des Vektorraums
operiert
frei und transitiv
auf der Menge
.
Längen, Abstände und Winkel
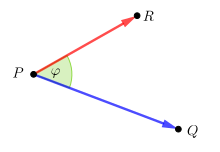
Streckenlängen, Abstände zwischen Punkten, Winkel und Orthogonalität können nun mit Hilfe des Skalarprodukts von Vektoren definiert werden:
Die Länge
der Strecke
und den Abstand
der Punkte
und
definiert man als die Länge des Vektors
:
Die Größe des Winkels
definiert man als den Winkel zwischen den Vektoren
und
:
Zwei Strecken
und
sind genau dann orthogonal, wenn die zugehörigen Vektoren
und
orthogonal sind.
Abbildungen
Längenerhaltende Abbildungen eines euklidischen Punktraums auf sich heißen Isometrien,
Kongruenzabbildungen
(in der ebenen Geometrie) oder Bewegungen.
Sie erhalten automatisch auch Winkel. Ist
eine Bewegung, so existiert eine orthogonale Abbildung (lineare Isometrie)
,
so dass für alle Punkte
und
gilt:
Der reelle Koordinatenraum
Definition
Der -dimensionale
reelle Koordinatenraum
ist das
-fache
kartesische
Produkt der Menge
der reellen Zahlen, also die Menge der
-Tupel
wobei die
reelle Zahlen sind. Man bezeichnet die Elemente des
je nach Kontext als Punkte oder als Vektoren, es wird also nicht zwischen
Punkten und Vektoren unterschieden.
Als Vektoren werden sie komponentenweise addiert und mit reellen Zahlen multipliziert:
In diesem Fall werden die Elemente des
oft als Spaltenvektoren (d.h.
-Matrizen)
geschrieben:
Das Skalarprodukt (Standardskalarprodukt) ist definiert durch
.
Mit diesem Skalarprodukt ist der
ein euklidischer Vektorraum.
Vom euklidischen Vektorraum/Punktraum zum Koordinatenraum
Wählt man in einem euklidischen Vektorraum eine Orthonormalbasis bzw.
in einem euklidischen Punktraum ein kartesisches
Koordinatensystem (d.h. einen Koordinatenursprung
und eine Orthonormalbasis des Vektorraums), so wird dadurch jedem Vektor bzw.
Punkt ein Koordinaten--Tupel
zugeordnet. Auf diese Art erhält man eine Isometrie zwischen dem gegebenen
euklidischen Raum und dem Koordinatenraum und kann diese vermöge dieser
Isometrie miteinander identifizieren. Dies rechtfertigt es, den
als den euklidischen Raum zu bezeichnen. Die Isometrie hängt jedoch von
der Wahl der Orthonormalbasis und – im Fall des Punktraums – von der Wahl des
Ursprungs ab.
Länge, Winkel, Orthogonalität, Standardbasis und Abstände
Die Länge oder Norm eines Vektors ist wie in jedem euklidischen Vektorraum durch die Quadratwurzel aus dem Skalarprodukt mit sich selbst gegeben:
Man nennt diese Norm auch euklidische
Norm oder 2-Norm
und schreibt statt
auch
oder
.
Der Winkel zwischen zwei Vektoren
und
berechnet sich dann durch
Zwei Vektoren
und
sind genau dann orthogonal,
,
wenn
gilt. Die Vektoren der Standardbasis
sind Einheitsvektoren und paarweise orthogonal, bilden also eine Orthonormalbasis.
Fasst man die Elemente des
als Punkte auf, so ist der Abstand zwischen den Punkten
und
als die Länge des Verbindungsvektors
definiert:
Isometrien
Vektorraum-Isometrien (lineare Isometrien) des
sind orthogonale
Abbildungen, die durch orthogonale
Matrizen dargestellt werden. Ist
eine lineare Isometrie und ist
das Bild des -ten
Standardbasisvektors (
),
so lässt sich
mit Hilfe der Matrizenmultiplikation
darstellen als
.
Jede Isometrie (Bewegung)
des Punktraums
lässt sich in der Form
als Verknüpfung einer orthogonalen Abbildung
und einer Parallelverschiebung
(Translation)
darstellen.
Orientierung
Jeder endlichdimensionale reelle Vektorraum kann durch die Wahl einer geordneten
Basis mit einer Orientierung
versehen werden. Während bei beliebigen euklidischen Vektor- und Punkträumen
keine Orientierung ausgezeichnet ist, besitzt der Koordinatenraum
eine kanonische Orientierung, die durch die Standardbasis gegeben ist: Die
geordnete Basis aus den Vektoren
ist positiv orientiert.
Eine geordnete Basis
ist genau dann positiv orientiert, wenn die aus ihr gebildete Determinante positiv ist:
Identifiziert man den (als euklidisch angenommenen) physikalischen Raum mit
dem Koordinatenraum ,
indem man ein kartesisches
Koordinatensystem einführt, so wählt man die Koordinatenachsen üblicherweise
so, dass sie ein Rechtssystem
bilden. Die durch die Rechte-Hand-Regel
gegebene Orientierung des physikalischen Raums entspricht dann der kanonischen
Orientierung des Koordinatenraums
.
Der euklidische Raum in anderen Gebieten der Mathematik
Euklidische Räume in der Topologie

Die Funktion, die jedem Vektor seine durch das Skalarprodukt definierte Länge
zuordnet, ist eine Norm.
Man spricht von der durch das Skalarprodukt induzierten Norm oder der Skalarproduktnorm;
manche Autoren nennen die Norm auch euklidische Norm. Die durch das
Standardskalarprodukt auf
induzierte Norm heißt euklidische
Norm oder 2-Norm und ist ein Spezialfall der p-Normen.
Durch die induzierte Norm wird jeder euklidische Vektorraum zu einem normierten Raum und
dadurch zum klassischen Beispiel eines topologischen
Vektorraums. Insbesondere ist er ein Prähilbertraum
und, weil dieser im Endlichdimensionalen auch vollständig
ist, ein Banachraum und somit auch
ein Hilbertraum.
Durch die euklidische
Abstandsfunktion
wird jeder euklidische Raum zu einem metrischen
Raum und damit insbesondere zu einem topologischen
Raum.
Da auf endlichdimensionalen Vektorräumen alle Normen äquivalent
sind, hängt die Topologie des euklidischen Raums in Wirklichkeit nicht von der
euklidischen Struktur ab. Normierte Vektorräume derselben endlichen Dimension
sind also alle zueinander homöomorph
und damit homöomorph zum
.
Nach dem Satz
von der Invarianz der Dimension von Luitzen E. J. Brouwer sind euklidische Räume verschiedener Dimension jedoch nicht
homöomorph aufeinander abbildbar.
Als topologischer Raum ist der euklidische Raum zusammenhängend und zusammenziehbar.
Euklidische Räume in der Differentialtopologie
Mannigfaltigkeiten werden über euklidischen Räumen modelliert: Eine
Mannigfaltigkeit ist lokal homöomorph zum .
Durch die differenzierbare Struktur sind differenzierbare
Mannigfaltigkeiten lokal diffeomorph
zum
.
Insbesondere ist der euklidische Raum selbst eine differenzierbare
Mannigfaltigkeit. Für alle Dimensionen außer Dimension vier ist eine zu
homöomorphe differenzierbare Mannigfaltigkeit auch zu
diffeomorph. Die in vier Dimensionen bestehenden Ausnahmen werden exotische
4-Räume genannt.
Euklidische Räume in der Differentialgeometrie
Durch das (nicht vom Punkt abhängige) Skalarprodukt wird der euklidische Raum
zu einer riemannschen
Mannigfaltigkeit. Umgekehrt wird in der riemannschen
Geometrie jede riemannsche Mannigfaltigkeit, die isometrisch zum Vektorraum
mit dem Standardskalarprodukt
ist, als euklidischer Raum bezeichnet. Für diese riemannschen Mannigfaltigkeiten
verschwindet der Krümmungstensor,
das heißt, der Raum ist flach. Umgekehrt ist jede flache riemannsche
Mannigfaltigkeit lokal isometrisch zum euklidischen Raum. Es kann sich
allerdings auch um eine offene Teilmenge eines
handeln oder um eine Mannigfaltigkeit, deren universelle
Überlagerung eine Teilmenge des
ist. Zweidimensionale Beispiele für den letzten Fall sind ein flacher Torus oder
ein gerader Kreiszylinder.
Hingegen ist jede vollständige und einfach zusammenhängende flache riemannsche
Mannigfaltigkeit ein euklidischer Raum.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 12.06. 2020