Schiefer Kegel

Schiefkegel

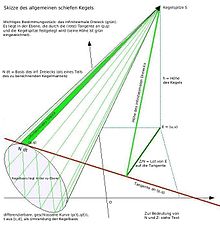
Die Basis des allgemeinen Schiefkegels ist eine geschlossene Kurve mit der Parameter-Darstellung x(t):= p(t) und y(t):= q(t), wobei p und q im Intervall [c,d] differenzierbar sind (bis auf höchstens endlich viele Ausnahmen), außerdem: p(c) = p(d) und q(c) = q(d). Der Punkt E = (u,v) liegt in der Kurven-Ebene, die Kegelspitze S steht im Abstand h senkrecht über E, also S = (u,v,h). Der folgende Formalismus gilt auch für nicht geschlossene Kurven, dann spricht man besser von Segeln als von Kegeln (Dreiecks-Segeln, geschwungenen Dreiecken). Um die Formeln übersichtlich zu halten, wird die Ableitung nach t (wie in der Physik üblich) mit einem Punkt versehen.

Mantel des allgemeinen Schiefkegels

Die Formel für die Mantelfläche M des allgemeinen Schiefkegels gleicht der des schiefen Ellipsenkegels (abgesehen von den Integrationsgrenzen):

$M={\frac {1}{2}}\int \limits _{c}^{d}{\sqrt {Z(t)^{2}+h^{2}\cdot N(t)^{2}}}\mathrm {d} t$

Hier bedeuten

$Z(t)=(p-u)\cdot {\dot {q}}-(q-v)\cdot {\dot {p}}$

und

$N(t)={\sqrt {{\dot {p}}^{2}+{\dot {q}}^{2}}}$

Man könnte mit diesem Formalismus auch den Pyramiden-Mantel berechnen (die Pyramide als „Kegel“ mit quadratischer Basis), aber hier führt die Elementar-Geometrie schneller zum Ziel.

Die geometrische Bedeutung von Z und N

Von Z

Das Radizieren einer Funktion f über [c,d] erfordert Sorgfalt, denn die Quadratwurzel aus f² ist mehrdeutig, sogar unendlich vieldeutig. Um das einzusehen, braucht man nur an einer beliebigen Stelle a (die nicht Nullstelle von f ist) den Wert f(a) in -f(a) umzukehren. Geometrisch bedeutsam sind die Wurzeln |f| und f. Wenn in der Formel für den Mantel eines allgemeinen Schiefkegels die Höhe h gegen Null strebt, entsteht der Ausdruck

$M={\frac {1}{2}}\int \limits _{c}^{d}{\sqrt {Z(t)^{2}}}\mathrm {d} t$

und insbesondere für die Wurzel |Z(t)|:

$M={\frac {1}{2}}\int \limits _{c}^{d}|Z(t)|\mathrm {d} t$

geometrisch gesehen ist das die Fläche des „zusammengefalteten“ Kegelmantels in der xy-Ebene (wo die Kegelbasis liegt). Für die Wurzel Z(t) hingegen ergibt sich

$M={\frac {1}{2}}\int \limits _{c}^{d}Z(t)\mathrm {d} t={\frac {1}{2}}\int \limits _{c}^{d}((p-u)\cdot {\dot {q}}-(q-v)\cdot {\dot {p}})\mathrm {d} t={\frac {1}{2}}\int \limits _{c}^{d}(p{\dot {q}}-{\dot {p}}q)\mathrm {d} t$

weil die bestimmten Integrale über die Ableitungen von uq und vp Null sind. Das folgt aus der Nebenbedingung p(c) = p(d) und q(c) = q(d). Geometrisch gesehen handelt es sich hierbei um die Fläche der Kegelbasis. Durch partielle Integration (und Beachtung von p(c)q(c) = p(d)q(d)) gewinnt man die Gleichung:

$M={\frac {1}{2}}\int \limits _{c}^{d}(p{\dot {q}}-{\dot {p}}q)\mathrm {d} t=\int \limits _{c}^{d}p{\dot {q}}\mathrm {d} t$

Der rechte Ausdruck besticht durch seine Kürze, ist aber unpraktisch, weil sich der scheinbar komplizierte linke Ausdruck besser auswerten lässt. Die Fläche zwischen den Tangenten von E an die Kegelbasis (die Basis selbst nicht mitgerechnet), also die Fläche des Tangenten-Zipfels, ergibt sich aus

$M={\frac {1}{4}}\int \limits _{c}^{d}(|Z(t)|-Z(t))\mathrm {d} t$

Der Faktor ¼ (statt ½) besagt, dass die Fläche des Tangentenzipfels nur einmal gezählt wird (statt doppelt wie beim zusammengefalteten Kegelmantel, bei dem die E zugewandte und die E abgewandte Mantelfläche übereinander liegen). Wenn E auf dem Rand oder innerhalb der Kegelbasis liegt, verschwindet M. Dann nämlich fallen Basis und zusammengefalteter Mantel in eins.

Von N

Ndt ist das Integrationselement des Umfangs der Kegelbasis (siehe Grafik). Der Umfang der Kegelbasis ergibt sich daher zu

$U=\int \limits _{c}^{d}|N(t)|\mathrm {d} t$

Wenn man nur N(t) als Integranden wählt (statt |N(t)|), kann es vorkommen, dass das Integral verschwindet. Beispiel: Die Astroide (Sternkurve) hat die Parameterdarstellung p(t) = a cos(t)³, q(t) = a sin(t)³ über [0, $2\Pi$ ]. Dann ist N(t)² = 9a² sin(t)² cos(t)². Für N(t) = 3a sin(t) cos(t) verschwindet das Integral über [0, $2\Pi$ ]. Für |N(t)| jedoch ergibt sich

$U=3a\int \limits _{0}^{2\pi }\left|\sin(t)\cdot \cos(t)\right|\mathrm {d} t=12a\int \limits _{0}^{\frac {\pi }{2}}\sin(t)\cdot \cos(t)\mathrm {d} t=6a$

Von Z/N

Der Quotient misst den Abstand des Höhenfußpunktes E = (u,v) von der Kurven-Tangente an (p,q) in Abhängigkeit von t (siehe Grafik). Die allgemeine Gleichung der Tangente an (p,q) lautet

$(p-x)\cdot {\dot {q}}-(q-y)\cdot {\dot {p}}=0$

Division durch N führt zur Hesseschen Normalform. Den Abstand des Punktes E = (u,v) von der Tangente gewinnt man dadurch, dass man u und v in die Normalform einsetzt (ohne die Null): das Ergebnis ist Z/N. Beispiel: Die Funktionen p(t) = r cos(t) + m und q(t) = r sin(t) + n über [0, $2\Pi$ ] beschreiben den Kreis r um (m,n). Dann ist Z(t)/N(t) = r + (m-u) cos(t) + (n-v) sin(t). Wenn E in das Zentrum des Kreises rückt, wenn also u = m und v = n, resultiert Z(t)/N(t) = r, d.h. die Lote von E auf die Kreistangenten sind die Radiusvektoren der Länge r.

Beispiel: Schiefer Kreiskegel

Die Parameterdarstellung des Kreises lautet: $p(t)=r\cos(t),q(t)=r\sin(t)$ über $[0,2\pi]$ .

Wenn man diese Werte und ihre Ableitungen in die Formel für den Mantel des allgemeinen Schiefkegels einsetzt, erhält man den Ausdruck

$M={\frac {r}{2}}\int \limits _{0}^{2\pi }{\sqrt {(r-u\cdot \cos(t)-v\cdot \sin(t))^{2}+h^{2}}}\mathrm {d} t$

Mit einem geeigneten (festen) Winkel lassen sich und darstellen als $u=e\cos(w)$ und $v=e\sin(w)$ , wobei $e^{2}:=u^{2}+v^{2}$ , daher gilt nach dem Additionstheorem: $u\cos(t)+v\sin(t)=e\cos(w-t)$ , so dass

$M={\frac {r}{2}}\int \limits _{0}^{2\pi }{\sqrt {(r-e\cdot \cos(w-t))^{2}+h^{2}}}\mathrm {d} t$

Bei der Integration über den Vollkreis spielt die Wahl von keine Rolle. Man darf deshalb $w=0$ setzen. Der Integrand ist für $w=0$ eine bezüglich $\pi$ symmetrische Funktion, so dass man nur über den Halbkreis zu integrieren braucht und das Resultat verdoppeln muss, also:

$M=r\int \limits _{0}^{\pi }{\sqrt {(r-e\cdot \cos(t))^{2}+h^{2}}}\mathrm {d} t$ .

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de