Schiefer Kreiskegel
Beim geraden Kreiskegel
steht die Spitze
senkrecht
über dem Zentrum
des Grundkreises mit dem Radius
,
beim schiefen Kreiskegel (siehe Zeichnung) senkrecht über einem von
verschiedenen Punkt
der Kreisebene.
Die Entfernung („Abweichung“) des
Punktes
vom Kreismittelpunkt sei
.
Die Höhe
ist der Abstand zwischen
und der Kreisebene (beim geraden Kreiskegel die Strecke
,
beim schiefen die Strecke
).
Als Mantel
eines Kreiskegels bezeichnet man seine Oberfläche ohne die Fläche des
Grundkreises. Zugunsten einer bequemen Sprechweise werden Strecke und
Streckenlänge, Mantel und Mantelfläche usw. identifiziert. Kreiskegel derselben
Höhe über demselben Grundkreis haben dasselbe Volumen
(das folgt aus dem Cavalierischen
Prinzip). Der Mantel des geraden Kreiskegels lässt sich elementar
berechnen:
,
wobei
.
Es gibt keine ähnlich einfache Formel für den Mantel des schiefen Kreiskegels.
Kegelmantel
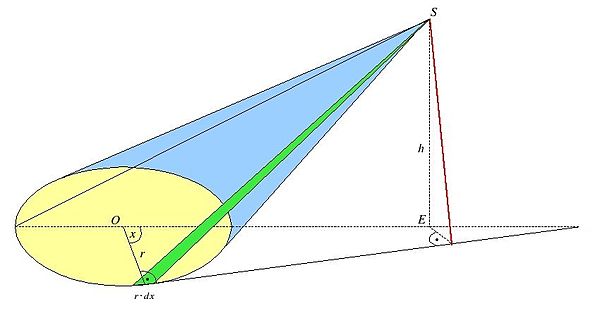
Den Mantel des schiefen Kreiskegels erhält man durch Integration. Das infinitesimale Dreieck (in der Zeichnung grün unterlegt) hat die Basis
wobei
der Winkel im
Mittelpunkt des Kreises ist, und die Höhe (rote Strecke in der Zeichnung)
mithin die Fläche
Da
symmetrisch
um
liegt, genügt es, von 0 bis
zu integrieren und das Ergebnis zu verdoppeln. Daher lautet die Formel für den
Mantel
des schiefen Kreiskegels
.
Man kann im Integranden das Minus durch ein Plus ersetzen, ohne den Wert des
Integrals zu ändern (wenn man über den Vollkreis integriert, darf man sogar den
Kosinus
gegen den Sinus tauschen). Der Ausdruck berücksichtigt den geraden Kreiskegel
als Sonderfall und liefert für
die bekannte Formel. Durch geeignete Wahl einer oberen und unteren Schranke des
Integranden lässt sich der Mantel nach oben und unten abschätzen. Aus der
Schätzung des Intervalls folgt, wenn
unter einer festen Schranke bleibt,
für
.
Wenn also die Abweichung groß gegenüber Radius und Höhe ist, gilt
näherungsweise
(Durchmesser mal Abweichung). Beispiel: Der Mantel des schiefen Kreiskegels vom
Radius 2 cm, der Höhe 6 cm und der Abweichung 50 cm hat eine
Fläche von 205,92… cm2, also ungefähr 2 mal 2 mal
50 cm2 (wäre die Höhe nur halb so groß, ergäbe sich ein Mantel
von 201,85… cm2).
Extremalwertsätze
Unter allen Kreiskegeln derselben Höhe über demselben Grundkreis besitzt der gerade den kleinsten Mantel (und damit die kleinste Oberfläche).
Denn wenn man den Mantel und den Integranden als Funktionen von
auffasst, wenn also
dann ist
Nach der partiellen
Ableitung des Integranden
erkennt man, dass
für
und sonst
(außerdem
).
ist also monoton
steigend (der Mantel wird größer mit wachsender Abweichung). Die Strecke
heißt Achse des Kreiskegels. Wenn die Achse eine konstante Länge beibehält, wenn
also
(
fest) und damit
,
dann gilt wieder
für
,
nun aber ist
,
hat bei
ein Maximum. Deshalb gilt der Satz:
Unter allen Kreiskegeln derselben Achse über demselben Grundkreis besitzt der gerade den größten Mantel (und damit die größte Oberfläche).
Beziehung zwischen geradem Ellipsen- und schiefem Kreiskegel
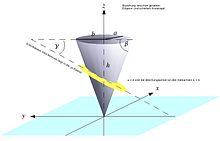
Ein gerader Ellipsenkegel mit der Höhe
und der Ellipse
als Basis ()
wird durch die folgende Gleichung beschrieben:
Alle Werte ,
die
erfüllen (
),
liegen auf dem Mantel des geraden Ellipsenkegels, dessen Spitze der Nullpunkt
ist (siehe Zeichnung).
sei der minimale Böschungswinkel (
)
und
der maximale (
),
also
.
Eine Ebene, deren Normale in der yz-Ebene
liegt und die mit der xy-Ebene
den Winkel
bildet, wobei
ist, schneidet den geraden Ellipsenkegel in einem Kreis. Sein Radius
beträgt
dabei bedeutet
den Abstand der Schnittebene von der Kegelspitze (Lot auf die Ebene), ggf. muss
man sich den Kegel über die Basis hinaus verlängert denken, um den Kreisschnitt
ganz ausführen zu können. Der Restkegel zwischen Spitze und (in der Zeichnung
gelb angedeuteter) Schnittfläche ist also ein schiefer Kreiskegel. Jeder gerade
Ellipsenkegel enthält einen schiefen Kreiskegel und umgekehrt: Jeder schiefe
Kreiskegel lässt sich zu einem geraden Ellipsenkegel erweitern.
Siehe auch
- Schiefer Ellipsenkegel
- Schiefer Kegel (allgemein)


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.05. 2021