Satz von Qvist

Satz von Qvist über endliche Ovale

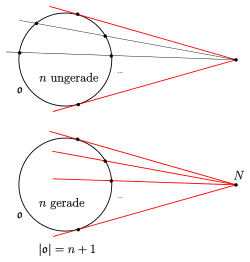
Der Satz von Qvist, benannt nach dem finnischen Mathematiker Bertil Qvist, macht eine Aussage über Ovale in einer endlichen projektiven Ebene. Standardbeispiele von Ovalen sind die nicht ausgearteten (projektiven) Kegelschnitte. Der Satz gibt an, wie viele Tangenten an ein vorgegebenes Oval durch einen gegebenen Punkt gehen können. Die Antwort hängt wesentlich davon ab, ob die Ordnung (Anzahl der Punkte auf einer Gerade -1) der projektiven Ebene gerade oder ungerade ist. Der Satz bietet im pappusschen Fall gerader Ordnung über den Begriff Hyperoval eine einfache Möglichkeit, Ovale anzugeben, die keine Kegelschnitte sind. (Im pappusschen Fall ungerader Ordnung sind alle Ovale schon Kegelschnitte (Satz von Segre).)

Definition eines Ovals

→ Hauptartikel: Oval (Projektive Geometrie)

Eine Menge ${\mathfrak {o}}$ von Punkten in einer projektiven Ebene heißt Oval, wenn

(1) Eine beliebige Gerade trifft ${\mathfrak {o}}$ in höchstens 2 Punkten.
Falls $|g\cap {\mathfrak {o}}|=0$ ist, heißt Passante, falls $|g\cap {\mathfrak {o}}|=1$ ist, heißt Tangente und falls $|g\cap {\mathfrak {o}}|=2$ ist, heißt Sekante.

(2) Zu jedem Punkt $P\in {\mathfrak {o}}$ gibt es genau eine Tangente

, d.h. $t\cap {\mathfrak {o}}=\{P\}$ .

Für endliche projektive Ebenen (d.h. die Punktmenge und Geradenmenge sind endlich) gilt

In einer projektiven Ebene der Ordnung (d.h. jede Gerade enthält $n+1$ Punkte) ist eine Menge ${\mathfrak {o}}$ genau dann ein Oval, wenn $|{\mathfrak {o}}|=n+1$ ist und keine drei Punkte von ${\mathfrak {o}}$ kollinear (auf einer Gerade) liegen.

Aussage und Beweis des Satzes von Qvist

Satz von Qvist

${\mathfrak {o}}$ sei ein Oval in einer endlichen projektiven Ebene der Ordnung .

(a) Falls ungerade ist, gilt:

Jeder Punkt $P\notin {\mathfrak {o}}$ inzidiert mit $0$ oder Tangenten.

(b) Falls gerade ist, gilt:

Es gibt einen Punkt , den Nukleus oder Knoten, so, dass die Menge der Tangenten an ${\mathfrak {o}}$ gleich dem Geradenbüschel von ist.

Satz von Qvist: Zum Beweis im Fall n ungerade

Satz von Qvist: zum Beweis im Fall n gerade

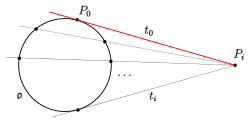
Beweis

(a) Es sei $P\in {\mathfrak {o}}$ und $t_{0}$ die Tangente in $P_{0}$ und $t_{0}=\{P_{0},P_{1},...,P_{n}\}$ . Die Geraden durch $P_{i},i\neq 0$ zerlegen ${\mathfrak {o}}$ in Teilmengen der Mächtigkeit 2 oder 1 oder 0. Da $|{\mathfrak {o}}|=n+1$ gerade ist, gibt es durch jeden Punkt $P_{i},i\neq 0$ eine weitere Tangente $t_{i}$ . Die Anzahl der Tangenten ist n+1 . Also gehen durch $P_{i},i\neq 0,\;$ genau zwei Tangenten, nämlich $t_{0}$ und $t_{i}$ .

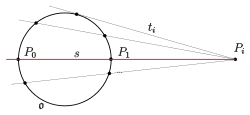
(b) Es sei eine Sekante, $s\cap {\mathfrak {o}}=\{P_{0},P_{1}\}$ und $s=\{P_{0},P_{1},...,P_{n}\}$ . Da $|{\mathfrak {o}}|=n+1$ ungerade ist, muss es durch $P_{i}$ für $i=2,...,n$ wenigstens eine Tangente $t_{i}$ geben. Die Anzahl der Tangenten ist n+1 . Also geht durch jeden Punkt $P_{i}$ für $i=2,...,n$ genau eine Tangente. Ist der Schnittpunkt zweier Tangenten, so kann mit keiner Sekanten inzidieren. Wegen $|{\mathfrak {o}}|=n+1$ ist jede Gerade durch den Punkt eine Tangente.

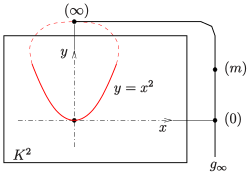
Beispiel pappussche Ebene gerader Ordnung

In inhomogenen Koordinaten über einem Körper $K,|K|=n$ gerade, ist

${\mathfrak {o}}_{1}=\{(x,y)\;|\;y=x^{2}\}\;\cup \{(\infty )\}$

(projektiver Abschluss der Normparabel) ein Oval mit dem Fernpunkt $N=(0)$ als Nukleus (s. Bild unten), d.h. jede Gerade $y=c,\;c\in K\;,$ ist Tangente. (Das Quadrieren ist im geraden Fall eine Bijektion !)

Definition und Eigenschaft eines Hyperovals

Ist ${\mathfrak {o}}$ ein Oval in einer endlichen projektiven Ebene gerader Ordnung , so besitzt ${\mathfrak {o}}$ einen Knoten .

Man nennt die Punktmenge ${\mathfrak {\bar {o}}}:={\mathfrak {o}}\cup \{N\}$ ein Hyperoval oder (n+2)-Bogen. (Ein endliches Oval ist ein (n+1)-Bogen).

Eine wesentliche Eigenschaft eines Hyperovals ist

Ist ${\mathfrak {\bar {o}}}$ ein Hyperoval und $R\in {\mathfrak {\bar {o}}}$ , so ist ${\mathfrak {\bar {o}}}\setminus \{R\}$ ein Oval.

projektiver Kegelschnitt ${\mathfrak {o}}_{1}$

Diese Eigenschaft bietet eine einfache Möglichkeit zu einem Oval weitere Ovale anzugeben.

Beispiel

In der projektiven Ebene über dem Körper $K,|K|=n$ gerade und n>4 , ist

${\mathfrak {o}}_{1}=\{(x,y)\;|\;y=x^{2}\}\;\cup \{(\infty )\}$ ein Oval (Kegelschnitt) (s. Bild),

${\mathfrak {\bar {o}}}_{1}=\{(x,y)\;|\;y=x^{2}\}\;\cup \{(0),(\infty )\}$ ein Hyperoval und

${\mathfrak {o}}_{2}=\{(x,y)\;|\;y=x^{2}\}\;\cup \{(0)\}$ ein weiteres Oval, das kein Kegelschnitt ist. (Ein Kegelschnitt ist durch 5 Punkte eindeutig bestimmt !)

Literatur

Bertil Qvist: Some remarks concerning curves of the second degree in a finite plane. In: Ann. Acad. Sci Fenn. Nr. 134, Helsinki (1952), S. 1–27.
Albrecht Beutelspacher, Ute Rosenbaum: Projektive Geometrie. 2. Auflage. Vieweg, Wiesbaden 2004, ISBN 3-528-17241-X.
Peter Dembowski: Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8.

Basierend auf einem Artikel in:

Wikipedia.de