Quasikonvexe Funktion

Eine quasikonvexe Funktion, die nicht konvex ist.

Eine Funktion, die nicht quasikonvex ist: Die Menge der Punkte, für die die Funktionswerte unterhalb der gestrichelten roten Linie liegen, ist die Vereinigung von zwei getrennten Intervallen und daher nicht konvex.

Eine quasikonvexe Funktion ist eine reellwertige Funktion, die auf einer konvexen Teilmenge eines reellen Vektorraums definiert ist und die Eigenschaft konvexer Funktionen verallgemeinert, dass alle ihre Subniveaumengen konvex sind. Ähnlich wie bei den konvexen Funktionen definiert man als Gegenstück die quasikonkave Funktion. Ist eine Funktion quasikonvex und quasikonkav, so heißt sie eine quasilineare Funktion. Quasikonvexe Funktionen sind von Bedeutung bei verschiedenen Anwendungen in der Wirtschaftstheorie. Optimierungsmethoden, die auf die Klasse der quasikonvexen Funktionen zugeschnitten sind, gehören zur quasikonvexen Optimierung und sind Verallgemeinerungen der konvexen Optimierung.

Definition

Quasikonvexe Funktionen können auf zwei Arten definiert werden. Je nach Wahl der Definition wird die andere Definition dann als Eigenschaft aufgeführt.

Über Niveaumengen

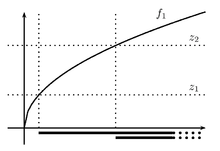
Der Graph einer quasikonkaven Funktion.

Eine Funktion $f\colon S\to \mathbb {R}$ , die auf einer konvexen Teilmenge S eines reellen Vektorraums definiert ist, heißt

quasikonvex, wenn jede Subniveaumenge

$\mathcal L^\leq_f(c) := \{x \in S \mid f(x) \leq c\}$

für beliebiges $c\in \mathbb{R}$ konvex ist.

quasikonkav, wenn jede Superniveaumenge

$\mathcal L^\geq_f(c) := \{x \in S \mid f(x) \geq c\}$

für beliebiges $c\in \mathbb{R}$ konvex ist. Äquivalent dazu ist, dass

quasikonvex ist.

quasilinear, wenn sie sowohl quasikonvex als auch quasikonkav ist.

Über Ungleichungen

Eine Funktion $f\colon S\to \mathbb {R}$ , die auf einer konvexen Teilmenge S eines reellen Vektorraums definiert ist, heißt

quasikonvex, wenn aus $x,y\in S$ und $\lambda \in [0,1]$ folgt, dass

$f(\lambda x + (1 - \lambda)y)\leq\max\{f(x),f(y)\}.$

strikt quasikonvex, wenn

$f(\lambda x + (1 - \lambda)y)<\max\{f(x),f(y)\}$

für alle $x\neq y$ und $\lambda \in (0,1)$ gilt.

quasikonkav, wenn aus $x,y\in S$ und $\lambda \in [0,1]$ folgt, dass

$f(\lambda x + (1 - \lambda)y)\geq\min\{f(x),f(y)\}.$

strikt quasikonkav, wenn

$f(\lambda x + (1 - \lambda)y)>\min\{f(x),f(y)\}$

für alle $x\neq y$ und $\lambda \in (0,1)$ gilt.

Äquivalent zur (strikten) Quasikonkavität von ist, dass (strikt) quasikonvex ist. Die Quasilinearität wird wie oben definiert: Eine Funktion heißt quasilinear, wenn sie quasikonvex und quasikonkav ist.

Beispiele

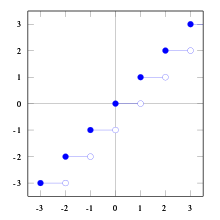
Abrundungsfunktion oder Gaußklammerfunktion

Jede konvexe Funktion ist quasikonvex, da die Subniveaumengen von konvexen Funktionen konvex sind.
Analog sind alle konkaven Funktionen quasikonkav.
Jede monotone Funktion ist sowohl quasikonvex als auch quasikonkav, also quasilinear.
Die Abrundungsfunktion $x\mapsto \lfloor x\rfloor$ ist das Beispiel einer quasikonvexen Funktion, die weder konvex noch stetig ist.
Lineare Funktionen sind quasilinear.
$\mathbb {R} \rightarrow \mathbb {R} ,\,x\mapsto x^{+}:=\mathrm {max} (x,0)$ ist nicht linear, aber quasilinear.

Eigenschaften

Stetige quasikonvexe Funktionen auf einem normierten Vektorraum sind immer schwach unterhalbstetige Funktionen.
Daher nehmen stetige quasikonvexe Funktionen auf schwach folgenkompakten Mengen ein Minimum an.
Speziell nehmen demnach stetige quasikonvexe Funktionen auf einer konvexen, abgeschlossenen, beschränkten und nichtleeren Teilmenge eines reflexiven Banachraumes ein Minimum an.
Eine stetige Funktion $f:D\mapsto {\mathbb {R}}$ mit $D\subset {\mathbb {R}}$ konvex ist genau dann quasikonvex, wenn mindestens eine der drei folgenden Bedingungen gilt:

ist monoton wachsend auf .
ist monoton fallend auf .
Es gibt ein $t\in D$ , so dass für für alle $x\leq t$ monoton fallend ist und für alle $x\geq t$ monoton wachsend ist.

Der Definitionsbereich und jede Niveaumenge einer quasilinearen Funktion sind konvex.
Wie bei konvexen Funktionen gilt, dass eine Funktion $f\colon V\supset D\to \mathbb {R}$ , wobei eine konvexe Menge ist, genau dann quasikonvex ist, wenn die Funktion $g\colon \mathbb {R} \to \mathbb {R}$ definiert durch quasikonvex ist für alle $x \in D$ und alle Richtungen .

Rechenregeln

Punktweise positiv gewichtete Maxima

Sind $f_{i}$ quasikonvexe Funktionen und $w_i \geq 0$ positive reelle Zahlen für $i=1,\dots ,n$ , dann ist auch

$g(x)= \max \{w_1 f_1(x), \dots, w_n f_n (x)\}$

eine quasikonvexe Funktion. Dies folgt aus der der Tatsachen, dass die Subniveaumenge der Funktion genau der Schnitt aller Subniveaumengen der Funktionen $f_{i}$ ist. Diese sind aber per Definition konvex und damit ist die Niveaumenge von als Schnitt konvexer Mengen auch konvex.

Punktweises Supremum

Ist f(x,y) eine quasikonvexe Funktion in für alle $y\in D$ und ist $w(y) \geq 0$ für alle $y\in D$ , so ist auch

$g(x)=\sup_{y \in D}(w(y)f(x,y))$

eine quasikonvexe Funktion. Dies lässt sich analog zeigen wie der Fall mit Maxima.

Punktweises Infimum

Ist f(x,y) quasikonvex sowohl in als auch in und ist $y \in C$ wobei eine konvexe Menge ist, so ist die Funktion

$g(x)=\inf_{y \in C} f(x,y)$

quasikonvex.

Komposition

Ist $f\colon \mathbb {R} ^{n}\to \mathbb {R}$ quasikonvex und ist $g\colon \mathbb {R} \to \mathbb {R}$ eine monoton fallende Funktion, so ist h(x)=g(f(x)) eine quasikonvexe Funktion.

Quasikonvexität und Differenzierbarkeit

Unter Verwendung der ersten Ableitung

Gegeben sei die differenzierbare Funktion $f:D\mapsto {\mathbb {R}}$ mit $D\subset \mathbb {R} ^{n}$ konvex. Dann ist die genau dann quasikonvex, wenn für alle $x,y\in D$ gilt, dass

$f(y)\leq f(x)\implies \nabla f(x)^{T}(y-x)\leq 0$ .

Im Falle einer Funktion auf den reellen Zahlen vereinfacht sich dies zu

$f(y)\leq f(x)\implies f'(x)y\leq f'(x)x$ .

Aufgrund der Äquivalenz wird dieses auch gelegentlich zur Charakterisierung von Quasikonvexität genutzt.

Im Gegensatz zu konvexen Funktionen folgt bei quasikonvexen Funktionen aus $\nabla f(\tilde x)=0$ bzw. $f'({\tilde {x}})=0$ im Allgemeinen nicht, dass ${\tilde x}$ ein Minimum ist. Beispiel dafür ist die Funktion

$f(x)= \sin (\pi x)+\pi x$ .

Sie ist quasikonvex, da monoton wachsend. Ihre Ableitung verschwindet unendlich oft, aber sie besitzt kein Minimum.

Unter Verwendung der zweiten Ableitung

Ist die Funktion zweimal differenzierbar und quasikonvex, so gilt für alle $x \in D$ und $y\in {\mathbb {R}}^{n}$ , dass aus $y^{T}\nabla f(x)=0$ folgt, dass $y^{T}\nabla ^{2}f(x)y\geq 0$ . Im Falle einer Funktion auf $\mathbb {R}$ vereinfacht sich dies zu $f'(x)=0\implies f''(x)\geq 0$

Darstellung durch Familien von konvexen Funktionen

In der Anwendung ist man oftmals interessiert, Niveaumengen von quasikonvexen Funktionen durch eine Familie von konvexen Funktionen zu modellieren. Dieser Fall taucht beispielsweise bei Optimierungsproblemen mit quasikonvexen Restriktionsfunktionen auf. Die Niveaumengen sind zwar konvex, aber konvexe Funktionen sind einfacher zu Handhaben als quasikonvexe. Gesucht wird also eine Familie von konvexen Funktionen $\psi_t$ für $t\in \mathbb{R}$ , so dass

$f(x) \leq t \iff \psi_t(x)\leq 0$

für eine quasikonvexe Funktion gilt. Die quasikonvexe Restriktion

$f(x)-t \leq 0$

lässt sich dann durch die konvexe Restriktion

$\psi_t(x) \leq 0$

ersetzen. Das quasikonvexe Optimierungsproblem ist dann ein konvexes Optimierungsproblem. $\psi_t(x)$ ist immer eine monoton wachsende Funktion in , es gilt also $t_1 \leq t_2 \implies \psi_{t_1}(x) \leq \psi_{t_2}(x)$ .

Eine Darstellung der Niveaumengen existiert immer, zum Beispiel durch die erweiterte Funktion

$\psi_t (x)= \begin{cases}0 & \text{ falls } f(x) \leq t \\ + \infty & \text{ sonst } \end{cases}$ .

Sie ist aber nicht eindeutig. Meist ist man an differenzierbaren Funktionen, die die Niveaumengen beschreiben interessiert.

Anwendungen in der Wirtschaftstheorie

In der Theorie des Haushaltsoptimums treten quasikonkave Nutzenfunktionen auf.
In der Theorie des Nash-Gleichgewichtes betrachtet man quasikonkave Auszahlungsfunktionen.

Basierend auf einem Artikel in:

Wikipedia.de