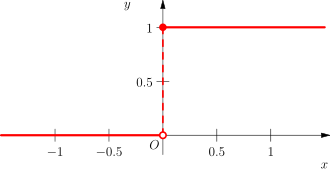
Unstetigkeitsstelle
In der Analysis, einem Teilgebiet der Mathematik, wird eine Funktion innerhalb ihres Definitionsbereichs überall dort als unstetig bezeichnet, wo sie nicht stetig ist. Eine Stelle, an der eine Funktion unstetig ist, bezeichnet man daher auch als Unstetigkeitsstelle oder Unstetigkeit.
Im Artikel Stetigkeit wird erklärt, wann eine Funktion stetig ist und wann sie unstetig ist. In diesem Artikel werden verschiedene Sorten (Klassen) von Unstetigkeiten dargestellt. Dabei werden nur reellwertige Funktionen auf einem reellen Intervall betrachtet.
Definition
Wie erwähnt, heißt eine auf dem reellen Intervall
definierte Funktion
unstetig an der Stelle
,
falls sie dort nicht stetig ist. Man spricht auch von einer auf einer Menge
unstetigen Funktion, wenn die Funktion an jeder Stelle
unstetig ist.
Klassifizierungen von Unstetigkeitsstellen
Es werden verschiedene „Sorten“ von Unstetigkeitsstellen unterschieden. Dazu werden die einseitigen Grenzwerte betrachtet:
Für ein reelles Intervall
und
betrachte man an der Stelle
den linksseitigen Grenzwert
und den rechtsseitigen Grenzwert
Nun ist
genau dann stetig in
,
falls beide Grenzwerte existieren und gleich dem Funktionswert an der Stelle
sind:
.
Andernfalls ist
an der Stelle unstetig. Folgende Fälle sind dabei möglich:
- Eine Unstetigkeitsstelle heißt hebbar, falls die Grenzwerte
und
existieren, endlich sind und gleich sind. Solch eine Unstetigkeit lässt sich entfernen, genauer: Die Funktion
ist an der Stellestetig.
- Falls beide Grenzwerte existieren und endlich, aber ungleich sind, spricht
man von einer Sprungstelle und definiert den Sprung
. Für hebbare Unstetigkeiten lässt sich der Sprung natürlich auch definieren, er ist dann
. Existieren auf dem gesamten Definitionsbereich einer Funktion alle einseitigen Grenzwerte und sind diese endlich, heißt die Funktion sprungstetig oder Regelfunktion.
- Einen Pol (oder Polstelle) nennt man eine Unstetigkeit, an
der
und
existieren, jedoch einer oder beide Grenzwerte nur im uneigentlichen Sinne, d.h., sie nehmen die Werte
oder
an (siehe auch Polstelle).
- Schließlich gibt es noch die Möglichkeit, dass wenigstens einer der Grenzwerte weder eigentlich noch uneigentlich existiert.
Die Fälle 1. und 2. werden auch als Unstetigkeitsstellen erster Art bezeichnet; Die Fälle 3. und 4. entsprechend als Unstetigkeiten zweiter Art, oder manchmal auch als wesentliche Unstetigkeiten.
Darstellung von Unstetigkeitsstellen in Funktionsgraphen
Existieren für die Unstetigkeitsstelle ein links- und/oder rechtsseitiger Grenzwert, werden diese im Graphen der Funktion als kleine Kreise dargestellt, die, falls der betreffende Grenzwert gleichzeitig Funktionswert an der betreffenden Stelle ist, ausgefüllt werden, andernfalls dagegen leer bleiben (oder in vereinfachten Darstellungen mitunter auch gänzlich weggelassen werden).
Beispiele
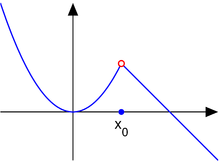
Beispiel 1: Die Funktion
hat an der Stelle
eine hebbare Unstetigkeit.

Beispiel 2: Die Funktion
hat an der Stelle
eine Sprungstelle mit einem Sprung von 1.
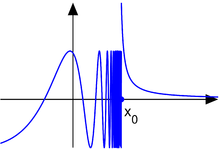
Beispiel 3: Die Funktion
hat an der Stelle
eine Unstetigkeit zweiter Art. Der linksseitige Grenzwert existiert nicht (weder
eigentlich noch uneigentlich), der rechtsseitige Grenzwert ist
.
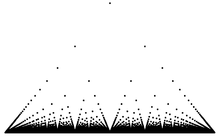
Beispiel 4: Die Thomaesche Funktion ist auf den rationalen Zahlen unstetig und auf den irrationalen Zahlen stetig. Die Dirichlet-Funktion ist auf ihrem gesamten Definitionsbereich unstetig.
Unstetigkeiten monotoner Funktionen
Ist die Funktion
auf dem reellen Intervall
monoton,
so existieren für alle
die einseitigen Grenzwerte
und
.
Daher haben solche monotonen Funktionen keine Unstetigkeitsstellen dritter Art.
Die Menge der Unstetigkeitsstellen erster Art von solchen monotonen Funktionen
ist höchstens abzählbar,
kann aber durchaus dicht
im Definitionsbereich liegen.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 01.02. 2021