
Vorzeichenfunktion
Die Vorzeichenfunktion oder Signumfunktion (von lateinisch signum Zeichen) ist in der Mathematik eine Funktion, die einer reellen oder komplexen Zahl ihr Vorzeichen zuordnet.
Vorzeichenfunktion auf den reellen Zahlen
Definition

Die reelle Vorzeichenfunktion bildet von der Menge der reellen
Zahlen in die Menge
ab und wird in der Regel wie folgt definiert:
Sie ordnet also den positiven Zahlen den Wert +1, den negativen Zahlen den Wert −1 und der 0 den Wert 0 zu.
Bei Anwendungen in der Rechentechnik verzichtet man mitunter auf eine Sonderstellung der 0, diese wird dann den positiven, negativen oder beiden Zahlenbereichen zugeordnet. Dadurch lässt sich das Vorzeichen einer Zahl in einem einzigen Bit kodieren.
Ableitung und Integral
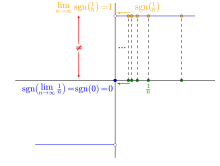
Die Vorzeichenfunktion ist an der Stelle
nicht stetig und damit dort nicht klassisch differenzierbar. Für alle anderen
Stellen
ist die Vorzeichenfunktion differenzierbar mit
.
Die Vorzeichenfunktion besitzt auch keine schwache
Ableitung. Allerdings ist sie im Sinne von Distributionen
differenzierbar, und ihre Ableitung ist
,
wobei
die Delta-Distribution
bezeichnet.
Ferner gilt für alle
Die Vorzeichenfunktion ist darüber hinaus die schwache Ableitung der Betragsfunktion.
Vorzeichenfunktion auf den komplexen Zahlen
Definition
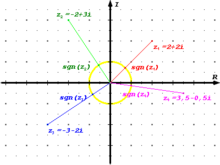
Im Vergleich zur Vorzeichenfunktion reeller Zahlen wird nur selten die folgende Erweiterung auf komplexe Zahlen betrachtet:
Das Ergebnis dieser Funktion liegt für
auf dem Einheitskreis
und besitzt dasselbe Argument wie der Ausgangswert, insbesondere gilt
Beispiel:
(im Bild rot)
Rechenregeln
Für die komplexe Vorzeichenfunktion gelten die folgenden Rechenregeln:
Für alle komplexen Zahlen
und
gilt:
für alle
wobei
den Betrag von
bezeichnet;
, wobei der Querstrich die komplexe Konjugation bezeichnet;
, insbesondere
für positive reelle
,
für negative reelle
,
;
.
- Falls
ist, gilt auch
-
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 05.11. 2017