Komplexe Zahl

$\mathbb {C}$

Der Buchstabe C mit Doppelstrich
steht für die Menge der komplexen Zahlen

Die komplexen Zahlen erweitern den Zahlenbereich der reellen Zahlen derart, dass die Gleichung x^2 + 1 = 0 lösbar wird. Da der Körper der reellen Zahlen ein geordneter Körper ist und damit alle reellen Quadratzahlen nichtnegativ sind, kann die Lösung dieser Gleichung nicht reell sein. Man braucht also eine neue Zahl, sie wird $\mathrm {i}$ genannt, mit der Eigenschaft $\mathrm {i} ^{2}=-1.$ Diese Zahl $\mathrm {i}$ wird als imaginäre Einheit bezeichnet. In der Elektrotechnik wird stattdessen der Buchstabe $\mathrm {j}$ verwendet, um einer Verwechslung mit einer (durch oder i(t) bezeichneten) von der Zeit abhängigen Stromstärke vorzubeugen.

Komplexe Zahlen können in der Form $a+b\cdot \mathrm i$ dargestellt werden, wobei und reelle Zahlen sind und $\mathrm {i}$ die imaginäre Einheit ist. Auf die so dargestellten komplexen Zahlen lassen sich die üblichen Rechenregeln für reelle Zahlen anwenden, wobei $\mathrm i^2$ stets durch ersetzt werden kann und umgekehrt. Für die Menge der komplexen Zahlen wird das Symbol $\mathbb {C}$ (Unicode U+2102: ℂ, siehe Buchstabe mit Doppelstrich) verwendet.

Der so konstruierte Zahlenbereich der komplexen Zahlen bildet einen Erweiterungskörper der reellen Zahlen und hat eine Reihe vorteilhafter Eigenschaften, die sich in vielen Bereichen der Natur- und Ingenieurwissenschaften als äußerst nützlich erwiesen haben. Einer der Gründe für diese positiven Eigenschaften ist die algebraische Abgeschlossenheit der komplexen Zahlen. Dies bedeutet, dass jede algebraische Gleichung positiven Grades über den komplexen Zahlen eine Lösung besitzt, was für reelle Zahlen nicht gilt. Diese Eigenschaft ist der Inhalt des Fundamentalsatzes der Algebra. Ein weiterer Grund ist ein Zusammenhang zwischen trigonometrischen Funktionen und der Exponentialfunktion (Eulerformel), der über die komplexen Zahlen hergestellt werden kann. Ferner ist jede auf einer offenen Menge einmal komplex differenzierbare Funktion dort auch beliebig oft differenzierbar – anders als in der Analysis der reellen Zahlen. Die Eigenschaften von Funktionen mit komplexen Argumenten sind Gegenstand der Funktionentheorie, auch komplexe Analysis genannt.

Definition

Die komplexen Zahlen lassen sich als Zahlbereich im Sinne einer Menge von Zahlen, für die die Grundrechenarten Addition, Multiplikation, Subtraktion und Division erklärt sind, mit den folgenden Eigenschaften definieren:

Die reellen Zahlen sind in den komplexen Zahlen enthalten. Das heißt, dass jede reelle Zahl eine komplexe Zahl ist.
Das Assoziativgesetz und das Kommutativgesetz gelten für die Addition und die Multiplikation komplexer Zahlen.
Das Distributivgesetz gilt.
Für jede komplexe Zahl existiert eine komplexe Zahl , sodass .
Für jede von null verschiedene komplexe Zahl existiert eine komplexe Zahl $\tfrac{1}{x}$ , sodass $x\cdot {\tfrac {1}{x}}=1$ .
Es existiert eine komplexe Zahl $\mathrm {i}$ mit der Eigenschaft $\mathrm i^2=-1$ .
Unter allen Zahlbereichen mit den zuvor genannten Eigenschaften sind die komplexen Zahlen minimal.

Die letzte Forderung ist gleichbedeutend damit, dass sich jede komplexe Zahl in der Form $a+b\cdot\mathrm i$ (bzw. in verkürzter Notation $a+b\,\mathrm i$ oder auch $a+\mathrm {i} \,b$ ) mit reellen Zahlen und darstellen lässt. Die imaginäre Einheit $\mathrm {i}$ ist dabei keine reelle Zahl. Die Existenz eines solchen Zahlbereichs wird im Abschnitt zur Konstruktion der komplexen Zahlen nachgewiesen.

Unter Verwendung der Begriffe Körper und Isomorphie lässt sich das so formulieren: Es gibt minimale Körper, die den Körper der reellen Zahlen und ein Element $\mathrm {i}$ mit der Eigenschaft $\mathrm i^2=-1$ + enthalten. In einem solchen Körper hat jedes Element eine und nur eine Darstellung als $z=a+b\,\mathrm {i}$ mit reellen a, b. Die komplexen Zahlen sind isomorph zu jedem solchen Körper.

Die Koeffizienten a,b werden als Real- bzw. Imaginärteil von $a + b\,\mathrm i$ bezeichnet. Dafür haben sich zwei Notationen etabliert:

$a=\operatorname {Re} {(a+b\,\mathrm {i} )}$ und $b=\operatorname {Im} {(a+b\,\mathrm {i} )}$
$a=\Re {(a+b\,\mathrm {i} )}$ und $b=\Im {(a+b\,\mathrm {i} )}$

Notation

Die Notation in der Form $a+b\,\mathrm i\$ wird auch als (nach René Descartes benannte) kartesische oder algebraische Form bezeichnet. Die Bezeichnung kartesisch erklärt sich aus der Darstellung in der komplexen bzw. gaußschen Zahlenebene (siehe weiter unten). Es findet sich auch die Darstellung $\left( a, b\right)$ ; in der Norm DIN 1302:1999 Allgemeine mathematische Zeichen und Begriffe kommt sie allerdings nicht vor.

In der Elektrotechnik wird das kleine i schon für zeitlich veränderliche Ströme verwendet (siehe Wechselstrom) und kann zu Verwechslungen mit der imaginären Einheit $\mathrm {i}$ führen. Daher kann in diesem Bereich gemäß DIN 1302 der Buchstabe j verwendet werden.

In der Physik wird zwischen für die Stromstärke bei Wechselstrom und $\mathrm {i}$ für die imaginäre Einheit unterschieden. Dies führt durch die recht klare Trennung beim aufmerksamen Leser nicht zu Verwechslungen und wird in dieser Form weitgehend sowohl in der physikalisch-experimentellen als auch in der physikalisch-theoretischen Literatur angewandt; handschriftlich ist diese Feinheit allerdings nicht zu halten, weshalb häufig das $\mathrm {j}$ als Symbol für die imaginäre Einheit verwendet wird. Siehe auch: Komplexe Wechselstromrechnung

Komplexe Zahlen können gemäß DIN 1304-1 und DIN 5483-3 unterstrichen dargestellt werden, um sie von reellen Zahlen zu unterscheiden.

Rechnen in der algebraischen Form

Addition

Die Addition zweier komplexer Zahlen in der komplexen Ebene veranschaulicht

Für die Addition zweier komplexer Zahlen $z_{1}=a+b\,\mathrm {i}$ mit $a,b\in \mathbb {R}$ und $z_{2}=c+d\,\mathrm {i}$ mit $c,d\in {\mathbb {R}}$ gilt

$z_{1}+z_{2}=(a+c)+(b+d)\,\mathrm {i} .$

Subtraktion

Für die Subtraktion zweier komplexer Zahlen $z_{1}$ und $z_{2}$ (siehe Addition) gilt

$z_{1}-z_{2}=(a-c)+(b-d)\,\mathrm {i} .$

Multiplikation

Für die Multiplikation zweier komplexer Zahlen $z_{1}$ und $z_{2}$ (siehe Addition) gilt

$z_{1}\cdot z_{2}=(ac+bd\,\mathrm {i} ^{2})+(ad+bc)\,\mathrm {i} =(ac-bd)+(ad+bc)\,\mathrm {i} .$

Division

Für die Division der komplexen Zahl $z_{1}$ durch die komplexe Zahl $z_{2}$ (siehe Addition) mit $z_{2}\neq 0$ erweitert man den Bruch mit der zum Nenner $z_{2}$ konjugiert komplexen Zahl ${\bar {z}}_{2}=c-d\,\mathrm {i}$ . Der Nenner wird dadurch reell (und ist gerade das Quadrat des Betrages von $c+d\,\mathrm i$ ):

${\frac {z_{1}}{z_{2}}}={\frac {(a+b\,\mathrm {i} )(c-d\,\mathrm {i} )}{(c+d\,\mathrm {i} )(c-d\,\mathrm {i} )}}={\frac {ac+bd}{c^{2}+d^{2}}}+{\frac {bc-ad}{c^{2}+d^{2}}}\mathrm {i} .$

Rechenbeispiele

Addition:

$(3+2\mathrm {i} )+(5+5\mathrm {i} )=(3+5)+(2+5)\mathrm {i} =8+7\mathrm {i}$

Subtraktion:

$(5+5\mathrm i) - (3+2\mathrm i) = (5-3) + (5-2)\mathrm i = 2 + 3\mathrm i$

Multiplikation:

$(3+5\mathrm {i} )\cdot (4+11\mathrm {i} )=(3\cdot 4-5\cdot 11)+(3\cdot 11+5\cdot 4)\mathrm {i} =-43+53\mathrm {i}$

Division:

${{\frac {(2+5{\mathrm {i}})}{(3+7{\mathrm {i}})}}={\frac {(2+5{\mathrm {i}})}{(3+7{\mathrm {i}})}}\cdot {\frac {(3-7{\mathrm {i}})}{(3-7{\mathrm {i}})}}={\frac {(6+35)+(15{\mathrm {i}}-14{\mathrm {i}})}{(9+49)+(21{\mathrm {i}}-21{\mathrm {i}})}}={\frac {41+{\mathrm {i}}}{58}}={\frac {41}{58}}+{\frac {1}{58}}\cdot {\mathrm {i}}}$

Weitere Eigenschaften

Der Körper der komplexen Zahlen ist einerseits ein Oberkörper von , andererseits ein zweidimensionaler $\mathbb {R}$ -Vektorraum. Der Isomorphismus wird auch als natürliche Identifikation bezeichnet. In der Regel nutzt man dies auch, um formell als mit der entsprechenden komplexen Multiplikation zu definieren und dann zu setzen. Dabei wird gleichzeitig festgelegt:
1. Die Drehung der komplexen Ebene am Ursprung um den positiven Winkel $+{\tfrac {\pi }{2}}$ überführt die positive reelle in die positiv-imaginäre Einheit $+{\mathrm {i}}$ .
2. Wenn die positiv-reelle Halbachse in der komplexen Ebene nach rechts geht, dann legt man die positiv-imaginäre Halbachse nach oben. Das ist in Einklang mit dem mathematisch-positiven Drehsinn.
Die Körpererweiterung $\mathbb {C} :\mathbb {R}$ ist vom Grad $[\mathbb {C} :\mathbb {R} ]=2$ ; genauer ist $\mathbb {C}$ isomorph zum Faktorring $\R[X]/(X^2+1)$ , wobei das Minimalpolynom von $\mathrm {i}$ über $\mathbb {R}$ ist. Ferner bildet $\mathbb {C}$ bereits den algebraischen Abschluss von $\mathbb {R}$ .
Als $\mathbb {R}$ -Vektorraum besitzt $\mathbb {C}$ die Basis $\{1, \mathrm{i}\}$ . Daneben ist $\mathbb {C}$ wie jeder Körper auch ein Vektorraum über sich selbst, also ein eindimensionaler $\mathbb {C}$ -Vektorraum mit Basis $\{1\}$ .
$\mathrm {i}$ und $-\mathrm{i}$ sind genau die Lösungen der quadratischen Gleichung . In diesem Sinne kann $\mathrm {i}$ (aber auch $\mathrm {-i}$ ) als „Wurzel aus “ aufgefasst werden.^[1]
$\mathbb {C}$ ist im Gegensatz zu $\mathbb {R}$ kein geordneter Körper, d.h., es gibt keine mit der Körperstruktur verträgliche lineare Ordnungsrelation auf $\mathbb {C}$ . Von zwei unterschiedlichen komplexen Zahlen kann man daher nicht sinnvoll (bezogen auf die Addition und Multiplikation in $\mathbb {C}$ ) festlegen, welche von beiden die größere bzw. die kleinere Zahl ist.

Betrag und Metrik

Betrag

Der Betrag |z| einer komplexen Zahl ist die Länge ihres Vektors in der Gaußschen Zahlenebene und lässt sich z.B. zu

$|z| = \sqrt{a^2 + b^2}$

aus ihrem Realteil $\operatorname{Re}{(z)}=a$ und Imaginärteil $\operatorname{Im}{(z)}=b$ berechnen. Als eine Länge ist der Betrag reell und nicht negativ.

Beispiele:

$|4+3\mathrm {i} |={\sqrt {4^{2}+3^{2}}}={\sqrt {16+9}}={\sqrt {25}}=5$

$|239+\mathrm i| = \sqrt{239^2+1^2} = \sqrt{57121+1} = \sqrt{57122} = 169\cdot\sqrt{2}$

Metrik

Die durch die Abstandsfunktion $d_{\mathbb {C} }(z_{1},z_{2}):=|z_{1}-z_{2}|$ induzierte Metrik versieht den komplexen Vektorraum $\mathbb {C}$ mit seiner Standardtopologie. Sie stimmt mit der Produkttopologie von $\R \times \R$ überein, wie die Einschränkung $d_{\R}$ von $d_{\mathbb {C} }$ auf $\mathbb {R}$ mit der Standardmetrik auf $\mathbb {R}$ übereinstimmt.

Beide Räume $\mathbb {C}$ wie $\mathbb {R}$ sind vollständig unter diesen Metriken. Auf beiden Räumen lässt sich der topologische Begriff der Stetigkeit zu analytischen Begriffen wie Differentiation und Integration erweitern.

Komplexe Zahlenebene

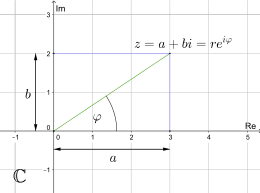
Gaußsche Ebene mit einer komplexen Zahl in kartesischen Koordinaten (a,b) und in Polarkoordinaten (r,φ)

Während sich die Menge $\mathbb {R}$ der reellen Zahlen durch Punkte auf einer Zahlengeraden veranschaulichen lässt, kann man die Menge $\mathbb {C}$ der komplexen Zahlen als Punkte in einer Ebene (komplexe Ebene, gaußsche Zahlenebene) darstellen. Dies entspricht der „doppelten Natur“ von $\mathbb {C}$ als zweidimensionalem reellem Vektorraum. Die Teilmenge der reellen Zahlen bildet darin die waagerechte Achse, die Teilmenge der rein imaginären Zahlen (d.h. mit Realteil 0) bildet die senkrechte Achse. Eine komplexe Zahl $z = a+b\,\mathrm{i}$ mit $a,b \in \R$ besitzt dann die horizontale Koordinate und die vertikale Koordinate , wird also mit dem Zahlenpaar (a,b) identifiziert.

Gemäß Definition entspricht die Addition komplexer Zahlen der Vektoraddition, wobei man die Punkte in der Zahlenebene mit ihren Ortsvektoren identifiziert. Die Multiplikation ist in der gaußschen Ebene eine Drehstreckung, was nach Einführung der Polarform weiter unten klarer werden wird.

Polarform

Die Farbdarstellung der komplexen Zahlenebene wird häufig zur Veranschaulichung komplexer Funktionen (hier: der Identität) angewendet. Die Farbe kodiert das Argument $\arg$ und die Helligkeit gibt den Betrag $|\cdot |$ an.

Verwendet man anstelle der kartesischen Koordinaten $a=\operatorname {Re} (z)$ und $b=\operatorname {Im} (z)$ Polarkoordinaten r = |z| und $\varphi =\arg(z)$ mit $\arg$ als der Argument-Funktion, kann man die komplexe Zahl $z=a+b\,\mathrm{i}$ auch in der folgenden, auf der eulerschen Relation beruhenden sogenannten Polarform (auch Polardarstellung)

$z=r\cdot \mathrm {e} ^{\mathrm {i} \varphi }=r\cdot (\cos \varphi +\mathrm {i} \cdot \sin \varphi )$

darstellen, die sich aus $a = r \cdot \cos \varphi$ und $b = r \cdot \sin \varphi$ ergibt. Die Darstellung mit Hilfe der komplexen e-Funktion $r\cdot \mathrm {e} ^{\mathrm {i} \varphi }$ heißt dabei auch Exponentialdarstellung (der Polarform), die Darstellung mittels des Ausdrucks $r \cdot (\cos \varphi + \mathrm{i} \cdot \sin \varphi)$ trigonometrische Darstellung (der Polarform). Aufgrund der eulerschen Relation sind beide Darstellungen gleichwertig. Des Weiteren gibt es für sie, namentlich in der Praxis, die verkürzten Schreibweisen

$z = r \cdot\operatorname{cis}\,\varphi = r \cdot\operatorname{E}\,(\varphi) = r\,\angle\,\varphi\,,$

in denen $\operatorname{cis}\, \varphi$ für die Summe $\cos \varphi + \mathrm{i} \cdot \sin \varphi$ steht und die Darstellung mit dem Winkeloperator $\angle$ als Versordarstellung bezeichnet wird.

In der komplexen Zahlenebene entspricht dabei der euklidischen Vektorlänge (d.h. dem Abstand zum Ursprung 0) und $\varphi$ dem mit der reellen Achse eingeschlossenen Winkel der Zahl . Üblicherweise jedoch nennt man hier den Betrag von (oder auch seinen Modul) (Schreibweise r = |z| ) und den Winkel $\varphi$ das Argument (oder auch die Phase) von (Schreibweise $\varphi = \operatorname{arg}(z)$ ).

Da $\varphi$ und $\varphi+2\pi$ dabei derselben Zahl zugeordnet werden können, ist die Polardarstellung zunächst nicht eindeutig. Deshalb schränkt man $\varphi$ meist auf das Intervall $(-\pi;\pi]$ , also $-\pi < \varphi \leq \pi$ ein, um anschließend statt vom Argument selbst von seinem Hauptwert für $z\neq 0$ zu sprechen. Der Zahl z=0 indes ließe sich jedes beliebige Argument zuordnen, und zum Zweck einer eindeutigen Darstellung kann man es in diesem Fall tatsächlich auf 0 festlegen.

Das Argument von ist auch der Imaginärteil des komplexen natürlichen Logarithmus

$\ln z=\ln|z|+\mathrm i\cdot\arg (z).$

Mit der Wahl eines auf ganz $\mathbb {C}$ definierten Zweiges des Logarithmus ist also auch eine Argumentfunktion bestimmt (und umgekehrt).

Alle Werte $\mathrm {e} ^{\mathrm {i} \varphi }$ bilden den Einheitskreis der komplexen Zahlen mit dem Betrag , diese Zahlen werden auch unimodular genannt und bilden die Kreisgruppe.

Dass die Multiplikation von komplexen Zahlen (außer der Null) Drehstreckungen entspricht, lässt sich mathematisch wie folgt ausdrücken: Die multiplikative Gruppe $\mathbb {C} ^{\times }$ der komplexen Zahlen ohne die Null lässt sich als direktes Produkt der Gruppe der Drehungen, der Kreisgruppe, und der Streckungen um einen Faktor ungleich Null, der multiplikativen Gruppe $\R^+$ auffassen. Erstere Gruppe lässt sich durch das Argument $\varphi$ parametrisieren, zweitere entspricht gerade den Beträgen.

Komplexe Konjugation

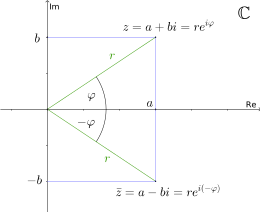
→ Hauptartikel: Konjugation (Mathematik)

Eine komplexe Zahl $z = a+b\,\mathrm{i}$ und die zu ihr konjugiert komplexe Zahl $\bar z=a-b\,\mathrm{i}$

Ändert man das Vorzeichen des Imaginärteils einer komplexen Zahl $z = a+b\,\mathrm{i},$ so erhält man die zu konjugiert komplexe Zahl $\bar z=a-b\,\mathrm{i}$ (manchmal auch z^* geschrieben).

Die Konjugation $\mathbb {C} \to \mathbb {C} ,\,z\mapsto {\bar {z}}$ ist ein (involutorischer) Körperautomorphismus, da sie mit Addition und Multiplikation verträglich ist, d.h., für alle $y,z\in \mathbb {C}$ gilt

$\overline{y+z}=\bar y+\bar z,\quad \overline{y\cdot z}=\bar y\cdot \bar z.$

In der Polardarstellung hat die konjugiert komplexe Zahl ${\bar {z}}$ bei unverändertem Betrag gerade den negativen Winkel von Man kann die Konjugation in der komplexen Zahlenebene also als die Spiegelung an der reellen Achse interpretieren. Insbesondere werden unter der Konjugation genau die reellen Zahlen auf sich selbst abgebildet.

Das Produkt aus einer komplexen Zahl $z=a+b\,\mathrm{i}$ und ihrer komplex Konjugierten ${\bar {z}}$ ergibt das Quadrat ihres Betrages:

$z\cdot {\bar {z}}=(a+b\,\mathrm {i} )(a-b\,\mathrm {i} )=a^{2}+b^{2}=|z|^{2}$

Die komplexen Zahlen bilden damit ein triviales Beispiel einer C*-Algebra.

Die Summe aus einer komplexen Zahl $z=a+b\,\mathrm{i}$ und ihrer komplex Konjugierten ${\bar {z}}$ ergibt das 2-Fache ihres Realteils:

$z+{\bar {z}}=(a+b\,\mathrm {i} )+(a-b\,\mathrm {i} )=2a=2\,\operatorname {Re} {(z)}$

Die Differenz aus einer komplexen Zahl $z=a+b\,\mathrm{i}$ und ihrer komplex Konjugierten ${\bar {z}}$ ergibt das $\mathrm {2i}$ -Fache ihres Imaginärteils:

$z-{\bar {z}}=(a+b\,\mathrm {i} )-(a-b\,\mathrm {i} )=2b\,\mathrm {i} =2\,\mathrm {i} \,\operatorname {Im} {(z)}$

Umrechnungsformeln

Von der algebraischen Form in die Polarform

Für > $z=a+b\,\mathrm{i}$ in algebraischer Form ist

$r = |z| = \sqrt{a^2 + b^2}=\sqrt{z \cdot \overline z}.$

Für $z=0\quad (\Longleftrightarrow r=0)$ ist das Argument $\varphi$ beliebig, wird aber häufig auf 0 gesetzt oder undefiniert gelassen. Für $z \neq 0$ kann das Argument $\varphi$ im Intervall $(-\pi;\pi]$ mit Hilfe einer trigonometrischen Umkehrfunktion, bspw. mit Hilfe des Arkuskosinus

$\varphi =\arg(z)={\Biggl \{}{\begin{matrix}\\\\\end{matrix}}{\Biggr .}$	$\arccos {\frac {a}{r}}$	für $b\geq 0$	${\Biggl .}{\begin{matrix}\\\\\end{matrix}}{\Biggr \}}\;=\operatorname {arctan2} (a,b)$
	$-\arccos {\frac {a}{r}}$	für

ermittelt werden. Verfahren, die den Arkustangens verwenden, sind im Artikel Arkustangens und Arkuskotangens § Umrechnung ebener kartesischer Koordinaten in polare aufgeführt. Dazu gehört auch die in vielen Programmiersprachen und Tabellenkalkulationen zur Verfügung gestellte häufig mit dem Namen arctan2, aber auch atan2, bezeichnete Variante der Arkustangensfunktion, die beide Werte übergeben bekommt und das Ergebnis je nach Vorzeichen von und dem passenden Quadranten zuordnet.

Die Berechnung des Winkels $\varphi$ im Intervall $[0,2\pi)$ kann im Prinzip so durchgeführt werden, dass der Winkel zunächst wie vorstehend beschrieben im Intervall $(-\pi ,\pi ]$ berechnet wird und dann um $2\pi$ vergrößert wird, falls er negativ ist:

$\varphi' = \arg(z) = \begin{cases} \varphi + 2\pi & \text{falls}\ \varphi < 0\\ \varphi & \text{sonst} \end{cases}$

(siehe Polarkoordinaten).

Von der Polarform in die algebraische Form

$a=\operatorname {Re} (z)=r\cdot \cos \varphi$

$b=\operatorname {Im} (z)=r\cdot \sin \varphi$

Wie weiter oben stellt den Realteil und den Imaginärteil jener komplexen Zahl dar.

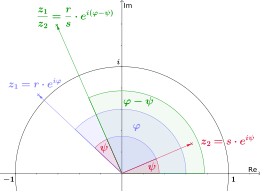
Arithmetische Operationen in der Polarform

Durch arithmetische Operationen sind folgende Operanden miteinander zu verknüpfen:

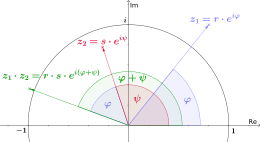
$z_{1}=r_{1}\cdot (\cos \varphi _{1}+\mathrm {i} \cdot \sin \varphi _{1})=r_{1}\cdot \mathrm {e} ^{\mathrm {i} \varphi _{1}}$

$z_{2}=r_{2}\cdot (\cos \varphi _{2}+\mathrm {i} \cdot \sin \varphi _{2})=r_{2}\cdot \mathrm {e} ^{\mathrm {i} \varphi _{2}}$

Bei der Multiplikation werden die Beträge $r_{1}$ und $r_{2}$ miteinander multipliziert und die zugehörigen Phasen $\varphi_1$ bzw. $\varphi_2$ addiert. Bei der Division wird der Betrag des Dividenden durch den Betrag des Divisors geteilt und die Phase des Divisors von der Phase des Dividenden subtrahiert. Für die Addition und die Subtraktion existiert auch eine, etwas kompliziertere, Formel:

Trigonometrische Form

Die Multiplikation von zwei komplexen Zahlen entspricht dem Addieren der Winkel und dem Multiplizieren der Beträge.

${z_{1}\cdot z_{2}=r_{1}\cdot r_{2}\cdot \left[\cos(\varphi _{1}+\varphi _{2})+\mathrm {i} \cdot \sin(\varphi _{1}+\varphi _{2})\right]}$

Die Division von zwei komplexen Zahlen entspricht dem Subtrahieren der Winkel und dem Dividieren der Beträge.

${\frac {z_{1}}{z_{2}}}={\frac {r_{1}}{r_{2}}}\cdot \left[\cos(\varphi _{1}-\varphi _{2})+\mathrm {i} \cdot \sin(\varphi _{1}-\varphi _{2})\right]$

$z_{1}\pm z_{2}=t\cdot (\cos \chi +\mathrm {i} \cdot \sin \chi )$

mit $t:={\sqrt {r_{1}^{2}+r_{2}^{2}\pm 2r_{1}r_{2}\cos(\varphi _{1}-\varphi _{2})}},$
$\chi :=\operatorname {arctan2} \left(r_{1}\cos \varphi _{1}\pm r_{2}\cos \varphi _{2},r_{1}\sin \varphi _{1}\pm r_{2}\sin \varphi _{2}\right)$
und der arctan2-Funktion.

Exponentialform

$z_{1}\cdot z_{2}=r_{1}\cdot r_{2}\cdot \mathrm {e} ^{\mathrm {i} (\varphi _{1}+\varphi _{2})}$
${\frac {z_{1}}{z_{2}}}={\frac {r_{1}}{r_{2}}}\cdot \mathrm {e} ^{\mathrm {i} (\varphi _{1}-\varphi _{2})}$
$z_{1}\pm z_{2}=t\cdot \mathrm {e} ^{\mathrm {i} \chi }$ mit und $\chi$ wie oben.

Rechenoperationen 3. Stufe

Zu den Rechenoperationen der dritten Stufe gehören Potenzieren, Wurzelziehen (Radizieren) und Logarithmieren.

Potenzen

Natürliche Exponenten

Für natürliche Zahlen berechnet sich die -te Potenz in der polaren Form $z=r\mathrm {e} ^{\mathrm {i} \varphi }$ zu

$z^{n}=r^{n}\cdot \mathrm {e} ^{\mathrm {i} n\varphi }=r^{n}\cdot (\cos n\varphi +\mathrm {i} \cdot \sin n\varphi )$

(siehe den Satz von de Moivre) oder für die algebraische Form $z=a+b\,\mathrm {i}$ mit Hilfe des binomischen Satzes zu

$z^{n}=\sum _{k=0, \atop k{\text{ gerade}}}^{n}{\binom {n}{k}}(-1)^{\frac {k}{2}}a^{n-k}b^{k}+\mathrm {i} \sum _{k=1, \atop k{\text{ ungerade}}}^{n}{\binom {n}{k}}(-1)^{\frac {k-1}{2}}a^{n-k}b^{k}.$

Beliebige komplexe Exponenten

Die allgemeine Definition einer Potenz mit komplexer Basis $z\neq 0$ und komplexem Exponenten $\omega$ lautet

$z^{\omega }:=\mathrm {e} ^{\omega \cdot \ln z},$

wobei $\ln(z)$ für den Hauptwert des komplexen Logarithmus steht (siehe unten), damit liefert die Formel ebenfalls einen Hauptwert. Im Fall $\omega \in \mathbb{Z}$ allerdings stimmen alle in Frage kommenden Ergebnisse mit diesem Hauptwert überein und die Funktion wird eindeutig.

Wurzeln

→ Hauptartikel: Wurzeln aus komplexen Zahlen

Logarithmen

Der komplexe natürliche Logarithmus ist (anders als der reelle auf $\mathbb {R} ^{+}$ ) nicht eindeutig. Eine komplexe Zahl heißt Logarithmus der komplexen Zahl , wenn

$\mathrm {e} ^{w}=z.$

Mit ist auch jede Zahl $w+2\pi \mathrm {i} k$ mit beliebigem $k\in \mathbb {Z}$ ein Logarithmus von . Man arbeitet daher mit Hauptwerten, d.h. mit Werten eines bestimmten Streifens der komplexen Ebene.

Der Hauptwert des natürlichen Logarithmus der komplexen Zahl

$z=r\mathrm {e} ^{\mathrm {i} \varphi }\in \mathbb {C} ^{\times }$

ist

$\ln z=\ln r+\mathrm {i} \varphi$

mit r>0 und $-\pi <\varphi \leq \pi$ . Anders formuliert: Der Hauptwert des natürlichen Logarithmus der komplexen Zahl $z\in \mathbb {C} ^{\times }$ ist

$\ln z=\ln |z|+\mathrm {i} \,\arg(z),$

wobei $\arg(z)$ der Hauptwert des Arguments von ist.

Naheliegenderweise gelten die Logarithmengesetze für den Hauptwert des natürlichen Logarithmus nur modulo $2\pi \mathrm {i} \mathbb {Z}$ .

Die endlichen Untergruppen

Genau die Zahlen $\mathrm {e} ^{\mathrm {i} \varphi }$ bilden den Einheitskreis der komplexen Zahlen mit dem Betrag $1$ , diese Zahlen werden auch unimodular genannt und bilden die Kreisgruppe.

Alle Elemente einer endlichen Untergruppe der multiplikativen Einheitengruppe $\mathbb {C} ^{\times }=\mathbb {C} \setminus \{0\}$ sind Einheitswurzeln. Unter allen Ordnungen von Gruppenelementen gibt es eine maximale, etwa $n\in \mathbb {N}$ . Da $\mathbb {C}$ kommutativ ist, erzeugt ein Element mit dieser maximalen Ordnung dann auch die Gruppe, so dass die Gruppe zyklisch ist und genau aus den Elementen

$\exp \left({2\pi \mathrm {i} k \over n}\right),\quad k=0,1,\dotsc ,n-1$

besteht. Alle Elemente liegen auf dem Einheitskreis.

Die Vereinigung aller endlichen Untergruppen ist eine Gruppe, die zur Torsionsgruppe $\Q/\Z$ isomorph ist. Sie liegt dicht in ihrer Vervollständigung, der schon erwähnten Kreisgruppe, die auch als 1-Sphäre aufgefasst werden kann und zu $\mathbb{R} /\mathbb{Z }$ isomorph ist.

Pragmatische Rechenregeln

Am einfachsten lassen sich die Berechnungen folgendermaßen durchführen:

Addition und Subtraktion komplexer Zahlen werden (in der algebraischen Form) komponentenweise durchgeführt.
Die Multiplikation komplexer Zahlen kann je nach Vorgabe vorteilhaft in algebraischer Form oder in Exponentialform (Multiplikation der Beträge und Addition der Argumente (Winkel)) durchgeführt werden.
Bei der Division komplexer Zahlen werden in Exponentialform ihre Beträge dividiert und ihre Argumente (Winkel) subtrahiert, oder in algebraischer Form der Quotient mit dem konjugierten Nenner erweitert.
Beim Potenzieren einer komplexen Zahl mit einem reellen Exponenten wird ihr Betrag potenziert und ihr Argument (Winkel) mit dem Exponenten multipliziert; die Benutzung der algebraischen Form (mit Newtons Binomialsatz) ist in den meisten Fällen umständlicher (insbesondere für höhere Potenzen).
Beim Radizieren (Wurzelziehen) einer komplexen Zahl mit einem reellen Exponenten wird ihr Betrag radiziert und ihr Argument (Winkel) durch den Exponenten dividiert. Hierdurch entsteht die erste Lösung. Bei einer -ten Wurzel entstehen Lösungen, die im Winkel von $2\pi/n$ um den Ursprung der gaußschen Ebene verteilt sind. Siehe Wurzel (Mathematik). Eine Quadratwurzel kann auch recht einfach in kartesischer Form berechnet werden.
Beim Multiplizieren in algebraischer Form lässt sich durch folgendes Verfahren eine der vier Multiplikation einsparen. Allerdings sind drei zusätzliche Additionen bzw. Subtraktionen notwendig und die Berechnung lässt sich schlechter parallelisieren.

$p_{1}=(a-b)(c+d)$

$p_{2}=bc$

$p_{3}=ad$

$\operatorname {Re} (z_{1}z_{2})=p_{1}+p_{2}-p_{3}$

$\operatorname {Im} (z_{1}z_{2})=p_{2}+p_{3}$

Konstruktion der komplexen Zahlen

In diesem Abschnitt wird nachgewiesen, dass tatsächlich ein Körper $\mathbb {C}$ der komplexen Zahlen existiert, der den in der obigen Definition geforderten Eigenschaften genügt. Es sind dabei verschiedene Konstruktionen möglich, die jedoch bis auf Isomorphie zum selben Körper führen.

Paare reeller Zahlen

Die Konstruktion nimmt zunächst keinerlei Bezug auf die imaginäre Einheit $\mathrm {i}$ : Im 2-dimensionalen reellen Vektorraum $\mathbb {R} ^{2}$ der geordneten reellen Zahlenpaare z=(a,b) wird neben der Addition

$(a,b)+(c,d):=(a+c,b+d)$

(das ist die gewöhnliche Vektoraddition) eine Multiplikation durch

$(a,b)\cdot (c,d):=(a\cdot c-b\cdot d,a\cdot d+b\cdot c)$

definiert.

Nach dieser Festlegung schreibt man $\mathbb {C} =\mathbb {R} ^{2}$ , und $(\mathbb {C} ,+,\cdot )$ wird zu einem Körper, dem Körper der komplexen Zahlen. Die imaginäre Einheit wird dann durch $\mathrm {i} :=(0,1)$ definiert.

Da $\{(1,0),(0,1)\}=\{1,\mathrm {i} \}$ eine Basis des $\mathbb {R} ^{2}$ bilden, lässt sich damit als Linearkombination

$z=1\cdot (a,0)+\mathrm {i} \cdot (b,0)=a+\mathrm {i} b$

darstellen.

Erste Eigenschaften

Die Abbildung $\mathbb {R} \to \mathbb {C} ,\,a\mapsto (a,0)$ ist eine Körpereinbettung von $\mathbb {R}$ in $\mathbb {C}$ , aufgrund derer wir die reelle Zahl mit der komplexen Zahl identifizieren.

Bezüglich der Addition ist:

die Zahl das neutrale Element (das Nullelement) in $\mathbb {C}$ und
die Zahl das inverse Element in $\mathbb {C}$ .

Bezüglich der Multiplikation ist:

die Zahl das neutrale Element (das Einselement) von $\mathbb {C}$ und
das Inverse (Reziproke) zu $z=(a,b)\neq (0,0)$ ist $z^{-1} = \left(\frac{a}{a^2+b^2},\,\frac{-b}{a^2+b^2}\right)$ .

Bezug zur Darstellung in der Form a + bi

Durch $\mathrm i:=(0,1)$ wird die imaginäre Einheit festgelegt; für diese gilt $\mathrm {i} ^{2}=(0,1)^{2}=(-1,0)$ , was nach obiger Einbettung gleich $-1\in \mathbb{R}$ entspricht.

Jede komplexe Zahl $z=(a,b)\in \mathbb {C}$ besitzt die eindeutige Darstellung der Form

$z = (a,b) = (a,0)+(0,b)=a\cdot(1,0)+b\cdot(0,1) = a + b\,\mathrm{i}$

mit $a,b\in\R$ ; dies ist die übliche Schreibweise für die komplexen Zahlen.

Polynome: Adjunktion

Eine weitere Konstruktion der komplexen Zahlen ist der Faktorring

$\R[X]/(X^2+1)$

des Polynomringes in einer Unbestimmten über den reellen Zahlen. Die Zahl $\mathrm {i}$ entspricht dabei dem Bild der Unbestimmten , die reellen Zahlen werden mit den konstanten Polynomen identifiziert.

Dieses Konstruktionsprinzip ist auch in anderem Kontext anwendbar, man spricht von Adjunktion.

Matrizen

Die Menge der $2\times 2$ -Matrizen der Form

$Z = \begin{pmatrix}a&-b\\b&a\end{pmatrix} = a \begin{pmatrix}1&0\\0&1\end{pmatrix} + b \begin{pmatrix}0&-1\\1&0\end{pmatrix} = a \cdot E + b \cdot I$ mit $a,b\in\R$

bildet ebenfalls ein Modell der komplexen Zahlen. Dabei werden die reelle Einheit bzw. die imaginäre Einheit $\mathrm {i}$ durch die Einheitsmatrix bzw. die Matrix dargestellt. Daher gilt:

$\operatorname {Re}(Z)=a$

$\operatorname {Im}(Z)=b$

$\operatorname{abs}(Z) = \sqrt{a^2 + b^2} = \sqrt{\det Z}$

Diese Menge ist ein Unterraum des Vektorraums der reellen $2\times 2$ -Matrizen.

Reelle Zahlen entsprechen Diagonalmatrizen $\begin{pmatrix}a&0\\0&a\end{pmatrix}.$

Die zu den Matrizen gehörenden linearen Abbildungen sind, sofern und nicht beide null sind, Drehstreckungen im Raum $\mathbb {R} ^{2}$ . Es handelt sich um genau dieselben Drehstreckungen wie bei der Interpretation der Multiplikation mit einer komplexen Zahl $a+b\mathrm i$ in der gaußschen Zahlenebene.

Geschichte

Der Begriff „komplexe Zahlen“ wurde von Carl Friedrich Gauß (Theoria residuorum biquadraticorum, 1831) eingeführt, der Ursprung der Theorie der komplexen Zahlen geht auf die italienischen Mathematiker Gerolamo Cardano (Ars magna, Nürnberg 1545) und Rafael Bombelli (L’Algebra, Bologna 1572; wahrscheinlich zwischen 1557 und 1560 geschrieben) zurück.

Die Unmöglichkeit eines naiven Radizierens der Art $x^{2}=-1\Rightarrow x=\pm {\sqrt {-1}}$ ist bei der Behandlung quadratischer Gleichungen schon sehr früh bemerkt und hervorgehoben worden, z.B. schon in der um 820 n.Chr. verfassten Algebra des Muhammed ibn Mûsâ Alchwârizmî. Aber bei dem nächstliegenden und unanfechtbaren Schluss, dass diese Art von Gleichung nicht lösbar sei, blieb die mathematische Forschung nicht stehen.

In gewissem Sinne ist bereits der Italiener Gerolamo Cardano (1501–1576) in seinem 1545 erschienenen Buch Artis magnae sive de regulis algebraicis liber unus darüber hinausgegangen. Er behandelt dort die Aufgabe, zwei Zahlen zu finden, deren Produkt 40 und deren Summe 10 ist. Er hebt hervor, dass die dafür anzusetzende Gleichung

keine Lösung hat, fügt aber einige Bemerkungen hinzu, indem er in die Lösung

$x_{1,2}=-{\frac {p}{2}}\pm {\sqrt {{\frac {p^{2}}{4}}-q}}$

der allgemeinen normierten quadratischen Gleichung

$x^{2}+px+q=0$

für und die Werte −10 bzw. 40 einsetzt. Wenn es also möglich wäre, dem sich ergebenden Ausdruck

${\sqrt {25-40}}={\sqrt {-15}}$

einen Sinn zu geben, und zwar so, dass man mit diesem Zeichen nach denselben Regeln rechnen dürfte wie mit einer reellen Zahl, so würden die Ausdrücke

$5 + \sqrt{-15}$

$5 - \sqrt{-15}$

in der Tat je eine Lösung darstellen.

Für die Quadratwurzel aus negativen Zahlen und allgemeiner für alle aus einer beliebigen reellen Zahl $\alpha$ und einer positiven reellen Zahl $\beta$ zusammengesetzten Zahlen

$\alpha + \sqrt{-\beta}$ oder $\alpha - \sqrt{-\beta}$

hat sich seit der Mitte des 17. Jahrhunderts die Bezeichnung imaginäre Zahl eingebürgert, die ursprünglich von René Descartes stammt, der in seiner La Géométrie (1637) damit die Schwierigkeit des Verständnisses komplexer Zahlen als nichtreeller Lösungen algebraischer Gleichungen ausdrückte. John Wallis erzielte im 17. Jahrhundert erste Fortschritte in Hinblick auf eine geometrische Interpretation komplexer Zahlen. Gottfried Wilhelm Leibniz nannte sie 1702 eine feine und wunderbare Zuflucht des menschlichen Geistes, beinahe ein Zwitterwesen zwischen Sein und Nichtsein. Die Einführung der imaginären Einheit $\mathrm {i}$ als neue Zahl wird Leonhard Euler zugeschrieben. Er erzielte durch Rechnen mit imaginären Zahlen wertvolle neue Erkenntnisse, zum Beispiel veröffentlichte er die Eulersche Formel 1748 in seiner Einführung in die Analysis und veröffentlichte erstmals explizit die Formel von Abraham de Moivre (Ende des 17. Jahrhunderts, dieser wiederum hatte sie von Isaac Newton), aber auch Euler hatte noch große Schwierigkeiten beim Verständnis und der Einordnung komplexer Zahlen, obwohl er routinemäßig damit rechnete.

Die geometrische Interpretation wurde zuerst vom dänischen Landvermesser Caspar Wessel (1799 veröffentlicht in den Abhandlungen der Königlich Dänischen Akademie der Wissenschaften, aber erst rund hundert Jahre später weiteren Kreisen bekannt), von Jean-Robert Argand (in einem obskuren Privatdruck 1806, den aber Legendre zur Kenntnis kam und der 1813 breiteren Kreisen bekannt wurde) und Gauß (unveröffentlicht) entdeckt. Gauß erwähnt die Darstellung explizit in einem Brief an Friedrich Bessel vom 18. Dezember 1811. Nach Argand wird die geometrische Darstellung in der Zahlenebene manchmal auch Arganddiagramm genannt.

Als Begründer der komplexen Analysis gilt Augustin-Louis Cauchy in einer 1814 bei der französischen Akademie eingereichten Arbeit über Integration im Komplexen, die aber erst 1825 veröffentlicht wurde. 1821 definierte er in seinem Lehrbuch Cours d’analyse eine Funktion einer komplexen Variablen in die komplexe Zahlenebene und bewies viele grundlegende Sätze der Funktionentheorie.

Ausgehend von philosophischen Ideen Immanuel Kants fand William Rowan Hamilton 1833 eine logisch einwandfreie Begründung der komplexen Zahlen als geordnetes Paar reeller Zahlen. Er deutete die komplexe Zahl $a+b\cdot\mathrm i$ als Zahlenpaar (a,b) und definierte Addition beziehungsweise die Multiplikation durch:

${\begin{aligned}(a_{1},b_{1})+(a_{2},b_{2})&=(a_{1}+a_{2},b_{1}+b_{2})\\(a_{1},b_{1})(a_{2},b_{2})&=(a_{1}a_{2}-b_{1}b_{2},a_{1}b_{2}+a_{2}b_{1})\end{aligned}}$

Heute machen diese Dinge keinerlei begriffliche oder tatsächliche Schwierigkeiten. Durch die Einfachheit der Definition, der bereits erläuterten Bedeutung und Anwendungen in vielen Wissenschaftsgebieten stehen die komplexen Zahlen den reellen Zahlen in nichts nach. Der Begriff der „imaginären“ Zahlen, im Sinne von eingebildeten bzw. unwirklichen Zahlen, hat sich also im Laufe der Jahrhunderte zu einer schiefen, aber beibehaltenen Bezeichnung entwickelt.

Bedeutung

Komplexe Zahlen in der Physik

Komplexe Zahlen spielen in der Grundlagenphysik eine zentrale Rolle. In der Quantenmechanik wird der Zustand eines physikalischen Systems als Element eines (projektiven) Hilbertraums über den komplexen Zahlen aufgefasst. Komplexe Zahlen finden Verwendung bei der Definition von Differentialoperatoren in der Schrödingergleichung und der Klein-Gordon-Gleichung. Für die Dirac-Gleichung benötigt man eine Zahlbereichserweiterung der komplexen Zahlen, die Quaternionen. Alternativ ist eine Formulierung mit Pauli-Matrizen möglich, die aber die gleiche algebraische Struktur wie die Quaternionen aufweisen.

Komplexe Zahlen haben in der Physik und Technik eine wichtige Rolle als Rechenhilfe. So lässt sich insbesondere die Behandlung von Differentialgleichungen zu Schwingungsvorgängen vereinfachen, da sich damit die komplizierten Beziehungen in Zusammenhang mit Produkten von Sinus- bzw. Kosinusfunktionen durch Produkte von Exponentialfunktionen ersetzen lassen, wobei lediglich die Exponenten addiert werden müssen. So fügt man dazu beispielsweise in der komplexen Wechselstromrechnung geeignete Imaginärteile in die reellen Ausgangsgleichungen ein, die man bei der Auswertung der Rechenergebnisse dann wieder ignoriert. Dadurch werden in der Zwischenrechnung harmonische Schwingungen (reell) zu Kreisbewegungen in der komplexen Ebene ergänzt, die mehr Symmetrie aufweisen und deswegen einfacher zu behandeln sind.

In der Optik werden die brechenden und absorbierenden Effekte einer Substanz in einer komplexen, wellenlängenabhängigen Permittivität (Dielektrizitätskonstante) oder dem komplexen Brechungsindex zusammengefasst, die wiederum auf die elektrische Suszeptibilität zurückgeführt wird.

In der Fluiddynamik werden komplexe Zahlen eingesetzt, um ebene Potentialströmungen zu erklären und zu verstehen. Jede beliebige komplexe Funktion eines komplexen Arguments stellt immer eine ebene Potentialströmung dar – der geometrische Ort entspricht dem komplexen Argument in der gaußschen Zahlenebene, das Strömungspotenzial dem Realteil der Funktion, und die Stromlinien den Isolinien des Imaginärteils der Funktion mit umgekehrtem Vorzeichen. Das Vektorfeld der Strömungsgeschwindigkeit entspricht der konjugiert komplexen ersten Ableitung der Funktion. Durch das Experimentieren mit verschiedenen Überlagerungen von Parallelströmung, Quellen, Senken, Dipolen und Wirbeln kann man die Umströmung unterschiedlicher Konturen darstellen. Verzerren lassen sich diese Strömungsbilder durch konforme Abbildung – das komplexe Argument wird durch eine Funktion des komplexen Arguments ersetzt. Beispielsweise lässt sich die Umströmung eines Kreiszylinders (Parallelströmung + Dipol) in die Umströmung eines tragflügel-ähnlichen Profils (Joukowski-Profil) verzerren und die Rolle des tragenden Wirbels an einer Flugzeug-Tragfläche studieren. So nützlich diese Methode zum Lernen und Verstehen ist, zur genauen Berechnung reicht sie im Allgemeinen nicht aus.

Komplexe Zahlen in der Elektrotechnik

In der Elektrotechnik besitzt die Darstellung elektrischer Größen mit Hilfe komplexer Zahlen weite Verbreitung. Sie wird bei der Berechnung von zeitlich sinusförmig veränderlichen Größen wie elektrischen und magnetischen Feldern verwendet. Bei der Darstellung einer sinusförmigen Wechselspannung als komplexe Größe und entsprechenden Darstellungen für Widerstände, Kondensatoren und Spulen vereinfachen sich die Berechnungen des elektrischen Stromes, der Wirk- und der Blindleistung in einer Schaltung. Die durch Differentialquotienten oder Integrale gegebene Verkopplung geht über in eine Verkopplung durch trigonometrische Funktionen; die Berechnung der Zusammenhänge lässt sich damit wesentlich erleichtern. Auch das Zusammenwirken mehrerer verschiedener sinusförmiger Spannungen und Ströme, die zu unterschiedlichen Zeitpunkten ihre Nulldurchgänge haben können, lässt sich in komplexer Rechnung leicht darstellen. Genaueres über dieses Thema steht im Artikel über die komplexe Wechselstromrechnung.

In den letzten Jahren hat die digitale Signalverarbeitung außerordentlich an Bedeutung gewonnen, deren Fundament die Rechnung mit komplexen Zahlen bildet.

Körpertheorie und algebraische Geometrie

Der Körper der komplexen Zahlen ist der algebraische Abschluss des Körpers der reellen Zahlen.

Je zwei algebraisch abgeschlossene Körper mit derselben Charakteristik und demselben Transzendenzgrad über ihrem Primkörper (der durch die Charakteristik festgelegt ist) sind (ringtheoretisch) isomorph. Bei einem Körper von Charakteristik 0 mit überabzählbarem Transzendenzgrad ist dieser gleich der Kardinalität des Körpers. Körpertheoretisch bilden die komplexen Zahlen also den einzigen algebraisch abgeschlossenen Körper mit Charakteristik 0 und der Kardinalität $\aleph$ des Kontinuums. Eine Konstruktion des Körpers der komplexen Zahlen ist mithilfe dieser Feststellung auch rein algebraisch etwa als Erweiterung des algebraischen Abschlusses der rationalen Zahlen um $\aleph$ viele transzendente Elemente möglich. Eine weitere Konstruktion liefert ein Ultraprodukt: Hierzu bilde man zu jedem endlichen Körper seinen algebraischen Abschluss und bilde von ihnen das Ultraprodukt bezüglich eines beliebigen freien Ultrafilters. Aus dem Satz von Łoś folgt, dass dieses Ultraprodukt ein algebraisch abgeschlossener Körper mit Charakteristik 0 ist, die Kardinalität des Kontinuums folgt aus mengentheoretischen Überlegungen.

Unter dem Schlagwort Lefschetz-Prinzip werden verschiedene Sätze zusammengefasst, die es erlauben, Ergebnisse der algebraischen Geometrie, die über den komplexen Zahlen bewiesen werden, auf andere algebraisch abgeschlossene Körper mit Charakteristik 0 zu übertragen (was maßgeblich auf der Vollständigkeit der Theorie der algebraisch abgeschlossenen Körper mit Charakteristik 0 aufbaut). Die Betrachtung des komplexen Falls bietet den Vorteil, dass dort topologische und analytische Methoden eingesetzt werden können, um algebraische Ergebnisse zu erhalten. Obige Ultraproduktkonstruktion erlaubt die Übertragung von Ergebnissen im Fall einer Charakteristik ungleich 0 auf die komplexen Zahlen.

Spektraltheorie und Funktionalanalysis

Viele Ergebnisse der Spektraltheorie gelten für komplexe Vektorräume in größerem Umfang als für reelle. So treten z.B. komplexe Zahlen als Eigenwerte reeller Matrizen auf (dann jeweils zusammen mit dem konjugiert-komplexen Eigenwert). Das erklärt sich dadurch, dass das charakteristische Polynom der Matrix aufgrund der algebraischen Abgeschlossenheit von $\mathbb {C}$ über den komplexen Zahlen stets in Linearfaktoren zerfällt. Dagegen gibt es reelle Matrizen ohne reelle Eigenwerte, während das Spektrum eines beliebigen beschränkten Operators auf einem komplexen (mindestens eindimensionalen) Banachraum nie leer ist. In der Spektraltheorie auf Hilberträumen lassen sich Sätze, die im reellen Fall nur für selbstadjungierte Operatoren gelten, im komplexen Fall oft auf normale Operatoren übertragen.

Auch in weiteren Teilen der Funktionalanalysis spielen die komplexen Zahlen eine besondere Rolle. So wird etwa die Theorie der C*-Algebren meist im Komplexen betrieben, die harmonische Analyse befasst sich mit Darstellungen von Gruppen auf komplexen Hilberträumen.

Funktionentheorie und komplexe Geometrie

Das Studium differenzierbarer Funktionen auf Teilmengen der komplexen Zahlen ist Gegenstand der Funktionentheorie. Sie ist in vieler Hinsicht starrer als die reelle Analysis und lässt weniger Pathologien zu. Beispiele sind die Aussage, dass jede in einem Gebiet differenzierbare Funktion bereits beliebig oft differenzierbar ist, oder der Identitätssatz für holomorphe Funktionen.

Die Funktionentheorie ermöglicht oft auch Rückschlüsse auf rein reelle Aussagen, beispielsweise lassen sich manche Integrale mit dem Residuensatz berechnen. Ein wichtiges Einsatzgebiet dieser Methoden ist die analytische Zahlentheorie, die Aussagen über ganze Zahlen auf Aussagen über komplexe Funktionen zurückführt, häufig in der Form von Dirichletreihen. Ein prominentes Beispiel ist die Verbindung zwischen Primzahlsatz und riemannscher ζ-Funktion. In diesem Zusammenhang spielt die riemannsche Vermutung eine zentrale Rolle.

Die oben erwähnte Starrheit holomorpher Funktionen tritt noch stärker bei globalen Fragen in Erscheinung, d.h. beim Studium komplexer Mannigfaltigkeiten. So gibt es auf einer kompakten komplexen Mannigfaltigkeit keine nichtkonstanten globalen holomorphen Funktionen; Aussagen wie der Einbettungssatz von Whitney sind im Komplexen also falsch. Diese sogenannte „analytische Geometrie“ (nicht mit der klassischen analytischen Geometrie von René Descartes zu verwechseln!) ist auch eng mit der algebraischen Geometrie verknüpft, viele Ergebnisse lassen sich übertragen. Die komplexen Zahlen sind auch in einem geeigneten Sinne ausreichend groß, um die Komplexität algebraischer Varietäten über beliebigen Körpern der Charakteristik 0 zu erfassen (Lefschetz-Prinzip).

Literatur

Reinhold Remmert: Komplexe Zahlen. In D. Ebbinghaus u.a. (Hrsg.): Zahlen. Springer, 1983.

Anmerkungen

↑ Bei Verwendung des Zeichens $\mathrm {i}$ ist noch deutlicher gemacht, als es vielleicht bei Verwendung von $\sqrt{-1}$ wäre, dass bei jedem Vorkommen dieselbe Lösung von $\mathrm {i} ^{2}+1=0$ (dasselbe „Vorzeichen“) genommen werden muss. Dennoch bleiben alle algebraischen Aussagen gültig, wenn überall $\mathrm {i}$ durch $-\mathrm{i}$ ersetzt wird.

Basierend auf einem Artikel in:

Wikipedia.de