Antisymmetrische Relation

Eine antisymmetrische Relation, als gerichteter Graph dargestellt

Eine nicht antisymmetrische Relation, als gerichteter Graph dargestellt

Antisymmetrisch heißt eine zweistellige Relation auf einer Menge, wenn für beliebige Elemente und der Menge mit xRy nicht zugleich die Umkehrung yRx gelten kann, es sei denn, und sind gleich. Äquivalent formuliert gilt damit für beliebige Elemente und dieser Menge, dass aus xRy und yRx stets x=y folgt.

Die Antisymmetrie ist eine der Voraussetzungen für eine Halbordnung.

Definition

Ist eine Menge und $R\subseteq M\times M$ eine zweistellige Relation auf , dann heißt antisymmetrisch, wenn (unter Verwendung der Infixnotation) gilt:

$\forall x,y\in M:xRy\land yRx\Rightarrow x=y$

Sonderfall Asymmetrische Relation

Jede asymmetrische Relation ist auch eine antisymmetrische Relation. Da für eine asymmetrische Relation auf

$\forall x,y\in M:xRy\Rightarrow \neg (yRx)$ gilt, also für keines der geordneten Paare (x,y)

die Umkehrung zutrifft,

ist die Prämisse $xRy\land yRx$ der Definition der antisymmetrischen Relation stets falsch und nach dem logischen Prinzip Ex falso quodlibet somit die Aussage $\forall x,y\in M:xRy\land yRx\Rightarrow x=y$ erfüllt.

Die Asymmetrie ist eine der Voraussetzungen für eine (irreflexive) Striktordnung.

Beispiele

Antisymmetrisch sind die Relationen $\leq$ und $\geq$ auf den reellen Zahlen. Aus $x\leq y$ und $y \le x$ folgt x=y . Das Gleiche gilt für $x\geq y$ und $y\geq x$ .

Auch die Teilbarkeitsrelation $\mid$ für natürliche Zahlen ist antisymmetrisch, denn aus $a\mid b$ und $b\mid a$ folgt a=b . Die Teilbarkeit auf den ganzen Zahlen ist hingegen nicht antisymmetrisch, weil beispielsweise $3\mid -3$ und $-3\mid 3$ gilt, obwohl $-3\neq 3$ .

Asymmetrische Relationen sind die Kleiner-Relation auf den reellen Zahlen und die Teilmengenbeziehung $\subset$ zwischen Mengen. Verglichen mit $\leq$ beziehungsweise $\subseteq$ fehlt diesen Beziehungen die Reflexivität.

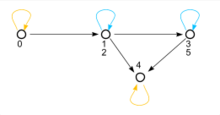
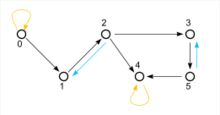
Darstellung als gerichteter Graph

Jede beliebige Relation auf einer Menge kann als gerichteter Graph aufgefasst werden (Beispiel siehe oben). Die Knoten des Graphen sind dabei die Elemente von . Vom Knoten zum Knoten wird genau dann eine gerichtete Kante (ein Pfeil $a\longrightarrow b$ ) gezogen, wenn $a\,R\,b$ gilt.

Die Antisymmetrie von lässt sich im Graphen nun so charakterisieren: Wann immer es einen Pfeil $a\longrightarrow b$ zwischen verschiedenen Knoten und des Graphen gibt, dann kann es nicht gleichzeitig einen Pfeil $b\longrightarrow a$ geben.

Schleifen ${\stackrel {a}\circlearrowright }$ brauchen bei diesem Kriterium nicht untersucht zu werden.

Eigenschaften

Mit Hilfe der konversen Relation $R^{-1}$ lässt sich die Antisymmetrie auch durch die folgende Bedingung charakterisieren:

$R\cap R^{{-1}}\subseteq {\mathrm {Id}}_{M}$

Hierbei bezeichnet ${\mathrm {Id}}_{M}$ die identische Relation auf der Grundmenge , also die Menge aller Paare (x,x)

Sind die Relationen und antisymmetrisch, dann gilt dies auch für ihre Schnittmenge $R\cap S$ . Diese Aussage lässt sich von zwei Relationen auf den Durchschnitt $\cap _{{i\in I}}R_{i}$ einer beliebigen (nichtleeren) Familie von antisymmetrischen Relationen verallgemeinern.
Jede Teilmenge einer antisymmetrischen Relation ist wieder antisymmetrisch.

Basierend auf einem Artikel in:

Wikipedia.de