Mehrdimensionale Normalverteilung
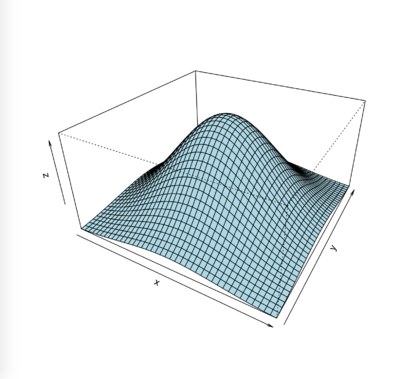
Die mehrdimensionale oder multivariate Normalverteilung ist ein Typ multivariater Wahrscheinlichkeitsverteilungen und stellt eine Verallgemeinerung der (eindimensionalen) Normalverteilung auf mehrere Dimensionen dar.[1] Eine zweidimensionale Normalverteilung wird auch bivariate Normalverteilung genannt.
Bestimmt wird eine multivariate Normalverteilung durch zwei
Verteilungsparameter – den Vektor der Erwartungswerte der eindimensionalen
Komponenten
und durch die Kovarianzmatrix
,
welche den Parametern
und
der eindimensionalen Normalverteilungen entsprechen.
Multivariat normalverteilte Zufallsvariablen treten als Grenzwerte bestimmter Summen unabhängiger mehrdimensionaler Zufallsvariablen auf. Dies ist die Verallgemeinerung des zentralen Grenzwertsatz zum mehrdimensionalen zentralen Grenzwertsatz.
Weil sie entsprechend dort auftreten, wo mehrdimensionale zufällige Größen als Überlagerung vieler voneinander unabhängiger Einzeleffekte angesehen werden können, haben sie für die Praxis eine große Bedeutung.
Aufgrund der sogenannten Reproduktionseigenschaft der multivariaten Normalverteilung lässt sich die Verteilung von Summen (und Linearkombinationen) multivariat normalverteiler Zufallsvariabler konkret angeben, was auf dem Gebiet der multivariaten Statistik eine Rolle spielt.
Die multivariate Normalverteilung: allgemeiner Fall
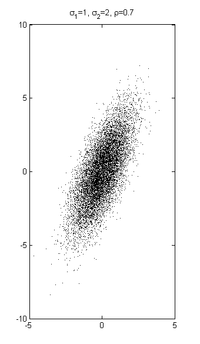
Eine -dimensionale
reelle Zufallsvariable
ist normalverteilt mit Erwartungswertvektor
und (positiv definiter) Kovarianzmatrix
,
wenn sie eine Dichtefunktion
der Form
besitzt. Man schreibt
Für die zugehörige Verteilungsfunktion
gibt es keine geschlossene Formel. Die entsprechenden Integrale müssen numerisch
berechnet werden.
Der Wert im Exponentialteil der Dichtefunktion
entspricht der Mahalanobis-Distanz,
welche die Distanz vom Testpunkt
zum Mittelwert
darstellt. Im Vergleich mit der Dichtefunktion der eindimensionalen
Normalverteilung spielt bei der multivariaten Normalverteilung
die Rolle von
.
Die multivariate Normalverteilung hat die folgenden Eigenschaften:
- Sind die Komponenten von X paarweise unkorreliert, so sind sie auch stochastisch unabhängig.
- Die affine
Transformation
mit einer Matrix
(mit
) und
ist
-dimensional normalverteilt:
. Dies gilt aber nach der hier gegebenen Definition nur, wenn
nicht-singulär ist, also eine nicht-verschwindende Determinante hat.
- Die affine Transformation
-
- standardisiert
den Zufallsvektor
: es ist
(mit Einheitsmatrix
).
kann auch eine singuläre Kovarianzmatrix besitzen. Man spricht dann von einer degenerierten oder singulären multivariaten Normalverteilung. In diesem Fall existiert keine Dichtefunktion.
- Bedingte Verteilung bei partieller Kenntnis des Zufallsvektors: Bedingt man einen multivariat normal verteilten Zufallsvektor auf einen Teilvektor, so ist das Ergebnis selbst wieder multivariat normal verteilt, für
-
- gilt
,
- insbesondere hängt der Erwartungswert linear vom Wert von
ab und die Varianz ist unabhängig vom Wert von
.
Die Randverteilung der multivariaten Normalverteilung
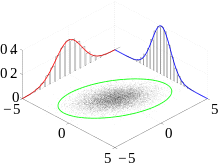
Sei
multivariat normalverteilt. Für eine beliebige Partition
mit
und
,
,
gilt, dass die Randverteilungen
und
(multivariate) Normalverteilungen sind.
Die Umkehrung gilt allerdings nicht, wie folgendes Beispiel zeigt:
Sei
und sei
definiert durch
wobei .
Dann ist ebenso
und
Demnach ist die Kovarianz (und damit die Korrelation) von
und
gleich
genau dann, wenn
.
Aber
und
sind nach Definition nicht unabhängig, da
immer gleich
ist. Daher ist insbesondere
nicht multivariat normalverteilt.
Die p-dimensionale Standardnormalverteilung
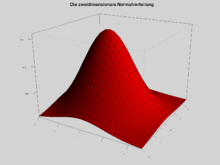
Das Wahrscheinlichkeitsmaß auf ,
das durch die Dichtefunktion
definiert wird, heißt Standardnormalverteilung der Dimension .
Die
-dimensionale
Standardnormalverteilung ist abgesehen von Translationen (d.h.
Erwartungswert
)
die einzige multivariate Verteilung, deren Komponenten stochastisch unabhängig
sind und deren Dichte zugleich rotationssymmetrisch
ist.
Momente und Kumulanten
Wie im univariaten Fall, sind alle Momente der
multivariate Normalverteilung durch die ersten beiden Momente definiert. Alle Kumulanten
außer den ersten beiden sind 0. Die ersten beiden Kumulanten sind dabei der
Mittelwert
und die Kovarianz
.
In Bezug auf das multivariate Momentenproblem
hat die Normalverteilung die Eigenschaft, dass sie durch ihre Momente eindeutig
definiert ist. Das heißt, wenn alle Momente einer multivariaten
Wahrscheinlichkeitsverteilung existieren und den Momenten einer multivariaten
Normalverteilung entsprechen, ist die Verteilung die eindeutige multivariate
Normalverteilung mit diesen Momenten.
Dichte der zweidimensionalen Normalverteilung
Die Dichtefunktion der zweidimensionalen Normalverteilung mit Mittelwert =
(0,0),
und Korrelationskoeffizient
ist
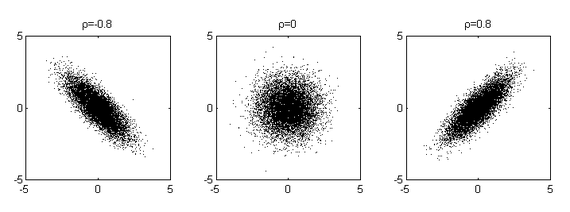
Im allgemeineren zweidimensionalen Fall mit Mittelwert = (0,0) und beliebigen Varianzen ist die Dichtefunktion
und den allgemeinsten Fall mit Mittelwert =
bekommt man durch Translation (ersetze
durch
und
durch
).
Beispiel für eine multivariate Normalverteilung
Betrachtet wird eine Apfelbaumplantage mit sehr vielen gleich alten, also vergleichbaren Apfelbäumen. Man interessiert sich für die Merkmale Größe der Apfelbäume, die Zahl der Blätter und die Erträge. Es werden also die Zufallsvariablen definiert:
:
Höhe eines Baumes [m];
:
Ertrag [100 kg];
:
Zahl der Blätter [1000 Stück].
Die Variablen sind jeweils normalverteilt wie
Die meisten Bäume sind also um 4 ± 1m groß, sehr kleine oder sehr große Bäume
sind eher selten. Bei einem großen Baum ist der Ertrag tendenziell größer als
bei einem kleinen Baum, aber es gibt natürlich hin und wieder einen großen Baum
mit wenig Ertrag. Ertrag und Größe sind korreliert, die Kovarianz beträgt
und der Korrelationskoeffizient
.
Ebenso ist
mit dem Korrelationskoeffizienten
,
und
mit dem Korrelationskoeffizienten
.
Fasst man die drei Zufallsvariablen im Zufallsvektor
zusammen, ist
multivariat normalverteilt. Dies gilt allerdings nicht im Allgemeinen (vgl. Die
Randverteilung der multivariaten Normalverteilung). Im vorliegenden Fall
gilt dann für die gemeinsame
Verteilung von
und
Die entsprechende Korrelationsmatrix ist
Stichproben bei multivariaten Verteilungen
In der Realität werden in aller Regel die Verteilungsparameter einer multivariaten Verteilung nicht bekannt sein. Diese Parameter müssen also geschätzt werden.
Man zieht eine Stichprobe vom Umfang .
Jede Realisation
des Zufallsvektors
könnte man als Punkt in einem
-dimensionalen
Hyperraum auffassen. Man erhält so die
-Datenmatrix
als
, wobei
die in jeder Zeile die Koordinaten eines Punktes enthält.
Der Erwartungswertvektor wird geschätzt durch den Mittelwertvektor der
arithmetischen
Mitteln der Spalten von
mit den Komponenten
Für die Schätzung der Kovarianzmatrix erweist sich die bezüglich der
arithmetischen Mittelwerte zentrierte Datenmatrix
als nützlich. Sie berechnet sich als
mit den Elementen ,
wobei
den Einsvektor,
einen Spaltenvektor der Länge
mit lauter Einsen, darstellt. Es wird also bei allen Einträgen das arithmetische
Mittel der zugehörigen Spalte subtrahiert.
Die -Kovarianzmatrix
hat die geschätzten Komponenten
Sie ergibt sich als
Die Korrelationsmatrix
wird geschätzt durch die paarweisen Korrelationskoeffizienten
auf ihrer Hauptdiagonalen stehen Einsen.
Beispiel zu Stichproben
Es wurden 10 Apfelbäume zufällig ausgewählt und jeweils 3 Eigenschaften
gemessen: :
Höhe eines Baumes [m];
:
Ertrag [100 kg];
:
Zahl der Blätter [1000 Stück]. Diese 10 Beobachtungen werden in der Datenmatrix
zusammengefasst:
Die Mittelwerte berechnen sich, wie beispielhaft an
gezeigt, als
Sie ergeben den Mittelwertvektor
Für die zentrierte Datenmatrix
erhält man die zentrierten Beobachtungen, indem von den Spalten der
entsprechende Mittelwert abzogen wird:
also
Man berechnet für die Kovarianzmatrix die Kovarianzen, wie im Beispiel,
und entsprechend die Varianzen
so dass sich die Kovarianzmatrix
ergibt.
Entsprechend erhält man für die Korrelationsmatrix zum Beispiel
bzw. insgesamt
Erzeugung mehrdimensionaler, normalverteilter Zufallszahlen
Eine oft verwendete Methode zur Erzeugung eines Zufallsvektors
einer
-dimensionalen
Normalverteilung mit Mittelwertvektor
und (symmetrischer
und positiv
definiter) Kovarianzmatrix
kann wie folgt angegeben werden:
- Bestimme eine Matrix
, so dass
. Dazu kann die Cholesky-Zerlegung von
oder eine Quadratwurzel von
verwendet werden.
- Sei
ein Vektor, dessen
Komponenten stochastisch unabhängige, standardnormalverteilte Zufallszahlen sind. Diese können beispielsweise mit Hilfe der Box-Muller-Methode generiert werden.
- Mit der affinen
Transformation
ergibt sich die gewünschte IMG class="text" style="width: 2.07ex; height: 2.17ex; vertical-align: -0.33ex;" alt="N" src="/svg/f5e3890c981ae85503089652feb48b191b57aae3.svg">-dimensionale Normalverteilung.
Streuregionen der mehrdimensionalen Normalverteilung
Für eindimensionale normalverteilte Zufallsvariablen liegen ungefähr
68,27 % der Realisierungen im Intervall ,
für mehrdimensionale normalverteilte Zufallsvariablen sind die Regionen
konstanter Wahrscheinlichkeit durch Ellipsen
(die Standardabweichungsellipsen) gegeben, welche um den Mittelwert zentriert
sind. Die Hauptachsen der Ellipse sind durch die Eigenvektoren der
Kovarianzmatrix
gegeben, die Länge der Halbachsen ist die Quadratwurzel des zur jeweiligen
Hauptachse gehörenden Eigenwertes
.
Eine Realisierung der Zufallsvariablen in der Region anzutreffen, welche durch
die (mehrdimensionale) Standardabweichungsellipse begrenzt wird, ist für eine
mehrdimensional normalverteilte Zufallsvariable weniger wahrscheinlich.

Nach einer Hauptachsentransformation können die Achsen mit ihren jeweiligen
normiert werden. Dann lässt sich die Wahrscheinlichkeit als Funktion von dem
Radius
berechnen, mit der ein Messwert innerhalb dieses Radius liegt. Mit
ist der Anteil
der Messwerte höchstens im Abstand
vom Mittelwert einer p-dimensionalen Normalverteilung. Dabei ist
die regularisierte unvollständige
Gammafunktion der oberen Grenze.
| |
|
| |
| 68,27 | 95,45 | 99,73 | |
| 39,35 | 86,47 | 98,89 | |
| 19,87 | 73,85 | 97,07 |
Entsprechend kann mit der Umkehrfunktion der Streuradius r angegeben werden, in der ein vorgegebener Anteil an Messwerten liegt:
| 0,675 | 1,645 | 2,576 | |
| 1,177 | 2,146 | 3,035 | |
| 1,538 | 2,500 | 3,368 |
Anmerkungen
- ↑ Mehrdimensionale und multivariate Normalverteilung werden in diesem Artikel synonym verwendet. Bei Hartung/Elpelt: Multivariate Statistik haben sie aber (in Kapitel 1, Abschnitt 5) unterschiedliche Bedeutungen: hier ist die multivariate Normalverteilung eine Matrix-Verteilung.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 04.03. 2020