Schätzfunktion

Eine Schätzfunktion, auch Schätzstatistik oder kurz Schätzer, dient in der mathematischen Statistik dazu, aufgrund von vorhandenen empirischen Daten einer Stichprobe einen Schätzwert zu ermitteln und dadurch Informationen über unbekannte Parameter einer Grundgesamtheit zu erhalten. Schätzfunktionen sind die Basis zur Berechnung von Punktschätzungen und zur Bestimmung von Konfidenzintervallen mittels Bereichsschätzern und werden als Teststatistiken in Hypothesentests verwendet. Sie sind spezielle Stichprobenfunktionen und können durch Schätzverfahren, z.B. die Kleinste-Quadrate-Schätzung, die Maximum-Likelihood-Schätzung oder die Momentenmethode, bestimmt werden.

Im Rahmen der Entscheidungstheorie können Schätzfunktionen auch als Entscheidungsfunktionen bei Entscheidungen unter Unsicherheit betrachtet werden.

Formale Definition

Es sei

$T_{n}=h(X_{1:n})$ ,

eine reellwertige Statistik basierend auf einer Zufallsstichprobe $X_{1:n}$ aus einer Verteilung mit Wahrscheinlichkeitsdichtefunktion $f(x;\theta)$ , wobei $\theta$ ein unbekannter skalarer Parameter ist. Wenn die Zufallsvariable $T_{n}$ berechnet wird, um statistische Inferenz bzgl. $\theta$ durchzuführen, spricht man von einem Schätzer. Falls die Stichprobengröße nicht relevant ist, schreibt man auch statt $T_{n}$ . Der konkrete Wert $t=h(x_{1:n})$ , den ein Schätzer für eine Realisierung $x_{1:n}$ der Zufallsstichprobe $X_{1:n}$ annimmt, wird als Schätzung bezeichnet.

Grundkonzepte: Stichprobenvariablen und -funktionen

In der Regel befindet sich der Experimentierende in der Situation, dass er anhand endlich vieler Beobachtungen (einer Stichprobe) Aussagen über die zugrunde liegende Verteilung oder deren Parameter in der Grundgesamtheit treffen möchte.

Nur in seltenen Fällen lässt sich die Grundgesamtheit vollständig erheben (Total- oder Vollerhebung), sodass sie dann exakt die gewünschten Informationen liefert. Ein Beispiel für eine Vollerhebung ist die Arbeitslosenstatistik der amtlichen Statistik.

In den meisten Fällen kann jedoch die Grundgesamtheit nicht vollständig erhoben werden, z.B. weil sie zu groß ist. Interessiert man sich etwa für die mittlere Größe der 18-Jährigen in der EU, müsste man alle 18-Jährigen messen, was praktisch undurchführbar ist. Stattdessen wird nur eine Stichprobe, eine zufällige Auswahl von Elementen, erhoben (Teilerhebung).

Stichprobenvariable

An dieser Stelle setzt die statistische Modellierung an. Die Stichprobenvariable $X_{i}$ , eine Zufallsvariable, beschreibt mit ihrer Verteilung die Wahrscheinlichkeit, mit der eine bestimmte Merkmalsausprägung bei der -ten Ziehung aus der Grundgesamtheit auftritt. Jeder Beobachtungswert $x_{i}$ ist die Realisierung einer Stichprobenvariable $X_{i}$ .

Stichprobenfunktion

→ Hauptartikel: Stichprobenfunktion

Die Definition von Stichprobenvariablen $X_{i}$ erlaubt die Definition von Stichprobenfunktionen analog z.B. zu Kennwerten aus der deskriptiven Statistik:

Arithmetisches Mittel	Stichprobenfunktion
${\overline {x}}:={\frac {1}{n}}(x_{1}+x_{2}+\ldots +x_{n})$	${\overline {X}}:={\frac {1}{n}}(X_{1}+X_{2}+\ldots +X_{n})$

Da jede Stichprobe aufgrund der Zufälligkeit anders ausfällt, sind auch diese Stichprobenfunktionen Zufallsvariablen, deren Verteilung von

der Art der Ziehung der Stichprobe aus der Grundgesamtheit und
der Verteilung des Merkmals in der Grundgesamtheit

abhängt.

Stichprobenverteilung

Unter Stichprobenverteilung versteht man die Verteilung einer Stichprobenfunktion $g(X_{1},\dotsc ,X_{n})$ über alle möglichen Stichproben aus der Grundgesamtheit. Die Stichprobenfunktion ist in der Regel eine Schätzfunktion für einen unbekannten Parameter der Grundgesamtheit oder eine Teststatistik für eine Hypothese über einen unbekannten Parameter der Grundgesamtheit. Daher spricht man statt von Stichprobenverteilung auch einfach von der Verteilung einer Schätzfunktion oder Teststatistik. Die Verteilung der Stichprobenfunktion dient der Gewinnung von Aussagen über unbekannte Parameter in der Grundgesamtheit aufgrund einer Stichprobe.

Die Stichprobenverteilung ist ein frequentistisches Konzept, das bayessche Pendant ist die A-posteriori-Verteilung.

Berechnung der Stichprobenverteilung

Die Stichprobenverteilung für eine Stichprobenfunktion mit bestimmtem Stichprobenumfang aus einer endlichen Grundgesamtheit lässt sich stets berechnen (siehe die folgenden Beispiele), im Allgemeinen jedoch ist man eher an generellen Formeln mit z.B. unbestimmtem Stichprobenumfang interessiert. Wichtige Hilfsmittel sind dabei folgende Aussagen:

Reproduktivität der Normalverteilung: Sind die Stichprobenvariablen $X_{i}$ voneinander unabhängig und normalverteilt ( $X_{i}\sim {\mathcal {N}}(\mu ;\sigma ^{2})$ ), dann ist auch ${\overline {X}}=(X_{1}+\dotsb +X_{n})/n$ normalverteilt ( ${\overline {X}}\sim {\mathcal {N}}(\mu ;\sigma ^{2}/n)$ ).
Zentraler Grenzwertsatz: Sind die Stichprobenvariablen $\ X_{i}$ voneinander unabhängig und existieren für sie die Erwartungswerte $\ \operatorname {E} (X_{i})=\mu$ und $\ \operatorname {E} ((X_{i}-\mu )^{2}{\bigr )}=\operatorname {Var} (X_{i})=\sigma ^{2}$ , ist ${\overline {X}}=(X_{1}+\dotsb +X_{n})/n$ für großes approximativ normalverteilt ( ${\overline {X}}\approx {\mathcal {N}}\left(\mu ;\sigma ^{2}/n\right)$ ).

Bootstrap-Stichprobenverteilungen

Wenn eine hinreichend große Stichprobe repräsentativ für die Grundgesamtheit ist, kann die Stichprobenverteilung für eine beliebige Stichprobenfunktion nichtparametrisch mit Hilfe des Bootstrap-Verfahrens geschätzt werden, ohne dass die Verteilung der $X_{i}$ bekannt sein muss. Jedoch muss allgemein mathematisch gezeigt werden, dass die Bootstrap-Stichprobenverteilungen mit steigender Zahl der Bootstrap-Stichproben gegen die wahre Stichprobenverteilung konvergiert.

Beispiele

Beispiel 1

Gegeben sei eine Urne mit sieben Kugeln mit den Aufschriften 10, 11, 11, 12, 12, 12 und 16. Wenn man zwei Kugeln mit Zurücklegen zieht, zeigt die folgende Tabelle alle möglichen Stichproben aus der Grundgesamtheit:

	10	11	11	12	12	12	16
10	10;10	10;11	10;11	10;12	10;12	10;12	10;16
11	11;10	11;11	11;11	11;12	11;12	11;12	11;16
11	11;10	11;11	11;11	11;12	11;12	11;12	11;16
12	12;10	12;11	12;11	12;12	12;12	12;12	12;16
12	12;10	12;11	12;11	12;12	12;12	12;12	12;16
12	12;10	12;11	12;11	12;12	12;12	12;12	12;16
16	16;10	16;11	16;11	16;12	16;12	16;12	16;16

Jede der möglichen Stichproben tritt mit der Wahrscheinlichkeit von 1/49 auf. Berechnet man nun den Stichprobenmittelwert ${\overline {X}}=(X_{1}+X_{2})/2$ aus den zwei Kugeln, so ergibt sich:

$\overline {X}$	10	11	11	12	12	12	16
10	10,0	10,5	10,5	11,0	11,0	11,0	13,0
11	10,5	11,0	11,0	11,5	11,5	11,5	13,5
11	10,5	11,0	11,0	11,5	11,5	11,5	13,5
12	11,0	11,5	11,5	12,0	12,0	12,0	14,0
12	11,0	11,5	11,5	12,0	12,0	12,0	14,0
12	11,0	11,5	11,5	12,0	12,0	12,0	14,0
16	13,0	13,5	13,5	14,0	14,0	14,0	16,0

Fasst man die Ergebnisse von $\overline {X}$ entsprechend der Wahrscheinlichkeit des Auftretens der Stichprobe zusammen, so erhält man die Stichprobenverteilung von $\overline {X}$ :

	10,0	10,5	11,0	11,5	12,0	13,0	13,5	14,0	16,0
$P({\overline {X}}=x)$	1/49	4/49	10/49	12/49	9/49	2/49	4/49	6/49	1/49

Ändert man die Art der Ziehung, von einer Ziehung mit Zurücklegen in eine Ziehung ohne Zurücklegen, so ergibt sich eine andere Verteilung für $\overline {X}$ . In den oberen Tabellen fällt dann die Hauptdiagonale weg, sodass es nur mögliche Stichproben gibt. Daher ergibt sich dann folgende Verteilung für $\overline {X}$ :

	10,0	10,5	11,0	11,5	12,0	13,0	13,5	14,0	16,0
$P({\overline {X}}=x)$	0	4/42	8/42	12/42	6/42	2/42	4/42	6/42	0

Beispiel 2

In einer Urne sind fünf rote und vier blaue Kugeln. Es werden drei Kugeln ohne Zurücklegen aus dieser Urne gezogen. Definiert man die Stichprobenfunktion : Zahl der roten Kugeln unter den drei gezogenen, ist hypergeometrisch verteilt mit M=5 als Zahl der roten Kugeln in der Urne, N=9 als Gesamtzahl der Kugeln in der Urne und n=3 als Zahl der Versuche. Hier können alle Informationen über die Verteilung von gewonnen werden, weil sowohl das stochastische Modell (Ziehen aus einer Urne) als auch die zugehörigen Parameter (Anzahl der roten und blauen Kugeln) bekannt sind.

Beispiel 3

Ein Lebensmittelgroßmarkt bekommt eine Lieferung von 2000 Gläsern mit Pflaumenkompott. Problematisch sind in den Früchten verbliebene Kerne. Der Kunde toleriert einen Anteil von Gläsern mit Kernen von 5 %. Er möchte sich bei dieser Lieferung vergewissern, dass diese Quote nicht überschritten wird. Eine komplette Erhebung der Grundgesamtheit von 2000 Gläsern ist allerdings nicht durchführbar, denn 2000 Gläser zu kontrollieren ist zu aufwendig und außerdem zerstört das Öffnen eines Glases die Ware.

Allerdings könnte man eine kleine Zahl von Gläsern zufällig aussuchen, also eine Stichprobe nehmen, und die Zahl der zu beanstandenden Gläser zählen. Übersteigt diese Zahl eine bestimmte Grenze, den kritischen Wert der Prüfgröße, geht man davon aus, dass auch in der Lieferung zu viele zu beanstandende Gläser sind.

Eine mögliche Stichprobenfunktion ist $\pi ={\frac {1}{n}}(X_{1}+X_{2}+\ldots +X_{n})$ , wobei $X_{i}$ eine Zufallsvariable bezeichnet, die nur die Werte 1 (Glas enthält Pflaumen mit Kern) oder 0 (Glas enthält keine Pflaumen mit Kern) annimmt.

Wenn die Zufallsvariablen $X_{i}$ Bernoulli-verteilt sind, dann ist aufgrund des zentralen Grenzwertsatzes $\pi$ approximativ normalverteilt.

Schätzfunktionen

Grundgedanke und Konzept der Schätzfunktion

Schätzfunktionen sind spezielle Stichprobenfunktionen, um Parameter oder Verteilungen der Grundgesamtheit zu bestimmen. Beeinflusst werden Schätzfunktionen unter anderem durch

die Art der Ziehung der Stichprobe (z.B. Ziehen mit oder ohne Zurücklegen) und
die Art der Schätzmethode (z.B. Methode der kleinsten Quadrate, Maximum-Likelihood-Methode oder Momentenmethode).

Man möchte letztlich versuchen, ausschließlich anhand des Wissens um das zu Grunde liegende Modell und die beobachtete Stichprobe etwa Intervalle anzugeben, die mit größter Wahrscheinlichkeit den wahren Parameter enthalten. Alternativ möchte man auch bei einer bestimmten Fehlerwahrscheinlichkeit testen, ob eine spezielle Vermutung über den Parameter (zum Beispiel, dass zu viele Gläser Kerne enthalten) bestätigt werden kann. Schätzfunktionen bilden in diesem Sinne die Basis für jede begründete Entscheidung über die Ausprägungen der Grundgesamtheit, die bestmögliche Wahl solcher Funktionen ist das Ergebnis der mathematischen Untersuchung.

Trifft man auf dieser Basis eine Entscheidung, z.B. geht die Lieferung zurück, besteht die Möglichkeit, dass die Entscheidung falsch ist. Es gibt folgende Fehlerquellen:

Die Stichprobe ist nicht repräsentativ für die Grundgesamtheit, d.h., sie spiegelt die Grundgesamtheit nicht wider.
Das Modell für die Zufallsvariablen $X_{i}$ ist falsch.
Die Stichprobe könnte untypisch ausgefallen sein, so dass man die Lieferung fälschlicherweise ablehnt.

Dennoch besteht in der Praxis zumeist keine Alternative zu statistischen Verfahren dieser Art. Den zuvor genannten Problemen tritt man auf verschiedene Weisen entgegen:

Man versucht möglichst eine einfache Zufallsstichprobe zu ziehen.
Die Modelle für die Zufallsvariablen $X_{i}$ werden zum einen möglichst groß gewählt (so dass das "richtige" Modell enthalten ist) und zum anderen wird die Schätzfunktion so gewählt, dass ihre Verteilung für viele Modelle berechenbar ist (siehe Zentraler Grenzwertsatz).
Aufgrund der Schätzfunktion wird eine Irrtumswahrscheinlichkeit angegeben.

Formale Definition der Schätzfunktion

Grundlage einer jeden Schätzfunktion sind die Beobachtungen $x_{i}$ eines statistischen Merkmals . Modelltheoretisch wird dieses Merkmal idealisiert: Man geht davon aus, dass es sich bei den Beobachtungen in Wahrheit um Realisierungen von Zufallsvariablen $X_{i}$ handelt, deren „wahre“ Verteilung und „wahre“ Verteilungsparameter unbekannt sind.

Um Informationen über die tatsächlichen Eigenschaften des Merkmals zu erhalten, erhebt man eine Stichprobe von Elementen. Mit Hilfe dieser Stichprobenelemente schätzt man dann die gesuchten Parameter bzw. die gesuchte Verteilung.

Um also beispielsweise einen Parameter $\gamma$ einer unbekannten Verteilung zu schätzen, hat man es formal mit einer Zufallsstichprobe vom Umfang zu tun, es werden also Realisierungen $x_{i}$ ( $i=1,\dotsc ,n$ ) der Zufallsvariablen $X_{i}$ beobachtet. Die Zufallsvariablen $X_{i}$ werden dann mittels einer Schätzmethode in einer geeigneten Schätzfunktion $g(X_{1},X_{2},\dotsc ,X_{n})$ zusammengefasst. Formal wird dabei vorausgesetzt, dass eine messbare Funktion ist.

Zur Vereinfachung der Berechnung der Schätzfunktion wird oft vorausgesetzt, dass die Zufallsvariablen $X_{i}$ unabhängig voneinander und identisch verteilt sind, also die gleiche Verteilung und die gleichen Verteilungsparameter besitzen.

Ausgewählte Schätzfunktionen

In der statistischen Praxis wird oft nach den folgenden Parametern der Grundgesamtheit gesucht:

den Mittelwert $\mu$ und
der Varianz $\sigma ^{2}$ eines metrischen Merkmals sowie
dem Anteilswert $\pi$ einer dichotomen Grundgesamtheit.

Schätzfunktionen und Schätzwert für den Mittelwert

Der Erwartungswert $\mu$ wird in der Regel mit dem arithmetischen Mittel der Stichprobe geschätzt:

Schätzfunktion	Schätzwert
${\overline {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}$	${\hat {\mu }}={\overline {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}$

Ist die Verteilung symmetrisch, kann auch der Median der Stichprobe als Schätzwert für den Erwartungswert verwendet werden:

Schätzfunktion	Schätzwert
$Z=X_{\left\lfloor {\frac {n+1}{2}}\right\rfloor }$	${\hat {\mu }}=z=x_{\left\lfloor {\frac {n+1}{2}}\right\rfloor }$

wobei $\left\lfloor \;\right\rfloor$ die untere Gaußklammer bezeichnet. Der Median ist also der Wert derjenigen Zufallsvariable, die nach Sortierung der Daten "in der Mitte" liegt. Es befinden sich also zahlenmäßig genauso viele Werte oberhalb wie unterhalb des Median.

Welche Schätzfunktion im Falle symmetrischer Verteilungen besser ist, hängt von der betrachteten Verteilungsfamilie ab.

Schätzfunktionen und Schätzwert für die Varianz

Für die Varianz der Grundgesamtheit $\sigma ^{2}$ verwendet man als Schätzfunktion meist die korrigierte Stichprobenvarianz:

Schätzfunktion	Schätzwert
$S_{n}^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(X_{i}-{\overline {X}})^{2}$	${\hat {\sigma }}^{2}=s_{n}^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}$

Typische andere Vorfaktoren sind auch ${\frac {1}{n}}$ und ${\frac {1}{n+1}}$ . Alle diese Schätzer sind zwar asymptotisch äquivalent, werden aber je nach Art der Stichprobe unterschiedlich benutzt (siehe auch Stichprobenvarianz (Schätzfunktion)).

Schätzfunktionen und Schätzwert für den Anteilswert

Man betrachtet hier das Urnenmodell mit zwei Sorten Kugeln. Es soll der Anteilswert der Kugeln erster Sorte in der Grundgesamtheit geschätzt werden. Als Schätzfunktion verwendet man den Anteil der Kugeln erster Sorte in der Stichprobe.

Schätzfunktion	Schätzwert
$\Pi ={\frac {X}{n}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}$	${\hat {\pi }}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}$

mit : Zahl der Kugeln erster Sorte in der Stichprobe und $X_{i}$ eine binäre Zufallsvariable: Kugel der ersten Sorte in der -ten Ziehung gezogen ( $X_{i}=1$ ) oder nicht gezogen ( $X_{i}=0$ ).

Die Verteilung von $\Pi$ ist eine Binomialverteilung im Modell mit Zurücklegen und eine hypergeometrische Verteilung im Modell ohne Zurücklegen.

Verteilung der Schätzfunktionen

Die Verteilung der Schätzfunktionen hängt natürlich von der Verteilung des Merkmals in der Grundgesamtheit ab.

Seien $X_{1},X_{2},\dots ,X_{n}$ unabhängig und identisch normalverteilte Zufallsvariablen mit Erwartungswert $\mu$ und Varianz $\sigma ^{2}$ . Der Schätzer ${\overline {X}}$ (Stichprobenmittel) als lineare Transformation der $X_{i}$ besitzt dann die Verteilung

${\overline {X}}\sim {\mathcal {N}}\left(\mu ;{\frac {\sigma ^{2}}{n}}\right)$ .

Der Varianzschätzer $S_{n}^{2}$ enthält eine Quadratsumme von bezüglich ${\overline {X}}$ zentrierten normalverteilten Zufallsvariablen. Deshalb ist der Ausdruck

${\frac {(n-1)S_{n}^{2}}{\sigma ^{2}}}\sim \chi ^{2}(n-1)$

Chi-Quadrat-verteilt mit (n-1) Freiheitsgraden.

Ist die Verteilung des Merkmals unbekannt, kann bei Vorliegen der Voraussetzung des zentralen Grenzwertsatzes die Verteilung der Schätzfunktion näherungsweise mit der Normalverteilung oder einer ihrer abgeleiteten Verteilungen angegeben werden.

Gütekriterien von Schätzfunktionen

Wahrscheinlichkeitsdichten für die konsistenten Schätzfunktionen $g_{n}$ (

). Mit steigendem Stichprobenumfang wird der unbekannte Parameter $\gamma$ immer genauer geschätzt.

Erwartungstreue

Eine erwartungstreue Schätzfunktion ist im Mittel (Erwartungswert) gleich dem wahren Parameter $\gamma$ :

$\ \operatorname {E} (g_{n})=\gamma$ .

Weicht $\ \operatorname {E} (g_{n})$ hingegen systematisch von $\gamma$ ab, ist der Schätzer verzerrt (englisch biased). Die Verzerrung eines Schätzers $\operatorname {Bias} (g_{n})$ errechnet sich dabei zu

$\operatorname {Bias} (g_{n})=\operatorname {E} (g_{n})-\gamma =\operatorname {E} (g_{n}-\gamma )$ .

Für eine lediglich asymptotisch erwartungstreue Schätzfunktion dagegen muss nur gelten:

$\lim _{n\to \infty }\operatorname {E} (g_{n})=\gamma$

Konsistenz

Eine Schätzfunktion heißt konsistent, wenn für jedes $\varepsilon >0$ (Infinitesimalzahl) gilt:

$\lim _{n\to \infty }P(|g_{n}-\gamma |>\varepsilon )=0$ .

mit $g_{n}=g(X_{1},X_{2},\dotsc ,X_{n})$ . Man spricht hier von stochastischer Konvergenz.

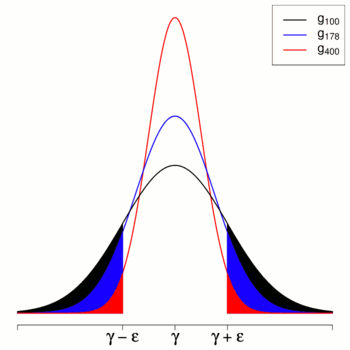
Die Grafik rechts illustriert den Prozess: Für jedes $\varepsilon >0$ müssen die ausgefüllten Flächen mit steigendem Stichprobenumfang immer kleiner werden.

Mit einfachen Worten: Eine konsistente Schätzfunktion nähert sich mit wachsendem immer mehr dem wahren Parameter $\gamma$ an (schätzt den wahren Parameter immer genauer).

Konsistente Schätzfunktionen müssen daher mindestens asymptotisch erwartungstreu (s.o.) sein.

Diese Eigenschaft ist grundlegend für die gesamte induktive Statistik; sie garantiert, dass eine Erhöhung des Stichprobenumfangs genauere Schätzungen, kleinere Konfidenzintervalle oder kleinere Annahmebereiche der $H_{0}$ in Hypothesentests ermöglicht.

Minimale Varianz, Effizienz

Die Schätzfunktion soll eine möglichst kleine Varianz haben. Die Schätzfunktion $g_{n}^{*}$ aus allen erwartungstreuen Schätzfunktionen $g_{n}$ , welche die kleinste Varianz hat, wird dabei als effiziente, beste oder wirksamste Schätzfunktion bezeichnet:

$\operatorname {Var} (g_{n}^{*})\leq \min _{g_{n}}\operatorname {Var} (g_{n})$ .

Unter bestimmten Bedingungen kann durch die Cramér-Rao-Ungleichung auch eine untere Grenze für $\operatorname {Var} (g_{n})$ angegeben werden. Das heißt, für eine Schätzfunktion kann gezeigt werden, dass es keine effizienteren Schätzfunktionen geben kann; höchstens noch genauso effiziente Schätzfunktionen.

Mittlerer quadratischer Fehler

Die Genauigkeit einer Schätzfunktion bzw. eines Schätzers wird oft durch seinen mittleren quadratischen Fehler (englisch mean squared error) ausgedrückt. Eine (dabei nicht notwendigerweise auch erwartungstreue) Schätzfunktion sollte daher stets einen möglichst kleinen mittleren quadratischen Fehler aufweisen, der sich rechnerisch als Erwartungswert der quadratischen Abweichung des Schätzers $g_{n}$ vom wahren Parameter $\gamma$ bestimmen lässt:

$\mathrm {MSE} (g_{n})=\operatorname {E} {\bigl [}(g_{n}-\gamma )^{2}{\bigr ]}={\bigl (}\operatorname {E} [g_{n}-\gamma ]{\bigr )}^{2}+\operatorname {E} {\bigl [}(g_{n}-E(g))^{2}{\bigr ]}=(\operatorname {Bias} (g_{n}))^{2}+\operatorname {Var} (g_{n})$

Wie zu sehen, ist der mittlere quadratische Fehler eines nicht erwartungstreuen Schätzers die Summe seiner Varianz und des Quadrats der Bias (Verzerrung); für erwartungstreue Schätzer dagegen sind Varianz und MSE gleich groß.

Siehe auch

Statistische Tests

Basierend auf einem Artikel in:

Wikipedia.de