Riemannsche Zahlenkugel

Auf der riemannschen Zahlenkugel sind die komplexen Zahlen einschließlich ∞ darstellbar.

stereographische Rückprojektionen der komplexen Zahlen und auf die Punkte $\alpha$ und $\beta$ der riemannschen Zahlenkugel

In der Mathematik ist die riemannsche Zahlenkugel $\hat{\C}= \mathbb{C}\cup\{ \infty\}$ die riemannsche Fläche, die sich aus der Hinzunahme eines Punktes in der Unendlichkeit zu der komplexen Ebene ergibt. Sie geht zurück auf Bernhard Riemann.

Weiter wird auf der riemannschen Zahlenkugel wie folgt eine Topologie definiert: Offene Mengen sind einerseits die offenen Mengen in $\mathbb{C}$ und andererseits die bezüglich $\mathbb{C}\cup\{ \infty\}$ gebildeten Komplemente von kompakten Teilmengen von $\mathbb{C}$ . Der so definierte topologische Raum stellt eine Kompaktifizierung der komplexen Ebene dar. Topologisch ist sie äquivalent zur Einheitskugel $S^{2}$ . Mit der chordalen Metrik wird die Zahlenkugel zu einem metrischen Raum. Diese Metrik induziert die gleiche Topologie, die durch die Einpunktkompaktifizierung auf die Zahlenkugel induziert wird.

Die komplexe Struktur der riemannschen Zahlenkugel wird durch zwei Karten gegeben. Die erste ist auf $\mathbb {C}$ definiert und ist die Identität. Die zweite ist auf der Umgebung $[\mathbb C \cup \{\infty\}] \setminus \{0\}$ des unendlich fernen Punkts definiert durch

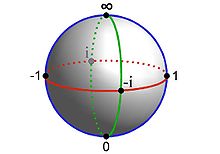
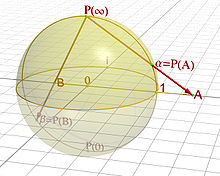
$z \mapsto \begin{cases} \frac 1z, & \text{falls } z \in \mathbb C,\\ 0, & \text{falls }z = \infty. \end{cases}$

Anschaulich handelt es sich um eine Kugel vom Radius 1, deren Nordpol auf (0,0,1) liegt (man darf die Kugel beliebig wählen, solange ihr Nordpol (0,0,1) ist). Dem unendlich fernen Punkt $\infty$ wird dieser Nordpol der Kugel zugeordnet und jedem Punkt der komplexen Zahlenebene der von verschiedene Schnittpunkt der Kugeloberfläche mit der Geraden durch (stereografische Projektion).

Die Automorphismen, also die biholomorphen Abbildungen der riemannschen Zahlenkugel auf sich selbst, bilden die Gruppe der Möbiustransformationen.

Siehe auch

Projektiver Raum

Basierend auf einem Artikel in:

Wikipedia.de