
De-Casteljau-Algorithmus
Der Algorithmus von de Casteljau ermöglicht die effiziente Berechnung einer beliebig genauen Näherungsdarstellung von Bézierkurven durch einen Polygonzug. Der Algorithmus wurde Anfang der 1960er Jahre von Paul de Faget de Casteljau bei Citroën entwickelt.
Idee
Der Algorithmus von de Casteljau beruht darauf, dass eine Bézierkurve geteilt und durch zwei aneinandergesetzte Bézierkurven dargestellt werden kann. Diese Unterteilung kann rekursiv fortgesetzt werden. Das Kontrollpolygon der zusammengesetzten Bézierkurve nähert sich dabei der Originalkurve an. Nach ausreichend vielen Verfeinerungsschritten kann der entstandene Polygonzug als Näherung für die Originalkurve verwendet werden. Ein Verfeinerungsschritt, der das Kontrollpolygon einer Ausgangskurve in ein Kontrollpolygon einer zusammengesetzten Kurve zerlegt, besteht nur aus wenigen einfachen Teilungen von Polygonkanten.
Darüber hinaus ermöglicht der Algorithmus die schnelle Bestimmung jedes einzelnen Punktes auf der Bézierkurve durch seine parametrische Darstellung.
Erweiterungen findet der Algorithmus im Blossoming wie auch im fokalen Algorithmus von de Casteljau.
Algorithmus
Gegeben sind die Kontrollpunkte
der Ausgangskurve
mit
.
Von den Kontrollpunkten der Ausgangskurve
liegen im Allgemeinen nur
und
auf der Kurve. Der Algorithmus berechnet im ersten Schritt einen weiteren Punkt
der Kurve. Dabei kann
frei gewählt werden. Die Kurve wird im Weiteren an diesem Punkt
geteilt. Es bietet sich daher die Wahl von
an, weil dies eine gleichmäßige Aufteilung und damit eine schnelle Annäherung
des Kontrollpolygons an die Ausgangskurve gewährleistet.
Bilden von Teilverhältnissen
Statt durch direktes Einsetzen von
in die Gleichung der Kurve
geschieht die Berechnung von
über die Konstruktion von Punkten
aus den gegebenen Kontrollpunkten
.
Die Konstruktion startet mit den Ausgangspunkten
.
Aus diesen werden durch Teilen der Verbindungslinien
im Verhältnis
neue Punkte
konstruiert. Der Punkt
berechnet sich nach der intuitiv einsichtigen Formel:
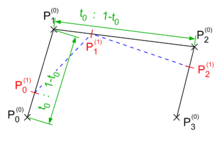
In nebenstehender Abbildung sind die Punkte ,
die aus den Ausgangspunkten
hervorgegangen sind, rot eingezeichnet. Durch Fortsetzen der
Berechnungsvorschrift werden in gleicher Weise Punkte
bestimmt. Zur Berechnung von
werden dazu die blau gestrichelten Verbindungslinien der im ersten Schritt
berechneten Punkte
im selben Verhältnis geteilt usw.
Konstruktion eines Kurvenpunktes
Es gilt die folgende Aussage (siehe Beweis der Punktkonstruktion):
Das heißt, dass der Punkt ,
welcher in der
ten
Iteration durch fortgesetztes Streckenteilen konstruiert wird, ein Punkt der
Kurve ist. Das Teilungsverhältnis
bestimmt dabei seine Lage auf der Kurve.
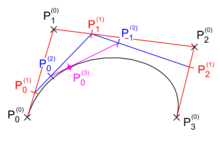
In nebenstehender Abbildung ist die Konstruktion für
vollständig durchgeführt. Der Punkt
,
der durch dreifache Anwendung der Teilungsvorschrift aus den Ausgangspunkten
hervorgegangen ist, liegt auf der gesuchten Kurve.
Die bei weitem interessantere Aussage ist aber, dass dieser Punkt
die Kurve
in zwei Bézierkurven
und
teilt und dass die Punkte
das Kontrollpolygon von
und die Punkte
das Kontrollpolygon von
bilden.
Teilen in zwei Bézierkurven
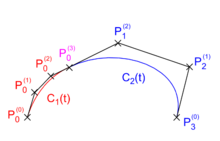
Nebenstehende Abbildung zeigt die Zerlegung von
in
und
für
.
Dabei bilden die Punkte
,
,
und
das Kontrollpolygon von
und entsprechend die Punkte
,
,
und
das Kontrollpolygon von
.
An der Abbildung erkennt man außerdem, warum in der Regel ein
Teilungsverhältnis von
verwendet wird. Da in diesem Beispiel ein Teilungsverhältnis kleiner ½ verwendet
wurde, teilt sich die Kurve
in einem ungleichen Verhältnis in eine kurze Kurve
und eine lange Kurve
auf. Der kürzere Teil ist viel besser an sein Kontrollpolygon angenähert als der
längere. Möchte man (bei ungefähr gleich langen Strecken des
Ausgangskontrollpolygons) eine gleichmäßige Näherung erreichen, eignet sich dazu
das Teilungsverhältnis
.
Die Unterteilung der Kurven wird so lange fortgesetzt, bis sie hinreichend genau durch ihre Kontrollpolygone angenähert sind.
Pseudocode
Zu Beginn liegen die Punkte des Kontrollpolygons in einem Feld
vor. Bei gegebenem Parameter
wird der Punkt
folgendermaßen berechnet:
BEGIN
FOR i:=0..n
 FOR j:=1..n
FOR i:=0..(n-j)
// Unterteilung mit Faktor t
FOR j:=1..n
FOR i:=0..(n-j)
// Unterteilung mit Faktor t
 RETURN
RETURN  END
END
Der obige Algorithmus ist insoweit unvollständig, dass nur der Punkt
bestimmt, aber keine fortgesetzte Unterteilung von
durchgeführt wird. Der Algorithmus ist nicht speichereffizient, da für alle
neue Speicherplätze belegt werden.
Beweis der Punktkonstruktion
Die Aussage, dass über -fach
fortgesetzte Streckenteilung ein weiterer Punkt der Kurve konstruiert werden
kann, lässt sich über Lösen der Rekursion
beweisen, die
definiert.
Rekursionsgleichung
Die Rekursionsgleichung definiert die Punkte
in Abhängigkeit von den in der letzten Iteration berechneten Punkten
.
Den Start der Rekursion bilden die Punkte
:
Zu beweisende Aussage
Zu beweisen ist die Aussage, dass der Punkt
ein Punkt der Kurve an der Stelle
ist:
Verallgemeinerung der Aussage
Um eine Lösung der Rekursion für den speziellen Punkt
zu finden, wird eine geschlossene Form für alle Punkte
der Rekursion gesucht und gezeigt, dass diese insbesondere für
das gesuchte Resultat liefert. Der Beweis für
wird über vollständige
Induktion mit folgender Induktionsannahme geführt:
.
Der Induktionsschritt ist dann eine gradlinige Rechnung, bei der Aussagen über Binomialkoeffizienten benutzt werden.
Anwendung
Mit Hilfe des Algorithmus von de Casteljau ist es möglich, Näherungen von Bézierkurven durch gerade Linien zu errechnen. Dadurch kann eine Bézierkurve effizient mit dem Rechner gezeichnet werden.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 29.10. 2020