Trapezregel

Die Trapezregel beschreibt ein mathematisches Verfahren zur numerischen Annäherung des Integrals einer Funktion f(x) im Intervall [a, b] (Numerische Quadratur).

Dazu ersetzt man die Fläche unter der Kurve y=f(x) im gegebenen Intervall durch ein Trapez oder mehrere gleich breite Trapeze.

Es gibt verschiedene Möglichkeiten zur Bestimmung dieser Trapeze: Man kann die Kurve zum Beispiel näherungsweise durch eine Sehne zwischen den Funktionswerten an den Stellen und ersetzen. Dies führt zur Sehnentrapezformel. Man kann aber auch in der Mitte des Intervalls die Tangente an die Funktion legen und erhält dann die Tangententrapezformel oder Mittelpunktsregel.

Beispiel

$J(f) = \int_{0}^{2}3^{3x-1} \, \mathrm{d}x = \frac{3^{3x-2}}{\ln(3)}\Big|_0^2 =\frac{728}{9 \ln(3)} = 73{,}6282396649\dots$

Mit Hilfe der im Folgenden erklärten Trapezformeln soll dieses bestimmte Integral näherungsweise berechnet werden.

Sehnentrapezformel

Sehnentrapez

$J(f) = \int_a^b f(x)\, \mathrm dx = T(f) + E(f).$

Das Trapez wird gebildet aus der Grundlinie [a,b] (dem Intervall auf der -Achse), den senkrechten Geraden [a,f(a)] und [b,f(b)] sowie der Sehne als Verbindungsgerade zwischen f(a) und f(b) . Diese Sehne ersetzt die Kurve $f(x), x\in[a,b]$ .

Die Sehnentrapezformel ergibt sich aus dem Flächeninhalt des beschriebenen Trapezes:

$T(f) = (b-a)\frac{f(a)+f(b)}{2}.$

Diese Formel – und auch die folgenden – kann man herleiten aus der „Allgemeinen Quadraturformel für eine Teilfläche“ (siehe Numerische Quadratur).

Ist zweimal stetig differenzierbar in [a,b] , dann gilt für das Restglied E(f) folgende Abschätzung (siehe Numerische Quadratur):

$\left|E(f)\right| \le\frac{(b-a)^3}{12} \max_{a\le x\le b} \left|f''(x)\right|.$

Ist zusätzlich noch reellwertig, dann gilt mit einer Zwischenstelle $\zeta\in[a,b]$

$E(f) = -\frac{(b-a)^3}{12} f''(\zeta).$

Das Vorzeichen in dieser Formel kann man sich wie folgt geometrisch plausibel machen: Falls die Funktion f(x) , wie in der obigen Abbildung des Sehnentrapezes, streng konkav ist, gilt f''(x)<0 für alle $x\in[a,b]$ und daher auch für die Zwischenstelle $\zeta\in[a,b]$ . Somit folgt, dass E(f)=J(f)-T(f)>0 , d.h. die gesuchte Fläche J(f) ist größer als die Trapezfläche T(f) , wie auch die Abbildung zeigt.

Die Abhängigkeit des Fehlers von der 2. Ableitung von f(x) bedeutet, dass die Formel für Geraden exakt ist, was auch anschaulich klar ist. Der Genauigkeitsgrad ist somit 1.

Angewandt auf obiges Beispiel:

$T(f) = (2-0)\frac{f(0)+f(2)}{2} = \frac{730}3 = 243{,}\bar{3}.$

Wegen $f''(x)=3^{3x+1} \cdot \ln(3)^2>0$ folgt aus obiger Formel, dass die gesuchte Fläche J(f) kleiner ist als die Trapezfläche T(f) , in Übereinstimmung mit den errechneten Zahlen.

Zusammengesetzte Sehnentrapezformel

$J(f) = \int_a^b f(x)\,\mathrm dx = T^{(n)}(f) + E^{(n)}(f).$

Um das Integral noch besser annähern zu können, unterteilt man das Intervall [a,b] in nebeneinanderliegende gleich große Teilintervalle der Länge $h=\tfrac{b-a}n$ . In jedem Teilintervall wendet man die Sehnentrapezformel für die einzelnen Teilflächen an und addiert danach die entstandenen Näherungen. Damit erhält man die summierte (bzw. zusammengesetzte) Sehnentrapezformel:

$T^{(n)}(f)=h\left(\frac 12 f(a) + \frac 12 f(b) + \sum_{i=1}^{n-1} f(a+ih)\right)$

mit

$h = \frac{b-a}n.$

Angewandt auf obiges Beispiel:

Sei die Schrittweite $h = \tfrac 13$ und damit n = 6 . Dann ist

$\begin{align} T^{(6)}(f) &= \frac 13\left(\frac 12f(0) + f\left(\frac 13\right) + f\left(\frac 23\right) + f(1) + f\left(\frac 43\right) + f\left(\frac 53\right) + \frac 12 f(2) \right)\\ &= \frac{728}9 = 80{,}\bar{8}. \end{align}$

Sei die Schrittweite $h = \tfrac 16$ und damit n = 12 . Dann ist

${\begin{aligned}T^{(12)}(f)&={\frac {1}{6}}\left({\frac {1}{2}}f(0)+f\left({\frac {1}{6}}\right)+f\left({\frac {2}{6}}\right)+f\left({\frac {3}{6}}\right)+...+f\left({\frac {10}{6}}\right)+f\left({\frac {11}{6}}\right)+{\frac {1}{2}}f(2)\right)\\&={\frac {T^{(6)}(f)}{2}}+{\frac {1}{6}}\cdot \left(f\left({\frac {1}{6}}\right)+f\left({\frac {3}{6}}\right)+f\left({\frac {5}{6}}\right)+f\left({\frac {7}{6}}\right)+f\left({\frac {9}{6}}\right)+f\left({\frac {11}{6}}\right)\right)\\&={\frac {728+364{\sqrt {3}}}{18}}=75{,}4703608\dotso \end{aligned}}$

Man sieht hier den Vorteil der Sehnentrapezregel: Verdoppelt man die Anzahl der Intervalle, so kann auf die vorangegangene Rechnung zurückgegriffen werden. Das ist bei der Tangententrapezregel (s.u.) nicht der Fall. Das ist einer der Gründe, warum die Romberg-Integration auf der Sehnentrapezregel als Basis aufbaut.

Die allgemeine Formel lautet:

$T^{(2n)}(f)= \frac{T^{(n)}(f)}{2}+ \frac{h}{2} \cdot \sum_{i=1}^n f\left(a \ - \frac{h}{2} + i\cdot h \right).$

Fehlerabschätzung

Die Fehlerabschätzung für das Restglied lautet

$\left| E^{(n)}(f)\right|\le\frac{(b-a)}{12} h^2 \max_{a\le x\le b} \left|f''(x)\right|$

bzw. für reellwertige Funktionen mit einer Zwischenstelle $\zeta$ aus dem Intervall [a,b]

$E^{(n)}(f)= -\frac{(b-a)}{12} h^2 f''(\zeta).$

Der Faktor h^2 in obiger Formel bedeutet, dass bei einer Halbierung der Schrittweite (Verdoppelung der Intervalle), wie es beim Romberg-Verfahren mit der Romberg-Folge der Fall ist, der Fehler in etwa um den Faktor 4 kleiner wird, wie auch nachfolgendes Beispiel zeigt:

Angewandt auf obiges Beispiel:

Mit $f''(x)=3^{3x+1} \cdot \ln(3)^2$ folgt

$\max_{0\le x\le 2} \left|f''(x)\right|=3^{3\cdot2+1} \cdot \ln(3)^2=3^7\cdot(\ln(3))^2$

und somit die Fehlerabschätzung

$\left| E^{(6)}(f)\right|\le\frac{2}{12} \cdot \left(\frac{1}{3}\right)^{2}\cdot3^7\cdot(\ln(3))^2=\frac{3^4\cdot(\ln(3))^2}{2}= 48{,}88\dots$ ,

die erwartungsgemäß einen größeren Wert ergibt als den exakten Wert

$E^{(6)}(f)=\frac{728}{9}\cdot\frac{1-\ln(3)}{\ln(3)}=-7{,}26\dots.$

Analog erhält man die Fehlerabschätzung

$\left| E^{(12)}(f)\right|\le\frac{2}{12} \cdot \left(\frac{1}{6}\right)^{2}\cdot3^7\cdot(\ln(3))^2=\frac{3^4\cdot(\ln(3))^2}{8}= 12{,}22\dots$ ,

die erwartungsgemäß einen größeren Wert ergibt als den exakten Wert

$E^{(12)}(f)=\frac{182}{9\ln(3)}\cdot(4-2\ln(3)-\ln(3)\sqrt 3)=-1{,}842\dots.$

Es gilt

$\left|E^{(12)}(f)\right|=1,842\dots \approx {\frac {\left|E^{(6)}(f)\right|}{4}}={\frac {7{,}26\dots }{4}}=1{,}815\dots .$

Fehlerschätzung

Rechnet man die Sehnentrapezformel zweimal mit 2 verschiedenen Anzahlen von Intervallen $n \ne m$ , so erhält man folgende Fehlerschätzung:

$E^{(n)}(f)\approx \frac{m^2}{m^2-n^2}\left(T^{(m)}(f)-T^{(n)}(f)\right).$

Speziell bei der Verdoppelung der Intervalle m=2n (Halbierung der Schrittweite) erhält man die Fehlerschätzung:

$E^{(n)}(f)\approx \frac 43 \left(T^{(2n)}(f)-T^{(n)}(f)\right)$

Angewandt auf das obige Beispiel erhält man

${\begin{aligned}E^{(6)}(f)=-7{,}26\dots &\approx {\frac {4}{3}}\left(T^{(12)}(f)-T^{(6)}(f)\right)\\&={\frac {4}{3}}\left({\frac {728+364{\sqrt {3}}}{18}}-{\frac {728}{9}}\right)={\frac {2}{27}}(364{\sqrt {3}}-728)=-7{,}2247\dots .\end{aligned}}$

Asymptotische Fehlerentwicklung

Wir bestimmen im Folgenden die Art des Fehlers der Trapezsumme und im Speziellen ihre Abhängigkeit von der Schrittweite , wobei das Integral $\int_a^b f(x) \, \mathrm dx$ bestimmt werden soll.

Seien dazu

die Schrittweite: $h={\frac {b-a}{n}}$ mit $n\in \mathbb {N}$
Trapezsumme ist -abhängig: $T=T_{n}(h)={\frac {h}{2}}\left(f(a)+f(b)+2\sum _{i=1}^{n-1}f(a+ih)\right)$
der Integrand ist stetig-differenzierbar: $f\in C^{2m+1}([a,b])$ mit $m\in\N$ .

Dann gilt das folgende Fehlerverhalten für die Trapezsumme

$T_{n}(h)=\int _{a}^{b}f(x)\,\mathrm {d} x+\sum _{k=1}^{m}\tau _{2k}h^{2k}+R_{2m+2}(h)h^{2m+2}\,,$

wobei die folgenden Definitionen gelten

$\tau _{2k}={\frac {B_{2k}}{(2k)!}}\left(f^{(2k-1)}(b)-f^{(2k-1)}(a)\right)\,,\quad R_{2m+2}(h)=-\int _{a}^{b}K_{2m+2}(t,h)f^{(2m)}(t)\,\mathrm {d} t\,.$

Weiterhin sind die $B_{{2k}}$ durch die Bernoulli-Zahlen gegeben und der Koeffizient des Resttermes kann gleichmäßig in abgeschätzt werden kann. Es gilt also

$\exists C_{2m+2}\geq 0\;\forall h={\frac {b-a}{n}}\,:\quad |R_{2m+2}(h)|\leq C_{2m+2}\,.$

Tangententrapezformel oder Mittelpunktsregel

Tangententrapez

Mittelpunktsregel

$J(f) = \int_{a}^{b}f(x)\, \mathrm{d}x = M(f) + E(f).$

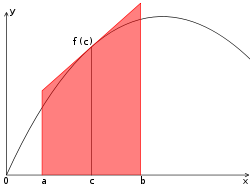
Das Trapez wird gebildet aus der Grundlinie [a,b] (dem Intervall auf der -Achse), den senkrechten Geraden [a,f(a)] und [b,f(b)] sowie der Tangente an f(x) in der Mitte des Intervalls [a,b] . Diese Tangente ersetzt die Kurve $f(x), x\in[a,b]$ .

Die Tangententrapezformel ergibt sich aus dem Flächeninhalt des beschriebenen Trapezes:

$M(f) = (b - a) \ f\left(\frac{a + b}{2} \right).$

Diese Formel – und auch die folgenden – kann man herleiten aus der „Allgemeinen Quadraturformel für eine Teilfläche“ (siehe Numerische Quadratur).

Ist zweimal stetig differenzierbar in [a,b] , dann gilt für das Restglied E(f) folgende Abschätzung (siehe Numerische Quadratur):

$\left| E(f) \right| \le \frac{(b-a)^3}{24} \max_{a\le x \le b} {\left| f''(x) \right|}.$

Ist zusätzlich noch reellwertig, dann gilt mit einer Zwischenstelle $\zeta\in[a,b]$ :

$E(f) = \frac{(b-a)^3}{24} \cdot f''(\zeta).$

Das Vorzeichen in dieser Formel kann man sich wie folgt geometrisch plausibel machen: Falls die Funktion f(x) , wie in der obigen Abbildung des Tangententrapezes, streng konkav ist, gilt f''(x)<0 für alle $x\in[a,b]$ und daher auch für die Zwischenstelle $\zeta\in[a,b]$ . Somit folgt, dass E(f)=J(f)-M(f)<0 , d.h. die gesuchte Fläche J(f) ist kleiner als die Trapezfläche M(f) , wie auch die Abbildung zeigt.

Die Abhängigkeit des Fehlers von der 2. Ableitung von f(x) bedeutet, dass die Formel für Geraden exakt ist, was auch anschaulich klar ist. Der Genauigkeitsgrad ist somit 1.

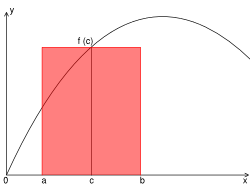
Dreht man im obenstehenden Bild der Tangententrapezregel die Tangente im Punkt (c,f(c)) im Uhrzeigersinn bis man eine horizontale Gerade erhält, so entsteht ein Rechteck mit der gleichen Fläche. Die so erhaltene Regel (Mittelpunktsregel) ist somit eine andere geometrische Deutung der gleichen Quadraturformel.

Angewandt auf obiges Beispiel:

$M(f) = (2-0) \cdot f(1) = 18.$

Wegen $f''(x)=3^{3x+1} \cdot \ln(3)^2>0$ folgt aus obiger Formel, dass die gesuchte Fläche J(f) größer ist als die Trapezfläche M(f) , in Übereinstimmung mit den errechneten Zahlen.

Zusammengesetzte Tangententrapezformel oder Mittelpunktsregel

$J(f) = \int_a^b f(x)\,\mathrm dx = M^{(n)}(f) + E^{(n)}(f).$

Um das Integral noch besser annähern zu können unterteilt man das Intervall [a,b] in nebeneinanderliegende gleich große Teilintervalle der Länge $h=\tfrac{b-a}n$ . In jedem Teilintervall wendet man die Tangententrapezformel für die einzelnen Teilflächen an und addiert danach die entstandenen Näherungen. Damit erhält man die summierte (bzw. zusammengesetzte) Tangententrapezformel:

$M^{(n)}(f)=h \cdot \sum_{i=1}^n f\left(a \ - \frac{h}{2} + i\cdot h \right)$

mit

$h = \frac{(b - a)}{n}.$

Angewandt auf obiges Beispiel:

Sei die Schrittweite $h = \tfrac 13$ und damit n = 6

$M^{(6)}(f) = \frac{1}{3} \cdot \left(f\left(\frac{1}{6}\right) + f\left(\frac{3}{6}\right) + f\left(\frac{5}{6}\right) + f\left(\frac{7}{6}\right) + f\left(\frac{9}{6}\right) + f\left(\frac{11}{6}\right) \right) = \frac{364 \sqrt 3}{9} = 70{,}05183266\dots$

Sei die Schrittweite $h = \tfrac 16$ und damit n = 12 . Dann ist

${\begin{aligned}M^{(12)}(f)&={\frac {1}{6}}\cdot \left(f\left({\frac {1}{12}}\right)+f\left({\frac {3}{12}}\right)+f\left({\frac {5}{12}}\right)+\dots +f\left({\frac {21}{12}}\right)+f\left({\frac {23}{12}}\right)\right)\\&={\frac {3^{6}-1}{2\cdot 3^{\frac {7}{4}}({\sqrt {3}}-1)}}=72{,}71063941368\dots .\end{aligned}}$

Im Gegensatz zur Sehnentrapezregel kann bei der Tangententrapezregel bei Verdoppelung der Anzahl der Intervalle auf die vorangegangene Rechnung nicht zurückgegriffen werden.

Fehlerabschätzung

Die Fehlerabschätzung für das Restglied lautet:

$\left| E^{(n)}(f) \right| \le {(b - a) \over 24} \ h^2 \max_{a\le x \le b} {\left| f''(x) \right|}$

bzw. für reellwertige Funktionen mit einer Zwischenstelle $\zeta\in[a,b]$ :

$E^{(n)}(f)={(b - a) \over 24} \cdot h^2 \cdot f''(\zeta).$

Der Faktor h^2 in obiger Formel bedeutet, dass bei einer Halbierung der Schrittweite (Verdoppelung der Intervalle), der Fehler in etwa um den Faktor 4 kleiner wird, wie auch nachfolgendes Beispiel zeigt:

Angewandt auf obiges Beispiel:

Mit $f''(x)=3^{3x+1} \cdot \ln(3)^2$ folgt

$\max_{0\le x\le 2} \left|f''(x)\right|=3^{3\cdot2+1} \cdot \ln(3)^2=3^7\cdot(\ln(3))^2$

und somit die Fehlerabschätzung

$\left| E^{(6)}(f)\right|\le\frac{2}{24} \cdot \left(\frac{1}{3}\right)^{2}\cdot3^7\cdot(\ln(3))^2=\frac{3^4\cdot(\ln(3))^2}{4}= 24{,}44\dots$ ,

die erwartungsgemäß einen größeren Wert ergibt als den exakten Wert

$E^{(6)}(f)=\frac{364}{9}\cdot\frac{2-\ln(3)\sqrt 3}{\ln(3)}=3{,}5764\dots.$

Analog erhält man als Fehlerabschätzung

$\left| E^{(12)}(f)\right|\le\frac{2}{24} \cdot \left(\frac{1}{6}\right)^{2}\cdot3^7\cdot(\ln(3))^2=\frac{3^4\cdot(\ln(3))^2}{16}= 6{,}11\dots$ ,

die erwartungsgemäß einen größeren Wert ergibt als den exakten Wert

$E^{(12)}(f)=0{,}9176\dots .$

Es gilt

$\left|E^{(12)}(f)\right|=0{,}9176\dots \approx {\frac {\left|E^{(6)}(f)\right|}{4}}={\frac {3{,}5764\dots }{4}}=0{,}8941\dots .$

Fehlerschätzung

Rechnet man die Tangententrapezformel zweimal mit zwei verschiedenen Anzahlen von Intervallen $n \ne m$ , so erhält man wie bei der Sehnentrapezregel folgende Fehlerschätzung:

$E^{(n)}(f)\approx {\frac {m^{2}}{m^{2}-n^{2}}}\left(M^{(m)}(f)-M^{(n)}(f)\right)$ .

Speziell bei der Verdoppelung der Intervalle m=2n (Halbierung der Schrittweite) erhält man die Fehlerschätzung:

$E^{(n)}(f)\approx {\frac {2^{2}}{2^{2}-1}}\left(M^{(2n)}(f)-M^{(n)}(f)\right)$ .

Angewandt auf das obige Beispiel erhält man

$E^{(6)}(f)=3{,}5764\dotso \approx {\frac {2^{2}}{2^{2}-1}}\left(M^{(12)}(f)-M^{(6)}(f)\right)=3{,}545\dotso$ .

Zusammenhang mit anderen Formeln

Wie man an obigen Beispielen sieht, gilt

$\begin{align} T^{(12)}(f) &= \frac{T^{(6)}(f)}{2}+ \frac{1}{6} \cdot \left(f\left(\frac{1}{6}\right) + f\left(\frac{3}{6}\right) + f\left(\frac{5}{6}\right) + f\left(\frac{7}{6}\right) + f\left(\frac{9}{6}\right) + f\left(\frac{11}{6}\right) \right)\\ &= \frac{T^{(6)}(f)+M^{(6)}(f)}{2}.\\ \end{align}$

Die allgemeine Formel lautet:

$T^{(2n)}(f)= \frac{T^{(n)}(f)}{2}+ \frac{h}{2} \cdot \sum_{i=1}^n f\left(a \ - \frac{h}{2} + i\cdot h \right)= \frac{T^{(n)}(f)+M^{(n)}(f)}{2}.$

Für die Fehlerschätzung der Sehnentrapezregel erhält man somit

$E^{(n)}(f)\approx \frac 43 \left(T^{(2n)}(f)-T^{(n)}(f)\right) = \frac 43 \left(\frac{T^{(n)}(f)+M^{(n)}(f)}{2}-T^{(n)}(f)\right)= \frac 23 \left(M^{(n)}(f)-T^{(n)}(f)\right).$

Addiert man zum Näherungswert $T^{(n)}(f)$ die Fehlerschätzung für $E^{(n)}(f)$ , so erhält man die beiden besseren äquivalenten Formeln:

$T^{(n)}(f)+\frac{2}{3}\left(M^{(n)}(f)-T^{(n)}(f)\right) = \frac 13 \left(T^{(n)}(f)+2M^{(n)}(f)\right).$
Das ist die Formel von $S^{(n)}(f)$ der Simpsonregel. Somit erhält man eine Formel vom Genauigkeitsgrad 3, die Polynome bis zum Grad 3 exakt integriert. Diese liefert i.A. bessere Resultate als $T^{(n)}(f)$ oder $M^{(n)}(f)$ .
$T^{(n)}(f)+\frac{4}{3}\left(T^{(2n)}(f)-T^{(n)}(f)\right) = \frac{4 \cdot T^{(2n)}(f)-T^{(n)}(f)}{3}.$
Das ist die Formel für die 2. Spalte des Rechenschemas der Romberg-Integration bei Verwendung der Romberg-Folge. Somit ist die 2. Spalte des Rombergschemas die Simpsonregel mit dem Genauigkeitsgrad 3.

Angewandt auf obiges Beispiel erhält man mit

$S^{(6)}(f) = \frac 13 \left(T^{(6)}(f)+2M^{(6)}(f)\right) = \frac{4 \cdot T^{(12)}(f)-T^{(6)}(f)}{3} = \frac{728 \cdot (\sqrt 3 + 1)}{27} = 73{,}66418473741264\dots$

eine bessere Näherung für das exakte Integral $J(f) = \int_{0}^{2}3^{3x-1} \, \mathrm{d}x = 73{,}6282396649\dots$

als mit $T^{(6)}(f)= 80{,}\bar{8}, T^{(12)}(f)= 75{,}4703608...$ , oder $M^{(6)}(f)= 70{,}05183266\dots,$

bei gleicher Anzahl auszuwertender Funktionswerte wie $T^{(12)}(f)$ , nämlich 13 Stück.

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de