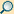Nutation (Physik)
Die Nutation beschreibt die Bewegung eines kräftefreien Kreisels, wenn der Drehimpuls nicht parallel zum minimalen oder maximalen Trägheitsmoment des Kreisels ausgerichtet ist. Bei einem symmetrischen Kreisel überstreicht seine Figurenachse einen Kegel mit dem Drehimpuls als Achse. Aufgrund der Drehimpulserhaltung bleibt der Drehimpuls in Betrag und Richtung konstant. Provozieren kann man die Nutation durch Anstoßen eines stabil um seine Figurenachse rotierenden Kreisels.
Zusätzlich zur Nutation kann ein Kreisel, auf den ein Drehmoment wirkt, noch eine Präzessionsbewegung ausführen.
Symmetrischer Kreisel
Der symmetrische Kreisel ist ein wichtiger Sonderfall mit dem sich die
Betrachtung der Nutation vereinfacht. Eine weitere Vereinfachung entsteht, wenn
das Bezugssystem für momentane Betrachtungen am Kreisel ausgerichtet wird. Dabei
liegt eine Koordinatenachse längs der Figurenachse, womit der Trägheitstensor
als Diagonalmatrix
auftritt. Die nächste Koordinatenachse wird so gewählt, dass eine Ebene
aufgespannt wird, in der sich der Drehimpuls befindet, also der Drehimpulsvektor
in einer Dimension den Wert null annimmt.
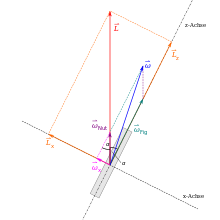
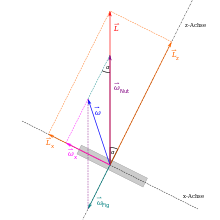
Nun bleiben nur noch zwei variable Komponenten im Drehimpulssatz und eine grafische Herleitung der weiteren Schritte gelingt.
Hier zeigt sich, dass die Winkelgeschwindigkeit nicht parallel zum raumfesten Drehimpuls liegt, sondern davon abweicht und damit sich zeitlich ändert. Durch geschickte Vektorzerlegung kann das Bewegungsverhalten des Kreisels allerdings besser beschrieben werden. Die Vektorkomponente ωFig sei so gewählt, dass sie parallel zur Figurenachse liegt und die zweite Vektorkomponente ωNut sei so gewählt, dass sie parallel zum Drehimpuls liegt. Weil bei der Drehung eines symmetrischen Kreisels um seine Figurenachse sich weder dessen Ausrichtung im Raum noch der Trägheitstensor ändert, gilt die Bewegung ωFig als „neutral“. Viel spannender dagegen ist die Winkelgeschwindigkeit ωNut mit ihr wird der Kreisel samt dem eingangs definierten Koordinatensystem um den Drehimpulsvektor geschwenkt. Damit zeigt sich, dass Figurenachse, Drehimpuls und Winkelgeschwindigkeit des symmetrischen Kreisels in konstanter räumlicher Beziehung zueinanderstehen und stets in einer Ebene liegen. Die Figurenachse und die Winkelgeschwindigkeit überstreichen jeweils den Mantel eines Kegels, in dessen Kegelachse der Drehimpuls liegt.
Anhand der Grafik zur Vektorzerlegung kommt man zunächst auf die folgenden Gleichungen:
Über den Drehimpulssatz ergibt sich durch geschicktes einsetzen:
Wenn gilt ,
dann lässt sich folgende Näherungsrechnung aufstellen:
Ein abgeplatteter Kreisel, der gestoßen wurde, flattert anschließend mit einer Frequenz, die oberhalb seiner Rotationsfrequenz liegt. Durch die hohe Frequenz findet meist eine schnelle Dämpfung der Nutation statt und die Figurenachse richtet sich bald mit dem Drehimpuls aus.
Eine ausführliche mathematische Beschreibung der Kreiselbewegung wird durch die eulerschen Gleichungen ermöglicht.
Bedeutung
- Astronomischen Beobachtungen
- Atomphysik (z. B. MRT)


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 08.01. 2025