Steradiant
| Physikalische Einheit | |
|---|---|
| Einheitenname | Steradiant |
| Einheitenzeichen | |
| Physikalische Größe(n) | Raumwinkel |
| Formelzeichen | |
| Dimension | |
| System | Internationales Einheitensystem |
| In SI-Einheiten | |
| Benannt nach | griechisch στερεός, „räumlich“ und lateinisch radius, „Strahl“ |
| Abgeleitet von | Radiant |
| Siehe auch: Quadratgrad | |
Der Steradiant, auch Sterad, Einheitenzeichen sr, ist eine Maßeinheit für den Raumwinkel. Im Internationalen Einheitensystem (SI) ist er als abgeleitete Maßeinheit enthalten.
Auf einer Kugel mit 1 m Radius
umschließt ein Steradiant eine Fläche
von 1 m² auf der Kugeloberfläche.
Der Raumwinkel der gesamten Kugeloberfläche beträgt 4π sr.
Definition
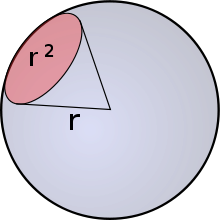
Gegeben sei eine Kugel mit dem Radius .
Dann ist ein Steradiant der Raumwinkel, den von der Mitte der Kugel aus gesehen
eine Kugelkalotte
mit der Fläche
auf der Kugeloberfläche einnimmt. Dieser Raumwinkel lässt sich berechnen als die
Fläche
der Kugelkalotte dividiert
durch das Quadrat des Radius
:
Die Division bewirkt, dass der Raumwinkel nicht vom Radius der betrachteten Kugel abhängt.
- Beispiel
Der Raumwinkel eines Kegels, der aus einer Kugel mit Radius 3 m eine
Teilfläche ()
von 13,5 m2 herausschneidet, beträgt
.
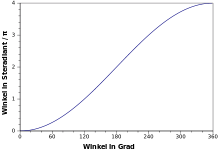
Bezieht sich der Raumwinkel auf einen Kreiskegel
vom Kugelmittelpunkt aus, wie in der Abbildung rechts (kanonischer
Raumwinkel), so kann man ihn im Schnitt durch die Kugelmitte als ebenen Winkel
betrachten. Aus der Beziehung für die Fläche der Kugelkappe des Kegels und dem
Winkel
lässt sich folgender Zusammenhang ableiten:
.
Der Öffnungswinkel
eines Kegels, der den Raumwinkel 1 sr abdeckt, beträgt ca. 65,54°.
Geschichte
Im SI war zunächst offengelassen worden, ob Steradiant und Radiant abgeleitete Einheiten oder Basiseinheiten sind; für beide wurde die Klasse der „ergänzenden Einheiten“ geschaffen. 1980 empfahl das CIPM, diese ergänzenden Einheiten als abgeleitete zu interpretieren. Dem folgte 1995 die 20. Generalkonferenz für Maße und Gewichte (CGPM) und beschloss in Resolution 8 die Aufhebung der Klasse der ergänzenden Einheiten.
Das Einheitenzeichen „sr“ wurde 1950 vom CIPM festgelegt. Früher wurden auch die Zeichen „str“ und „sterad“ benutzt.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 13.07. 2021