Kosmologisches Entfernungsmaß

In der Astronomie werden verschiedene Längenmaße verwendet, um eine Vorstellung von der räumlichen Anordnung astronomischer Objekte zu bekommen. Diese Längenmaße werden auch als Entfernungsmaß bezeichnet.^[1] Neben den bekannteren astronomischen Entfernungsmaßen wie der astronomischen Einheit und dem Lichtjahr gibt es deshalb auch noch verschiedene kosmologische Entfernungsmaße. Auf kosmologischen Längenskalen ist die Entfernungsmessung, wie etwa zu Quasaren oder weit entfernten Galaxienhaufen, vorwiegend über die Messung der Rotverschiebung möglich. Je nach verwendetem kosmologischen Modell kann daraus dann die Entfernung berechnet werden.

Für eine vereinfachte physikalische Beschreibung unseres Universums kann das idealisierte Standardmodell der Kosmologie verwendet werden. Die Stärke der Rotverschiebung wird in diesem Modell nur durch die kosmische Expansion festgelegt. Eine zusätzliche Rotverschiebung aufgrund einer Pekuliargeschwindigkeit, wie beispielsweise bei einer gravitativ gebundenen Haufengalaxie kann vernachlässigt werden, falls $z\gtrsim 0,2$ . Die globale Entwicklung des Universums wird im Standardmodell durch die Friedmann-Gleichungen beschrieben. Die Lichtausbreitung wird durch die zugrunde liegende raumzeitliche Geometrie und Dynamik wesentlich beeinflusst und es existiert deshalb kein eindeutiges Entfernungsmaß mehr. Dies widerspricht zwar der Alltagserfahrung in einem statischen euklidischen Raum, ist in einer dynamischen und gekrümmten Raumzeit wie bei unserem beobachtbaren Universum aber unvermeidbar.

Eine Veranschaulichung der verwendeten Entfernungsmaße kann teilweise dem Alltag auf der Erde entnommen werden. Beispielsweise kann bei bekannter Signalgeschwindigkeit aus der Laufzeit eines reflektierten Signals die Entfernung des angepeilten Objekts bestimmt werden. Dieses Prinzip wird bei Radarvermessungen oder dem sogenannten „Laser ranging“ verwendet. Andere Möglichkeiten bestehen darin, aus der scheinbaren Winkelgröße oder der scheinbaren Helligkeit eines Objekts dessen Entfernung abzuleiten. Hierfür müssen jedoch die wahre Größe beziehungsweise die wahre Helligkeit bekannt sein. Die unten beschriebenen Rechenmethoden können auch umgekehrt dazu benutzt werden, um die absolute Helligkeit oder die wahre Größe astronomischer Objekte zu bestimmen. Über die Laufzeit des Lichtes kann berechnet werden, wann das beobachtete Objekt das Licht ausgesendet hat.

In der Astrophysik und der Kosmologie werden die wichtigsten und am häufigsten verwendeten Entfernungsmaße Laufzeitentfernung, mitbewegte Entfernung, Winkeldurchmesserentfernung und Leuchtkraftentfernung genannt.

Laufzeitentfernung

Die Definition der Laufzeitentfernung (engl.: light travel time distance) basiert auf der Lichtlaufzeit zwischen zwei Ereignissen mit den Rotverschiebungen $z_{2}>z_{1}$ , gegeben durch

${\mathrm {d} }D_{\mathrm {prop} }(z_{1},z_{2})=-c\,{\mathrm {d} }t$

Substituiert man die kosmologische Zeit als Integrationsvariable durch die beobachtbare Rotverschiebung, so ergibt sich

${\mathrm {d} }D_{\mathrm {prop} }(z_{1},z_{2})=-c\,a/(a\,{\dot {a}})\,{\mathrm {d} }a=-c/(aH)\,{\mathrm {d} }a\,.$

Hierbei ist $a(t)$ der kosmologische Skalenfaktor, normiert auf den Wert 1 zur heutigen Zeit. Es gilt (siehe die relativistische Herleitung der kosmologischen Rotverschiebung)

$a={\frac {1}{1+z}}\;.$

Schreibt man dann die Hubble-Funktion $H$ für das Universum explizit aus, dann erhält man den geläufigen Ausdruck für die Laufzeitentfernung

$D_{\mathrm {prop} }(z_{1},z_{2})={\frac {c}{H_{0}}}\int _{a(z_{2})}^{a(z_{1})}\left[{\frac {\Omega _{r}}{a^{2}}}+{\frac {\Omega _{m}}{a}}+(1-\Omega _{r}-\Omega _{m}-\Omega _{\Lambda })+a^{2}\,\Omega _{\Lambda }\right]^{-1/2}\,{\mathrm {d} }a\;.$

Für ein flaches ( $1-\Omega _{m}-\Omega _{r}-\Omega _{\Lambda }=0$ ) und materiedominiertes ( $\Omega _{r}\approx 0$ ) Universum kann dieses Integral analytisch gelöst werden:

${\begin{aligned}D_{\mathrm {prop} }(z_{1},z_{2})&={\frac {2\,c}{3H_{0}{\sqrt {\Omega _{\Lambda }}}}}\;&&\left[\ln \left(a^{3/2}\Omega _{\Lambda }+{\sqrt {\Omega _{m}\Omega _{\Lambda }+a^{3}\Omega _{\Lambda }^{2}}}\right)\right]_{a(z_{2})}^{a(z_{1})}\\&={\frac {2}{\sqrt {3\Lambda }}}\;&&\left[\ln \left(a^{3/2}\Omega _{\Lambda }+{\sqrt {\Omega _{m}\Omega _{\Lambda }+a^{3}\Omega _{\Lambda }^{2}}}\right)\right]_{a(z_{2})}^{a(z_{1})}\,.\end{aligned}}$

$\Omega _{r}$ , $\Omega _{m}$ und $\Omega _{\Lambda }$ stellen hierbei die Strahlungsdichte-, Materiedichte- und den Vakuumenergiedichteparameter (kosmologische Konstante) dar. Nach Messungen mit dem Planck-Weltraumteleskop betragen diese $\Omega _{m}=0{,}315$ , $\Omega _{k}=-0{,}05$ und $\Omega _{\Lambda }=0{,}685$ . Die Hubble-Konstante beträgt $H_{0}=67{,}4$ km s⁻¹Mpc⁻¹, mit verschiedenen Abweichungen in Abhängigkeit vom verwendeten theoretischen Modell zur Auswertung der Messdaten.^[2]

Mitbewegte Entfernung

Die Evolution des Universums und seiner Horizonte in mitbewegten Koordinaten

In Analogie zur Laufzeitentfernung erhält man die mitbewegte Entfernung (engl.: comoving distance). Dies ist die Distanz zwischen der Quelle und dem Beobachter auf einer raumartigen Hyperfläche, definiert durch Ereignisse mit gleicher kosmologischer Zeit $t=t_{0}$ (heute). Ausgehend vom Linienelement und den Friedmann-Gleichungen ergibt sich

${\mathrm {d} }D_{\mathrm {com} }(z_{1},z_{2})={\mathrm {d} }w=-c/a\,{\mathrm {d} }t=-c/(a^{2}H)\,{\mathrm {d} }a\,,$

und damit

$D_{\mathrm {com} }(z_{1},z_{2})={\frac {c}{H_{0}}}\int _{a(z_{2})}^{a(z_{1})}\left[\Omega _{r}+a\,\Omega _{m}+a^{2}\,(1-\Omega _{m}-\Omega _{r}-\Omega _{\Lambda })+a^{4}\,\Omega _{\Lambda }\right]^{-1/2}\,{\mathrm {d} }a=w(z_{1},z_{2})\,.$

Der Unterschied zwischen Laufzeitentfernung und mitbewegter Entfernung besteht darin, dass Erstere eine Entfernung über Raum und Zeit hinweg ist. Die mitbewegte Entfernung ist hingegen die Distanz, die der Beobachter und das Objekt zum gleichen Weltalter zueinander aufweisen, das heißt eine Entfernung auf einer raumartigen Hyperfläche. In diesem Zustand kann der Beobachter das Objekt allerdings nicht sehen, da das Licht gerade eben vom Objekt zu ihm ausgesandt wurde.

Winkeldurchmesserentfernung

Die Evolution des Universums und seiner Horizonte in physikalischen Koordinaten

Die Winkeldurchmesserdistanz (engl.: angular size distance) ergibt sich aus einer bekannten Näherungsformel der Sinusfunktion. Für kleine Funktionsargumente gilt $\sin(x)\approx x$ . Diese Näherungsformel zeigt, warum die Winkeldurchmesserentfernung gemäß

$D_{\mathrm {A} }=d/\theta$

benutzt werden darf.^[3] Dabei ist $d$ die tatsächliche Größe des Objektes senkrecht zur Blickrichtung des Beobachters und $\theta$ die gemessene Winkelausdehnung des Objektes im Bogenmaß, unter dem das Objekt dem Beobachter erscheint.

Bei bekannter Rotverschiebung und bekanntem kosmologischen Modell gilt auch:

$D_{\mathrm {A} }(z_{1},z_{2})=a(z_{2})f_{K}\left(w(z_{1},z_{2})\right)\,.$

So kann dann von der Rotverschiebung auf die tatsächliche Größe eines Objektes geschlossen werden.

Unter Verwendung der mitbewegten Entfernung gilt:

$D_{\mathrm {A} }(z_{1},z_{2})=a(z_{2})f_{K}\left(D_{\mathrm {com} }(z_{1},z_{2})\right)\;,$

mit

$f_{K}(w)={\begin{cases}{\frac {1}{\sqrt {K}}}\;\sin({\sqrt {K}}w)&K>0\\w&K=0\;.\\{\frac {1}{\sqrt {-K}}}\;\sinh({\sqrt {-K}}w)&K<0\end{cases}}$

Die Funktion $f_{K}(w)$ unterscheidet zwischen dreidimensionalen raumartigen Hyperflächen konstanter Zeit $t$ mit positiver, verschwindender oder negativer Krümmung $K$ .

Leuchtkraftentfernung

Ebenso ergibt sich die Leuchtkraftentfernung (engl.: luminosity distance) aus der Analogie zur Euklidischen Geometrie. Berücksichtigt man die verspätete Ankunft der Photonen beim Beobachter durch die dazwischen liegende Ausdehnung des Universums, ihre Rotverschiebung sowie die Photonenzahlerhaltung, so erhält man

$D_{\mathrm {lum} }(z_{1},z_{2})={\frac {a(z_{1})^{2}}{a(z_{2})}}\,f_{K}\left(D_{\mathrm {com} }(z_{1},z_{2})\right)\;.$

Allgemeine Eigenschaften der verschiedenen Entfernungsdefinitionen

Durch die Vorfaktoren von $a$ und die Nichtlinearität von $f_{\mathrm {K} }$ , besitzen weder die Winkeldurchmesserentfernung noch die Leuchtkraftentfernung eine additive Eigenschaft. Betrachtet man zwei Objekte 1 und 3, mit einem dazwischen liegenden Objekt 2, dann ist die Entfernung zwischen 1 und 3 nicht gleich der Summe der Entfernungen zwischen Objekt 1 und 2, und Objekt 2 und 3:

$D(z_{1},z_{3})\neq D(z_{1},z_{2})+D(z_{2},z_{3})$

Die Laufzeitentfernung und die mitbewegte Entfernung hingegen sind additiv.

In einem flachen Universum gilt mit der konformen Zeit η:

$D_{\mathrm {com} }=D_{\mathrm {ang} }/a=D_{\mathrm {lum} }\cdot a=\Delta \eta \cdot c$

Zahlenbeispiele

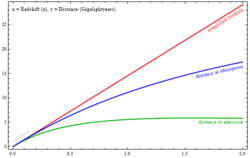
Für die folgenden Rotverschiebungen ergeben sich die verschiedenen Distanzen (in Milliarden Lichtjahren) zum Beobachter ( $z=0$ ):

$z$	0,1	0,5	01,0	03,0	006,0
Laufzeitentfernung $D_{\mathrm {prop} }$	1,280	4,970	07,600	11,190	012,370
Mitbewegte Entfernung $D_{\mathrm {com} }$	1,340	6,070	10,620	20,430	026,510
Winkeldurchmesserentfernung $D_{\mathrm {ang} }$	1,220	4,050	05,310	05,110	003,790
Leuchtkraftentfernung $D_{\mathrm {lum} }$	1,480	9,110	21,240	81,710	185,540

Hierbei fällt auf, dass die Winkeldurchmesserdistanz keine monotone Funktion der Rotverschiebung ist, sondern für $z=1{,}6$ ein Maximum aufweist, um danach wieder kleiner zu werden. Dies bedeutet, dass dasselbe Objekt für wachsende Rotverschiebungen immer kleiner erscheint, bei $z=1{,}6$ ein Minimum erreicht, und für größere Entfernungen dem Beobachter wieder größer erscheint.

Die Laufzeitentfernung nähert sich asymptotisch für unendlich große Rotverschiebungen einem konstanten Wert an. Die Leuchtkraftentfernung strebt für unendlich große Rotverschiebungen aber gegen unendlich. Das heißt, die scheinbare Helligkeit eines Objektes nimmt mit zunehmender Rotverschiebung sehr stark ab. In der Tat sinkt die Flächenhelligkeit mit $\propto (1+z)^{-4}$ .

Beispiele

Eine Galaxie habe die Rotverschiebung 0,5. Ihr Licht war demnach bis zum Beobachter 5,0 Milliarden Jahre unterwegs. Ihre Laufzeitdistanz beträgt damit 5,0 Milliarden Lichtjahre. Möchte man aus der scheinbaren Helligkeit der Galaxie (z. B. Magnitude = 22) auf ihre tatsächliche Helligkeit schließen, so muss die Leuchtkraftentfernung verwendet werden. Diese beträgt dann 9,1 Milliarden Lichtjahre. Ähnlich funktioniert die Größenbestimmung. Ermittelt ein Beobachter für die scheinbare Größe der Galaxie eine bestimmte Winkelausdehnung, so muss die Winkeldurchmesserdistanz verwendet werden, um ihre tatsächliche Größe zu bestimmen.

Die kosmische Hintergrundstrahlung hat heute eine gemessene Rotverschiebung von $z\approx 1089$ . Sie wurde also zu einem Zeitpunkt in der Vergangenheit ausgestrahlt, als das Universum rund $1/{\text{a}}=z+1=1090$ mal kleiner war als heute. Dieser Zeitpunkt fand dabei rund 380.000 Jahre nach dem Urknall statt. Die Oberfläche, von wo diese Strahlung emittiert oder zuletzt gestreut wurde, war zu diesem Zeitpunkt rund $D_{damals}$ = 40 Millionen Lichtjahre von uns entfernt und befindet sich heute in einem Abstand von rund $D_{heute}$ = 43,6 Milliarden Lichtjahre, also knapp vor dem Partikelhorizont.

Entfernung nach Rotverschiebung (Modell: ΛCDM, ΩR=0.0000548, ΩM=0.317, ΩΛ=1-ΩR-ΩM)

Siehe auch

Beobachtbares Universum

Weblinks

Literatur

C. Misner, K. S. Thorne, J. A. Wheeler: Gravitation. W. H. Freeman, San Francisco 1973, ISBN 0-7167-0344-0.
J. A. Peacock: Cosmological Physics. Cambridge University Press, 2001, ISBN 0-521-42270-1.
Torsten Fließbach: Allgemeine Relativitätstheorie. 4. Auflage. Elsevier – Spektrum Akademischer Verlag, 2003, ISBN 3-8274-1356-7.
Hans Stephani: Allgemeine Relativitätstheorie. 4. Auflage. Wiley-VCH, 1991, ISBN 3-326-00083-9.
Steven Weinberg: Gravitation and Cosmology. Principles and Applications of the General Theory of Relativity. New York 1972, ISBN 0-471-92567-5.

Einzelnachweise

↑ www.spektrum.de.
↑ Planck 2018 results. VI. Cosmological parameters Planck Collaboration, 09.08.2021, arxiv.org
↑ Tutorial Part 2 Ned Wright's cosmology calculator

Basierend auf einem Artikel in:

Wikipedia.de