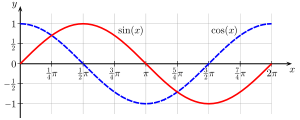
Sinus und Kosinus

Graphen der Sinusfunktion (rot) und der Kosinusfunktion (blau). Beide Funktionen haben eine Periode von $2\pi$ und nehmen Werte von −1 bis 1 an.

Sinus- und Kosinusfunktion (auch Cosinusfunktion) sind elementare mathematische Funktionen. Vor Tangens und Kotangens, Sekans und Kosekans bilden sie die wichtigsten trigonometrischen Funktionen. Sinus und Kosinus werden unter anderem in der Geometrie für Dreiecksberechnungen in der ebenen und sphärischen Trigonometrie benötigt. Auch in der Analysis sind sie wichtig.

Wellen wie Schallwellen, Wasserwellen und elektromagnetische Wellen lassen sich als aus Sinus- und Kosinuswellen zusammengesetzt beschreiben, sodass die Funktionen auch in der Physik als harmonische Schwingungen allgegenwärtig sind.

Herkunft des Namens

Die lateinische Bezeichnung Sinus „Bogen, Krümmung, Busen“ für diesen mathematischen Begriff wählte Gerhard von Cremona 1175 als Übersetzung der arabischen Bezeichnung gaib oder jiba (جيب) „Tasche, Kleiderfalte“, selbst entlehnt von Sanskrit jiva „Bogensehne“ indischer Mathematiker.

Die Bezeichnung „Cosinus“ ergibt sich aus complementi sinus, also Sinus des Komplementärwinkels. Diese Bezeichnung wurde zuerst in den umfangreichen trigonometrischen Tabellen verwendet, die von Georg von Peuerbach und seinem Schüler Regiomontanus erstellt wurden.

Geometrische Definition

Definition am rechtwinkligen Dreieck

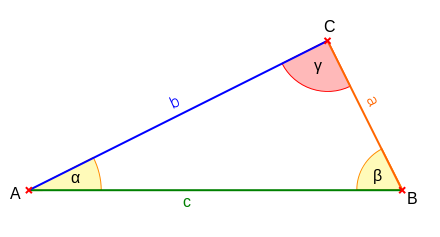
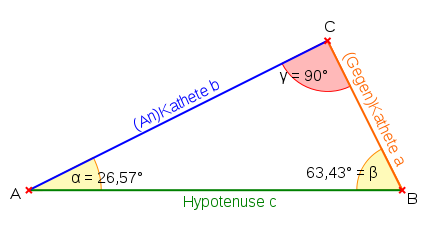
Dreieck mit den Punkten ABC und den gegenüberliegenden Seiten a,b,c.

Dreieck ABC mit einem rechten Winkel $\gamma$ in C. (Benennung von An- und Gegenkathete unter der Annahme, dass $\alpha$ der betrachtete Winkel ist.)

Alle ebenen, zueinander ähnlichen Dreiecke haben gleiche Winkel und gleiche Längenverhältnisse der Seiten.

Diese Eigenschaft wird benutzt, um Berechnungen am rechtwinkligen Dreieck durchzuführen. Sind nämlich die Längenverhältnisse im rechtwinkligen Dreieck bekannt, lassen sich die Maße von Winkeln und die Längen von Seiten berechnen. Deshalb haben die Längenverhältnisse im rechtwinkligen Dreieck auch besondere Namen.

Die Längenverhältnisse der drei Seiten im rechtwinkligen Dreieck sind nur vom Maß der beiden spitzen Winkel abhängig. Da aber das Maß eines dieser Winkel das Maß des anderen Winkels bereits festlegt (die Winkelsumme der beiden spitzen Winkel im rechtwinkligen Dreieck beträgt stets 90°), hängen die Längenverhältnisse im rechtwinkligen Dreieck nur vom Maß eines der beiden spitzen Winkel ab.

Deshalb werden die Längenverhältnisse in Abhängigkeit eines der beiden spitzen Winkel wie folgt definiert:

Der Sinus eines Winkels ist das Verhältnis der Länge der Gegenkathete (Kathete, die dem Winkel gegenüberliegt) zur Länge der Hypotenuse (Seite gegenüber dem rechten Winkel).

$\text{Sinus eines Winkels} = \frac{\text{Gegenkathete des Winkels}}{\text{Hypotenuse}}$

Der Kosinus ist das Verhältnis der Länge der Ankathete (das ist jene Kathete, die einen Schenkel des Winkels bildet) zur Länge der Hypotenuse.

$\text{Kosinus eines Winkels} = \frac{\text{Ankathete des Winkels}}{\text{Hypotenuse}}$

Bei den für Dreiecke üblichen Bezeichnungen der Größen (siehe Abbildung) gilt hier:

$\sin (\alpha) = \frac{a}{c} \quad \text{und} \quad \cos (\alpha) = \frac{b}{c}$

Da die Hypotenuse die längste Seite eines Dreiecks ist (denn sie liegt dem größten Winkel, also dem rechten Winkel, gegenüber), gelten die Ungleichungen $\sin\left(\alpha\right)\leq 1$ und $\cos\left(\alpha\right)\leq 1$ .

Wird statt von α von dem gegenüberliegenden Winkel β ausgegangen, so wechseln beide Katheten ihre Rolle, die Ankathete von α wird zur Gegenkathete von β und die Gegenkathete von α bildet nun die Ankathete von β und es gilt:

$\sin (\beta) = \frac{b}{c}$

$\cos (\beta) = \frac{a}{c}$

Da im rechtwinkligen Dreieck $\alpha + \beta = 90^\circ$ gilt, folgt:

$\cos (\alpha) = \sin(90^\circ - \alpha) = \sin(\beta)$

und

$\sin (\alpha) = \cos(90^\circ - \alpha) = \cos(\beta)$

Auf dieser Beziehung beruht auch die Bezeichnung Kosinus als Sinus des Komplementärwinkels.

Aus dem Satz des Pythagoras lässt sich die Beziehung („trigonometrischer Pythagoras“) ableiten:

$\sin^2 \left(\alpha\right) + \cos^2 \left(\alpha\right) = 1$

Im rechtwinkligen Dreieck sind Sinus und Kosinus nur für Winkel zwischen 0 und 90 Grad definiert. Für beliebige Winkel wird der Wert der Sinus-Funktion als -Koordinate und der der Kosinus-Funktion als -Koordinate eines Punktes am Einheitskreis (siehe unten) definiert. Hier ist es üblich, den Wert, auf den die Funktion angewendet wird (hier: den Winkel), als Argument zu bezeichnen. Dies betrifft insbesondere die Winkelfunktionen und die komplexe Exponentialfunktion (siehe unten).

Definition am Einheitskreis

Definition des Sinus und Kosinus am Einheitskreis

Trigonometrische Funktionen am Einheitskreis im ersten Quadranten

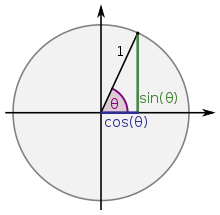
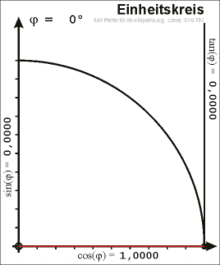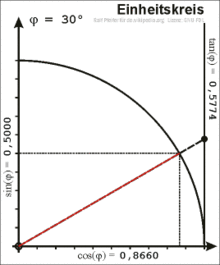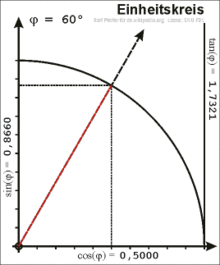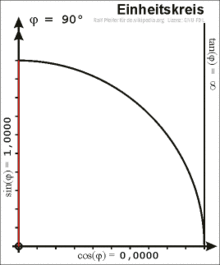
Im rechtwinkligen Dreieck ist der Winkel zwischen Hypotenuse und Kathete nur für Werte von 0 bis 90 Grad definiert. Für eine allgemeine Definition wird ein Punkt mit den Koordinaten (x,y) auf dem Einheitskreis betrachtet, hier gilt x^2+y^2=1 . Die positive -Achse schließt mit dem Ortsvektor von einen Winkel $\alpha$ ein. Der Koordinatenursprung (0,0) , der Punkt (x,0) auf der -Achse und der Punkt P(x,y) bilden ein rechtwinkliges Dreieck. Die Länge der Hypotenuse beträgt $\sqrt{x^2+y^2}=1$ . Die Ankathete des Winkels $\alpha$ ist die Strecke zwischen (0,0) und (x,0) und hat die Länge |x| . Es gilt:

$\cos(\alpha)=x$ .

Die Gegenkathete des Winkels $\alpha$ ist die Strecke zwischen (x,0) und (x,y) und hat die Länge $|y|$ . Somit ist:

$\sin(\alpha)=y$ .

Daraus folgt durch den Strahlensatz die Definition des Tangens:

$\tan\alpha =\frac{\sin\alpha}{\cos\alpha}$ .

Die -Koordinate eines Punktes im ersten Quadranten des Einheitskreises ist also der Sinus des Winkels zwischen seinem Ortsvektor und der -Achse, während die -Koordinate der Kosinus des Winkels ist. Die Fortsetzung über den ersten Quadranten hinaus ergibt eine Definition von Sinus und Kosinus für beliebige Winkel.

Die Umkehrung der Sinus-/Kosinusfunktion ist nicht eindeutig. Zu jeder Zahl zwischen −1 und 1 ( $-1<y<1$ ) gibt es schon zwischen 0° und 360° ( $0^{\circ }<\alpha \leq 360^{\circ }$ ) immer genau zwei Winkel. Symmetrien der Winkelfunktionen erkennt man an folgenden Beziehungen:

Punktsymmetrien:

$\sin(-\alpha)= -\sin(\alpha)$

und

$\cos(90^\circ+\alpha)=-\cos(90^\circ-\alpha)$ ,

Achsensymmetrien:

$\cos(-\alpha)= \cos(\alpha)$

und

$\sin(90^\circ+\alpha)=\sin(90^\circ-\alpha)$ .

Der Sinus ist also eine ungerade Funktion, der Kosinus eine gerade.

Sinus und Kosinus sind periodische Funktionen mit der Periode 360 Grad. (Man kann einen Winkel von beispielsweise 365° nicht von einem Winkel von 5° unterscheiden. Aber der eine beschreibt eine Drehbewegung von reichlich einer Umdrehung, der andere eine sehr kleine Drehbewegung ‒ nur eine zweiundsiebzigstel Umdrehung.) Also gilt auch

$\sin(\alpha +k\cdot 360^{\circ })=\sin(\alpha )$

sowie

$\cos(\alpha +k\cdot 360^{\circ })=\cos(\alpha )$ ,

wobei eine beliebige ganze Zahl ist. Es gibt also nicht nur die Symmetrien zu $\alpha=0^\circ$ (cos) bzw. $\alpha =90^{\circ }$ (sin) und zu (0,0) (sin) bzw. $(90^{\circ }|0)$ (cos), sondern unendlich viele Symmetrieachsen und Symmetriezentren für beide Funktionen.

Die Entstehung der Sinus- und Kosinusfunktion aus der Drehbewegung eines Winkelschenkels beginnend bei der -Achse veranschaulicht folgende Animation. Der Winkel wird im Bogenmaß gemessen. Ein Winkel von $360^{\circ }$ entspricht einem Bogenmaß von $2\pi$ .

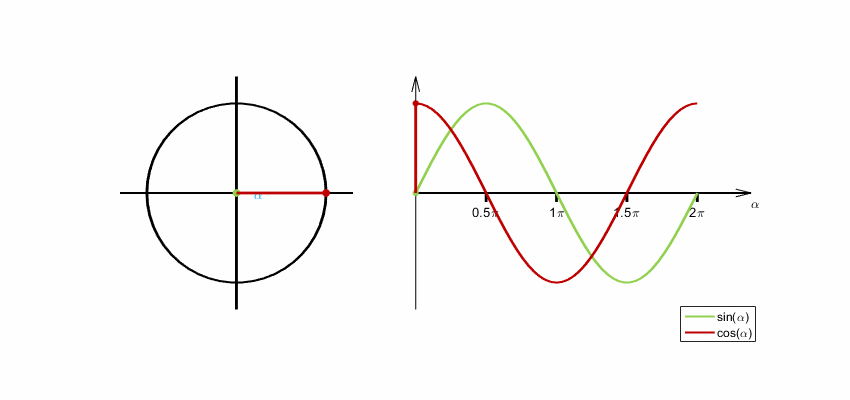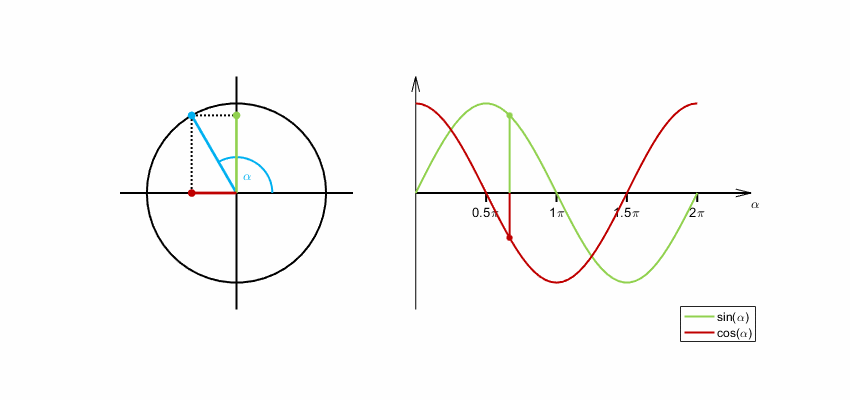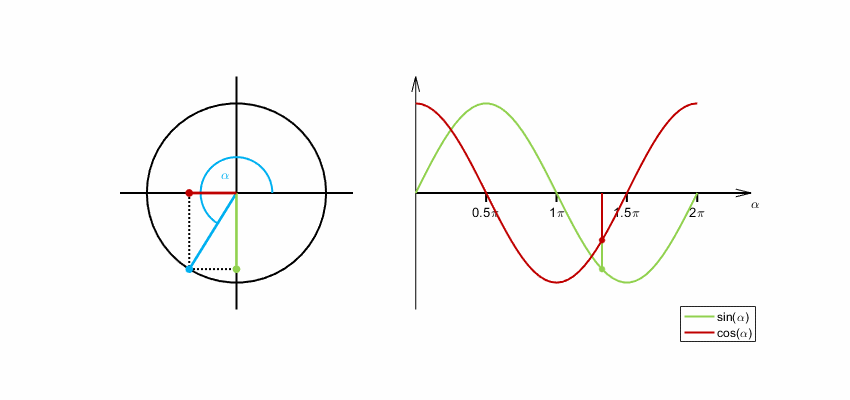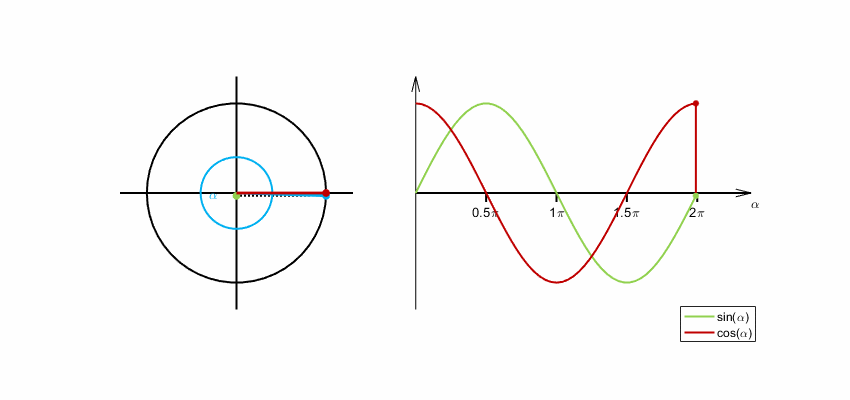
Animation zur Konstruktion der Sinus- und Kosinusfunktion

Analytische Definition

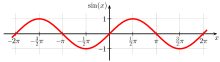
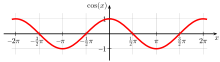
Graph der Sinusfunktion $x\mapsto \sin(x)$

Graph der Kosinusfunktion $x\mapsto \cos(x)$

Sinus und Kosinus können auch auf einer axiomatischen Basis behandelt werden; dieser formalere Zugang spielt auch in der Analysis eine Rolle. Die analytische Definition erlaubt zusätzlich die Erweiterung auf komplexe Argumente. Sinus und Kosinus als komplexwertige Funktion aufgefasst sind holomorph und surjektiv.

Motivation durch Taylorreihen

$\cos(x)$ zusammen mit den ersten Taylorpolynomen $p_{n}(x)=\sum _{k=0}^{n}(-1)^{k}{\frac {x^{2k}}{(2k)!}}$

Diese Animation illustriert die Definition der Sinusfunktion durch eine Reihe. Je höher die Zahl ist, desto mehr Summanden werden in der Reihendefinition verwendet. So ist bei

neben der Sinusfunktion zusätzlich das kubische Polynom $\sum _{k=0}^{2}{\tfrac {(-1)^{k}}{(2k+1)!}}x^{2k+1}=x-{\tfrac {x^{3}}{6}}$ eingezeichnet.

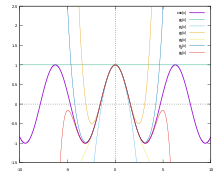
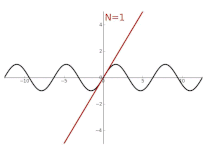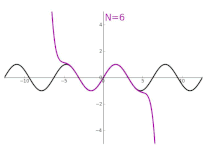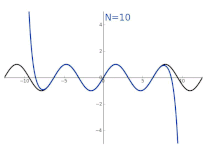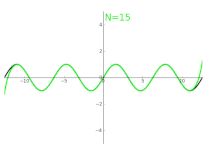
Durch den Übergang vom Winkelmaß zum Bogenmaß können Sinus und Cosinus als Funktionen von $\mathbb {R}$ nach $\mathbb {R}$ erklärt werden. Es kann nachgewiesen werden, dass sie beliebig oft differenzierbar sind. Für die Ableitungen im Nullpunkt gilt:

$\sin ^{(4n+k)}(0)=\left\{{\begin{matrix}0&{\text{wenn }}k=0\\1&{\text{wenn }}k=1\\0&{\text{wenn }}k=2\\-1&{\text{wenn }}k=3\end{matrix}}\right.\qquad \cos ^{(4n+k)}(0)=\left\{{\begin{matrix}1&{\text{wenn }}k=0\\0&{\text{wenn }}k=1\\-1&{\text{wenn }}k=2\\0&{\text{wenn }}k=3\end{matrix}}\right.$ .

Die Wahl des Bogenmaßes führt dazu, dass hier die Werte $\pm 1$ auftreten. Die sich daraus ergebenden Taylorreihen stellen die Funktionen $\sin(x)$ und $\cos(x)$ dar, das heißt:

$\sin (x) = \sum_{n=0}^\infty (-1)^n\frac{x^{2n+1}}{(2n+1)!} = \frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}\mp\dotsb$

$\cos (x) = \sum_{n=0}^\infty (-1)^n\frac{x^{2n}}{(2n)!} = \frac{x^0}{0!}-\frac{x^2}{2!}+\frac{x^4}{4!}\mp\dotsb$

Reihenentwicklung in der Analysis

In der Analysis geht man von einer Reihenentwicklung aus und leitet umgekehrt daraus alles her, indem die Funktionen sin und cos durch die oben angegebenen Potenzreihen erklärt werden. Mit dem Quotientenkriterium lässt sich zeigen, dass diese Potenzreihen für jede komplexe Zahl absolut und in jeder beschränkten Teilmenge der komplexen Zahlen gleichmäßig konvergieren. Diese unendlichen Reihen verallgemeinern die Definition des Sinus und des Kosinus von reellen auf komplexe Argumente. Auch $\pi$ wird dort üblicherweise nicht geometrisch, sondern beispielsweise über die cos-Reihe und die Beziehung $\cos\left(\tfrac{\pi}{2}\right)=0$ als das Doppelte der kleinsten positiven Nullstelle der Kosinusfunktion definiert. Damit ist eine präzise analytische Definition von $\pi$ gegeben.

Für kleine Werte zeigen diese Reihen ein sehr gutes Konvergenzverhalten. Zur numerischen Berechnung lassen sich daher die Periodizität und Symmetrie der Funktionen ausnutzen und der -Wert bis auf den Bereich $-\pi/4$ bis $\pi/4$ reduzieren. Danach sind für eine geforderte Genauigkeit nur noch wenige Glieder der Reihe zu berechnen. Das Taylorpolynom der Kosinusfunktion bis zur vierten Potenz z.B. hat im Intervall $[-\pi/4, \pi/4]$ einen relativen Fehler von unter 0,05 %. Im Artikel Taylor-Formel sind einige dieser so genannten Taylorpolynome grafisch dargestellt und eine Näherungsformel mit Genauigkeitsangabe angegeben. Zu beachten ist allerdings, dass die Teilsummen der Taylorpolynome nicht die bestmögliche numerische Approximation darstellen.

Beziehung zur Exponentialfunktion

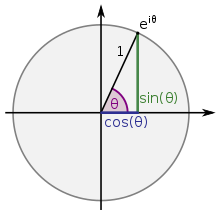
Der Realteil von $\mathrm {e} ^{\mathrm {i} \theta }$ ist $\cos \theta$ und der Imaginärteil ist $\sin \theta$ .

Die trigonometrischen Funktionen sind eng mit der Exponentialfunktion verbunden, wie folgende Rechnung zeigt:

$\begin{align} \mathrm{e}^{\mathrm{i}x} &= \sum^{\infty}_{k=0}\frac{(\mathrm{i}x)^k}{k!} = \sum^{\infty}_{l=0}\frac{(\mathrm{i}x)^{2l}}{(2l)!} + \sum^{\infty}_{l=0}\frac{(\mathrm{i}x)^{2l+1}}{(2l+1)!}\\ &=\underbrace{\sum^{\infty}_{l=0}(-1)^l \frac{x^{2l}}{(2l)!}}_{\cos x} + \mathrm{i} \underbrace{\sum^{\infty}_{l=0} (-1)^l \frac{x^{2l+1}}{(2l+1)!}}_{\sin x}\\ &= \cos x + \mathrm{i} \sin x \end{align}$

Dabei wurde verwendet $\mathrm{i}^{2l} = (\mathrm{i}^2)^l = (-1)^l\,$ sowie $\mathrm{i}^{2l+1}= \mathrm{i}\cdot \mathrm{i}^{2l} = \mathrm{i}(-1)^l$

Beziehung zwischen Sinus, Kosinus und Exponentialfunktion

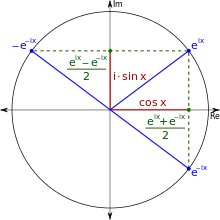
Somit ergibt sich die sogenannte Eulerformel

$\mathrm {e} ^{\mathrm {i} x}=\cos x+\mathrm {i} \cdot \sin x$ .

Für eine reelle Zahl ist also $\cos(x)$ der Realteil und $\sin(x)$ der Imaginärteil der komplexen Zahl $\mathrm{e}^{\mathrm{i}\,x}$ .

Durch Ersetzung von durch ergibt sich:

$\mathrm {e} ^{-\mathrm {i} x}=\cos x-\mathrm {i} \cdot \sin x$ .

Diese und die vorangegangenen Gleichungen lassen sich nach den trigonometrischen Funktionen auflösen. Es folgt:

$\sin x={\frac {1}{2\mathrm {i} }}\left(\mathrm {e} ^{\mathrm {i} x}-\mathrm {e} ^{-\mathrm {i} x}\right)$

und

$\cos x={\frac {1}{2}}\left(\mathrm {e} ^{\mathrm {i} x}+\mathrm {e} ^{-\mathrm {i} x}\right)$ .

Diese Gleichung gilt nicht nur für reelle Argumente, sondern für beliebige komplexe Zahlen. Somit ergibt sich eine alternative Definition für die Sinus- und Kosinusfunktion. Durch Einsetzen der Exponentialreihe leiten sich die oben vorgestellten Potenzreihen ab.

Ausgehend von dieser Definition lassen sich viele Eigenschaften, wie zum Beispiel die Additionstheoreme des Sinus und Kosinus, nachweisen.

Definition über analytische Berechnung der Bogenlänge

Die Definition des Sinus und Kosinus als Potenzreihe liefert einen sehr bequemen Zugang, da die Differenzierbarkeit durch die Definition als konvergente Potenzreihe automatisch gegeben ist. Die Eulerformel ist ebenfalls eine einfache Konsequenz aus den Reihendefinitionen, da sich die Reihen für $\cos\,$ und $i\,\sin$ ganz offenbar zur Exponentialfunktion zusammenfügen, wie oben gezeigt wurde. Durch Betrachtung der Funktion $x\mapsto e^{i x}$ , die das Intervall $[0,2\pi]$ auf die Kreislinie abbildet, ergibt sich die Beziehung zur Geometrie, denn $\cos(x)$ und $\sin(x)$ sind nichts weiter als der Real- bzw. Imaginärteil von $e^{ix}$ , das heißt die Projektion dieses Punktes auf die Koordinatenachsen.

Neben $x\mapsto e^{ix}$ gibt es auch andere sinnvolle Parametrisierungen des Einheitskreises, etwa

$\gamma(t) = \left(\frac{1-t^2}{1+t^2},\frac{2t}{1+t^2}\right),\quad -\infty<t<\infty.$

Geht man von dieser Formel aus, erhält man einen alternativen Zugang. Die Länge dieser Kurve wird auch als Bogenlänge bezeichnet und berechnet sich als

$s(t) = \int_0^t |\dot\gamma(\tau)|\,\mathrm d\tau =\int_0^t\frac{2\,\mathrm d\tau}{\tau^2+1}.$

Wie leicht zu zeigen ist, ist s(t) ungerade, stetig, streng monoton wachsend und beschränkt. Da die gesamte Bogenlänge dem Kreisumfang entspricht, folgt, dass das Supremum von s(t) gleich $\pi$ ist; $\pi$ wird bei dieser Vorgangsweise analytisch als Supremum von s(t) definiert.

Die Funktion

$s(t)\colon\mathbb R\to(-\pi,\pi)$

ist auch differenzierbar:

$\frac{\mathrm d s}{\mathrm d t} = \frac{2}{1+t^2}$ .

Weil sie stetig und streng monoton wachsend ist, ist sie auch invertierbar, und für die Umkehrfunktion

$t(s)\colon(-\pi,\pi) \to \mathbb R$

gilt

$\frac{\mathrm d t}{\mathrm d s} = \frac{1+t^2(s)}{2}$ .

Mit Hilfe dieser Umkehrfunktion t(s) lassen sich nun Sinus und Kosinus als - und -Komponente von $\gamma$ analytisch definieren:

$\sin s := \frac{2t(s)}{1+t^2(s)}$

sowie

$\cos s := \frac{1-t^2(s)}{1+t^2(s)}$ .

Bei dieser Definition des Sinus und Kosinus über die analytische Berechnung der Bogenlänge werden die geometrischen Begriffe sauber formalisiert. Sie hat allerdings den Nachteil, dass im didaktischen Aufbau der Analysis der Begriff der Bogenlänge erst sehr spät formal eingeführt wird und daher Sinus und Kosinus erst relativ spät verwendet werden können.

Definition als Lösung einer Funktionalgleichung

Ein anderer analytischer Zugang ist, Sinus und Kosinus als Lösung einer Funktionalgleichung zu definieren, die im Wesentlichen aus den Additionstheoremen besteht: Gesucht ist ein Paar stetiger Funktionen $\sin, \cos\colon\R\to\R$ , das für alle $x,y\in\R$ die Gleichungen

$\sin(x+y)=\sin(x)\cos(y)+\cos(x)\sin(y)$ und

$\cos(x+y)=\cos(x)\cos(y)-\sin(x)\sin(y)$

erfüllt. Die Lösung $\sin$ definiert dann den Sinus, die Lösung $\cos$ den Kosinus. Um Eindeutigkeit zu erreichen, sind einige Zusatzbedingungen zu erfüllen. In Heuser, Lehrbuch der Analysis, Teil 1 wird zusätzlich gefordert, dass

$\sin(x)$ eine ungerade Funktion,

$\cos(x)$ eine gerade Funktion,

$\lim_{x\to 0}\frac{\sin(x)}{x}=1$ und

$\cos(0)=1$

ist. Bei diesem Zugang wird offensichtlich die Differenzierbarkeit des Sinus in 0 vorausgesetzt; $\pi$ wird in weiterer Folge analytisch als das doppelte der kleinsten positiven Nullstelle des Kosinus definiert. Verwendet man den Zugang von Leopold Vietoris^[1] und berechnet die Ableitung des Sinus aus den Additionstheoremen, so ist es zweckmäßiger, $\pi$ auf geeignete Weise analytisch (beispielsweise als Hälfte des Grenzwerts des Umfangs des dem Einheitskreis eingeschriebenen $2^{n}$ -Ecks) zu definieren und dann die Differenzierbarkeit der Lösung dieser Funktionalgleichung zu beweisen. Als Zusatzbedingung zu den Additionstheoremen fordert man dann beispielsweise

$\sin\left(\frac{\pi}{2}\right)=1$ ,

$\cos\left(\frac{\pi}{2}\right)=0$ , und

$\cos\left(\frac{\pi}{2n}\right)\ne 0$ für alle $n\in\N\backslash\lbrace 1 \rbrace$ .

Unter den gewählten Voraussetzungen ist die Eindeutigkeit der Lösung der Funktionalgleichung relativ einfach zu zeigen; die geometrisch definierten Funktionen Sinus und Kosinus lösen auch die Funktionalgleichung. Die Existenz einer Lösung lässt sich analytisch beispielsweise durch die Taylorreihen von Sinus und Kosinus oder eine andere der oben verwendeten analytischen Darstellungen von Sinus und Kosinus die Funktionalgleichung nachweisen und tatsächlich lösen.

Produktentwicklung

$\sin(x) = x \prod_{k=1}^\infty \left( 1 - \frac{x^2}{k^2\pi^2} \right)$

$\cos(x) = \prod_{k=1}^\infty \left( 1 - \frac{4x^2}{(2k-1)^2\pi^2} \right)$

$\sin(x)=\prod _{n=-\infty }^{\infty }\left({\frac {x+n\pi }{{\frac {\pi }{2}}+n\pi }}\right)$

$\cos(x)=\prod _{n=-\infty }^{\infty }\left({\frac {x+n\pi +{\frac {\pi }{2}}}{{\frac {\pi }{2}}+n\pi }}\right)$

$x\;$ ist dabei im Bogenmaß anzugeben.

Wertebereich und spezielle Funktionswerte

Zusammenhang zwischen Sinus und Kosinus

$\sin(\alpha)=-\cos\left(\alpha + 90^\circ \right)=\cos\left(\alpha-90^\circ\right)$ (Gradmaß)

$\sin(\alpha)=-\cos\left(\alpha + \pi/2 \right)=\cos\left(\alpha - \pi/2\right)$ (Bogenmaß)

$\sin^2\left(\alpha\right)+\cos^2(\alpha)=1$ („trigonometrischer Pythagoras“)

Insbesondere folgt daraus $|{\sin\alpha}|\leq 1$ und $|{\cos\alpha}|\leq 1$ . Diese Ungleichungen gelten aber nur für reelle Argumente $\alpha$ ; für komplexe Argumente können Sinus und Kosinus beliebige Werte annehmen.

Verlauf des Sinus in den vier Quadranten

In den vier Quadranten ist der Verlauf der Sinusfunktion folgendermaßen:

Quadrant	Gradmaß	Bogenmaß	Bildmenge	Monotonie	Konvexität	Punkttyp
	$0^\circ$	0	0			Nullstelle, Wendepunkt
1. Quadrant	$0^\circ<x<90^\circ$	$0<x< \pi/2$	positiv: $0<\sin x<1$	steigend	konkav
	$90^{\circ }$	$\pi/2$	1			Maximum
2. Quadrant	$90^\circ<x<180^\circ$	$\pi/2<x<\pi$	positiv: $0<\sin x<1$	fallend	konkav
	$180^{\circ }$	$\pi$	0			Nullstelle, Wendepunkt
3. Quadrant	$180^\circ<x<270^\circ$	$\pi<x<3\pi/2$	negativ: $-1<\sin x<0$	fallend	konvex
	$270^\circ$	$3\pi/2$				Minimum
4. Quadrant	$270^\circ<x<360^\circ$	$3\pi/2<x<2\pi$	negativ: $-1<\sin x<0$	steigend	konvex

Für Argumente außerhalb dieses Bereiches ergibt sich der Wert des Sinus daraus, dass der Sinus periodisch mit der Periode 360° (bzw. 2π rad) ist, d.h. $\sin(\alpha + 360^\circ) = \sin(\alpha)$ . Außerdem gilt $\sin(\alpha + 180^\circ) = -\sin(\alpha)$ , $\sin(90^{\circ }+\alpha )=\sin(90^{\circ }-\alpha )$ , $\sin(180^{\circ }-\alpha )=\sin(\alpha )$ etc.

Verlauf des Kosinus in den vier Quadranten

Der Kosinus stellt einen um 90° (bzw. π/2 rad) phasenverschobenen Sinus dar und es gilt $\cos(\alpha)=\sin(\alpha+90^\circ)$ .

In den vier Quadranten ist der Verlauf der Kosinusfunktion daher folgendermaßen:

Quadrant	Gradmaß	Bogenmaß	Bildmenge	Monotonie	Konvexität	Punkttyp
	$0^\circ$	0	1			Maximum
1. Quadrant	$0^\circ<x<90^\circ$	$0<x<\pi/2$	positiv: $0<\cos x<1$	fallend	konkav
	$90^{\circ }$	$\pi/2$	0			Nullstelle, Wendepunkt
2. Quadrant	$90^\circ<x<180^\circ$	$\pi/2<x<\pi$	negativ: $-1<\cos x<0$	fallend	konvex
	$180^{\circ }$	$\pi$				Minimum
3. Quadrant	$180^\circ<x<270^\circ$	$\pi<x<3\pi/2$	negativ: $-1<\cos x<0$	steigend	konvex
	$270^\circ$	$3\pi/2$	$0$			Nullstelle, Wendepunkt
4. Quadrant	$270^\circ<x<360^\circ$	$3\pi/2<x<2\pi$	positiv: $0<\cos x<1$	steigend	konkav

Für Argumente außerhalb dieses Bereiches lässt sich der Wert des Kosinus – so wie der des Sinus – periodisch mit der Periode 360° (bzw. 2π rad) bestimmen, d.h. $\cos(\alpha + 360^\circ) = \cos(\alpha)$ . Außerdem gilt $\cos(\alpha + 180^\circ) = -\cos(\alpha)$ .

Komplexes Argument

Graph der komplexen Sinusfunktion

Graph der komplexen Kosinusfunktion

Farbfunktion, die für die beiden obigen Bilder verwendet wurde.

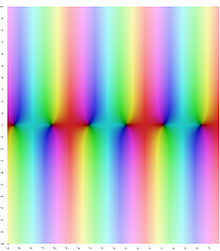
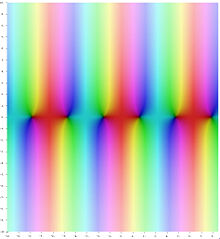
Für komplexe Argumente kann man Sinus und Kosinus entweder über die Reihenentwicklung oder über die Formeln

$\sin z={\frac {1}{2\mathrm {i} }}\left(\mathrm {e} ^{\mathrm {i} z}-\mathrm {e} ^{-\mathrm {i} z}\right)$

$\cos z={\frac {1}{2}}\left(\mathrm {e} ^{\mathrm {i} z}+\mathrm {e} ^{-\mathrm {i} z}\right)$

definieren.

Für komplexe Argumente $z=x+\mathrm{i}\cdot{y}$ gilt

$\sin\left(z\right)=\sin\left(x+\mathrm{i}\cdot{y}\right)=\sin\left(x\right)\cosh\left(y\right)+\mathrm{i}\cos\left(x\right)\sinh\left(y\right)$

und

$\cos\left(z\right)=\cos\left(x+\mathrm{i}\cdot{y}\right)=\cos\left(x\right)\cosh\left(y\right)-\mathrm{i}\sin\left(x\right)\sinh\left(y\right)$ ,

was aus den Additionstheoremen und den Zusammenhängen $\sin\left(\mathrm{i}\cdot{y}\right)=\mathrm{i}\cdot{\sinh\left(y\right)}$ sowie $\cos\left(\mathrm{i}\cdot{y}\right)=\cosh\left(y\right)$ hergeleitet werden kann, wobei $\sinh$ und $\cosh$ die Hyperbelfunktionen Sinus und Cosinus Hyperbolicus bezeichnen.

Sinus und Kosinus sind für reelle Argumente auf Werte aus dem Intervall [-1, 1] beschränkt; im Definitionsbereich der komplexen Zahlen $\mathbb {C}$ sind sie dagegen unbeschränkt, was aus dem Satz von Liouville folgt. Sinus und Kosinus können für komplexe Argumente sogar beliebige reelle oder komplexe Werte annehmen.

Zum Beispiel ist

$\cos\left(\mathrm{i}\right)=\cosh\left(1\right)=\frac{e^1+e^{-1}}{2}\approx 1{,}54.$

Für reelle nimmt $\cos(x)$ diesen Wert aber nie an.

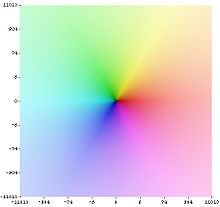
In den Bildern auf der rechten Seite gibt die Farbe den Winkel des Arguments an, die Farbintensität den Betrag, wobei volle Intensität für kleine Werte steht und bei großen Beträgen ein Übergang zu weiß stattfindet. Die genaue Zuordnung ergibt sich aus nebenstehendem Bild, das jeder komplexen Zahl eine Farbe und eine Intensität zuordnet. An den Bildern zu Sinus und Kosinus ist erkennbar, dass auch im Komplexen Periodizität in -Richtung vorliegt (nicht aber in -Richtung) und dass Sinus und Kosinus durch eine Verschiebung um $\pi/2$ auseinander hervorgehen.

Wichtige Funktionswerte

Da Sinus und Kosinus periodische Funktionen mit der Periode $2\pi$ (entspricht im Gradmaß $360^{\circ }$ ) sind, reicht es, die Funktionswerte der beiden trigonometrischen Funktionen für den Bereich $[0,2\pi]$ (entspricht dem Bereich $0^\circ$ bis $360^{\circ }$ ) zu kennen. Funktionswerte außerhalb dieses Bereichs können also aufgrund der Periodizität durch den Zusammenhang

$\sin(x) = \sin(x + 2k \pi)\quad \text{und}\quad \cos(x) = \cos(x + 2k \pi)$

bestimmt werden. In Gradmaß lautet der Zusammenhang analog

$\sin(x) = \sin(x + k \cdot 360^\circ)\quad \text{und}\quad \cos(x) = \cos(x + k \cdot 360^\circ)\,.$

Hierbei bezeichnet $k \in \Z$ eine ganze Zahl. Die folgende Tabelle listet die wichtigen Funktionswerte der beiden trigonometrischen Funktionen in einer leicht zu merkenden Reihe auf.

Winkel (Grad)	Bogenmaß	Sinus	Kosinus
$0^\circ$	$0$	$\frac12\sqrt0 = 0$	$\frac12\sqrt4 = 1$
$30^{\circ }$	$\frac{\pi}{6}$	$\frac12\sqrt1 = \frac12$	$\frac12\sqrt3$
$45^{\circ }$	${\frac {\pi }{4}}$	$\frac12\sqrt2=\frac{1}{\sqrt2}$	$\frac12\sqrt2=\frac{1}{\sqrt2}$
$60^{\circ }$	$\frac{\pi}{3}$	$\frac12\sqrt3$	$\frac12\sqrt1 = \frac12$
$90^{\circ }$	$\frac{\pi}{2}$	$\frac12\sqrt4 = 1$	$\frac12\sqrt0 = 0$

Weitere wichtige Werte sind:

Winkel (Grad)	Bogenmaß	Sinus	Kosinus
$15^\circ$	$\tfrac{\pi}{12}$	$\tfrac14(\sqrt{6}-\sqrt{2})$	$\tfrac14(\sqrt{6}+\sqrt{2})$
$18^\circ$	$\tfrac{\pi}{10}$	$\tfrac{1}{4}\left(\sqrt{5}-1\right)$	$\tfrac{1}{4}\sqrt{10+2\sqrt{5}}$
$36^{\circ }$	${\tfrac {\pi }{5}}$	$\tfrac{1}{4} \sqrt{10- 2\sqrt{5}}$	$\tfrac{1}{4} \left (1+ \sqrt{5} \right)$
$54^\circ$	${\tfrac {3\pi }{10}}$	$\tfrac{1}{4} \left (1+ \sqrt{5} \right)$	$\tfrac{1}{4} \sqrt{10- 2\sqrt{5}}$
$72^{\circ }$	$\tfrac{2\pi}{5}$	$\tfrac{1}{4} \sqrt{10+ 2\sqrt{5}}$	$\tfrac{1}{4} \left (\sqrt{5}-1 \right)$
$75^\circ$	$\tfrac{5\pi}{12}$	$\tfrac14(\sqrt{6}+\sqrt{2})$	$\tfrac14(\sqrt{6}-\sqrt{2})$
$180^{\circ }$	$\pi$
$270^\circ$	$\frac{3\pi}{2}$
$360^{\circ }$	$2\pi$	$0$

Beweisskizzen:

$\cos(45^{\circ })=\sin(45^{\circ })={\tfrac {1}{2}}{\sqrt {2}}$ , weil das rechtwinklige Dreieck im Einheitskreis (mit der Hypotenuse 1) dann gleichschenklig ist, und nach Pythagoras gilt $x^{2}+x^{2}=1^{2}\Rightarrow x={\tfrac {1}{2}}{\sqrt {2}}$ .
$\cos(60^{\circ })=\sin(30^{\circ })={\tfrac {1}{2}}$ , weil das rechtwinklige Dreieck im Einheitskreis (mit der Hypotenuse 1) gespiegelt an der -Achse dann gleichseitig ist (mit Seitenlänge 1), und somit die Gegenkathete (Sinus) die halbe Seitenlänge beträgt.
$\cos(30^{\circ })=\sin(60^{\circ })={\tfrac {1}{2}}{\sqrt {3}}$ , weil für das rechtwinklige Dreieck im Einheitskreis (mit der Hypotenuse 1) wegen $\sin(30^{\circ })={\tfrac {1}{2}}$ für den Cosinus nach Pythagoras gilt $x^{2}+\left({\tfrac {1}{2}}\right)^{2}=1^{2}\ \Rightarrow \ x^{2}={\tfrac {3}{4}}\ \Rightarrow \ x={\tfrac {1}{2}}{\sqrt {3}}$ .
$\cos(72^{\circ })=\sin(18^{\circ })={\tfrac {1}{4}}({\sqrt {5}}-1)$ , weil im Pentagramm das Inverse des Goldenen Schnitts auftritt, wobei der halbierte Winkel in den Spitzen gleich 18° ist.
$\cos(36^{\circ })=\sin(54^{\circ })={\tfrac {1}{4}}(1+{\sqrt {5}})$ , weil im regelmäßigen Fünfeck der Goldene Schnitt auftritt, wobei der halbierte Innenwinkel gleich 54° ist.
$\cos(75^{\circ })=\sin(15^{\circ })$ und IMG class="text" style="width: 19.44ex; height: 2.84ex; vertical-align: -0.83ex;" alt="{\displaystyle \cos(15^{\circ })=\sin(75^{\circ })}" src="/svg/6c74e0bf01c6d08229f3d8fd99cc445bc93d5aac.svg"> lassen sich mit Hilfe der Halbwinkelformeln für Sinus und Kosinus herleiten.

Weitere mit Quadratwurzeln angebbare Funktionswerte

Über die Berechnung der fünften Einheitswurzeln mittels einer quadratischen Gleichung ergibt sich

$\sin(18^\circ)=\cos(72^\circ)=\frac{\sqrt{5}-1}{4}$ .

Mit Hilfe der Additionstheoreme lassen sich viele weitere solche Ausdrücke berechnen wie beispielsweise die Seitenlänge eines regulären Fünfecks über

$\cos(54^\circ)=\sin(2\cdot18^\circ)=\frac{1}{2}\sqrt{\frac{5-\sqrt{5}}{2}}$

und $\sin(15^\circ)$ , woraus folgt

$\frac{\sqrt{3}}{2}=\cos(30^\circ)=\cos^2(15^\circ)-\sin^2(15^\circ)=1-2\sin^2(15^\circ)$ .

Aus $\sin(18^\circ)$ und $\sin(15^\circ)$ lassen sich dann z.B. $\sin(3^\circ)$ und dann rekursiv auch alle $\sin(k \cdot 3^\circ)$ , $k\in\Z\;$ ermitteln.

Generell gilt, dass $\sin\alpha\;$ und $\cos\alpha\;$ genau dann explizit mit den vier Grundrechenarten und Quadratwurzeln darstellbar sind, wenn der Winkel $\alpha \;$ mit Zirkel und Lineal konstruierbar ist, insbesondere also wenn $\alpha \;$ von der Gestalt

$\alpha=k\frac{360^\circ}{2^np_1\dots p_r}$

ist, wobei $k\in\Z\;$ , $n\in\N_0\;$ und die $p_i\;$ für $i=1,\dots,r\;$ Fermatsche Primzahlen sind. In obigem Beispiel von $\alpha=3^\circ$ ist $k=1\;$ und der Nenner gleich $120=2^3\cdot 3\cdot 5.$

Fixpunkte

Fixpunkt der Kosinusfunktion

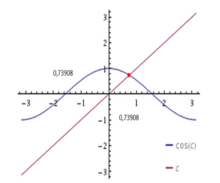
Die Fixpunktgleichung $\sin(x)=x$ besitzt

als einzige reelle Lösung.

Die Gleichung $\cos(x)=x$ hat als einzige reelle Lösung

$x=0{,}73908513321516\ldots$ (Folge A003957 in OEIS).

Die Lösung dieser Fixpunktgleichung wurde bereits 1748 von Leonhard Euler untersucht. Sie ist ein einfaches Beispiel für einen nichttrivialen global attraktiven Fixpunkt, das heißt die Fixpunktiteration $x_{{n+1}}=\cos(x_{n})$ konvergiert für jeden Startwert $x_{0}$ gegen die Lösung. Mit dem Satz von Lindemann-Weierstraß kann nachgewiesen werden, dass es sich dabei um eine transzendente Zahl handelt. Diese mathematische Konstante wird im englischen Sprachraum auch als Dottie number bezeichnet und mit dem armenischen Buchstaben ա (Ayb) abgekürzt.

Berechnung

Zur Berechnung von Sinus und Cosinus gibt es mehrere Verfahren. Die Wahl des Berechnungsverfahrens richtet sich nach Kriterien wie Genauigkeit, Geschwindigkeit der Berechnung und Leistungsfähigkeit der verwendeten Hardware wie zum Beispiel Mikrocontroller:

Tabellierung aller benötigten Funktionswerte
Tabellierung von Funktionswerten zusammen mit Interpolationsverfahren
Berechnung mit dem CORDIC-Algorithmus
Verwendung der Taylor-Reihe
schnelle, aber grob genäherte Abschätzung mit Hilfe der Zwölftel-Regel

Die Tabellierung aller Werte ist angezeigt bei geschwindigkeitskritischen Echtzeitsystemen, wenn diese nur eine recht kleine Winkelauflösung benötigen. CORDIC ist i.d.R. effizienter umsetzbar als die Taylor-Reihe und zudem besser konditioniert.

Umkehrfunktion

→ Hauptartikel: Arkussinus und Arkuskosinus

Da sich zu einem gegebenen Wert $\sin\alpha\in [-1,1]$ ein passender Winkel im ersten oder vierten Quadranten und zu einem gegebenen Wert $\cos\alpha\in [-1,1]$ ein passender Winkel im ersten oder zweiten Quadranten konstruieren lässt, folgt aus diesen geometrischen Überlegungen, dass die Funktionen

$\begin{align} \sin \colon &[-90^\circ, 90^\circ]&\to[-1,1]\\ \cos \colon &[0^\circ, 180^\circ]&\to[-1,1] \end{align}$

Umkehrfunktionen besitzen. Die Umkehrfunktionen

$\begin{align} \arcsin\colon [-1,1] &\to [-90^\circ, 90^\circ] \\ \arccos\colon [-1,1] &\to [0^\circ, 180^\circ] \end{align}$

werden Arkussinus bzw. Arkuskosinus genannt. Der Name rührt daher, dass sich deren Wert nicht nur als Winkel, sondern auch als Länge eines Kreisbogens (Arcus bedeutet Bogen) interpretieren lässt.

In der Analysis ist die Verwendung des Bogenmaßes erforderlich, da die Winkelfunktionen dort für das Bogenmaß definiert sind. Die Sinusfunktion

$\sin \colon \left[-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right]\to [-1,1]$

und die Kosinusfunktion

$\cos\colon [0, \pi]\to[-1,1]$

sind auf den angegebenen Definitionsbereichen streng monoton, surjektiv und daher invertierbar. Die Umkehrfunktionen sind

$\begin{align} \arcsin\colon [-1,1] &\to \left[-\tfrac{\pi}{2}, \tfrac{\pi}{2} \right] \\ \arccos\colon [-1,1] &\to \left[0, \pi \right] \end{align}$

Eine andere Interpretation des Wertes als doppelter Flächeninhalt des dazugehörigen Kreissektors am Einheitskreis ist ebenfalls möglich; diese Interpretation ist insbesondere für die Analogie zwischen Kreis- und Hyperbelfunktionen nützlich.

Zusammenhang mit dem Skalarprodukt

Der Kosinus steht in enger Beziehung mit dem Standardskalarprodukt zweier Vektoren $\vec{a}=\left( a_1, a_2, \dots, a_n \right)$ und $\vec{b}=\left( b_1, b_2, \dots, b_n \right)$ :

$\vec{a}\cdot \vec{b} = |\vec{a} | \, | \vec{b} | \, \cos \measuredangle (\vec{a},\vec{b})= {a_1}{b_1}+{a_2}{b_2}+\dots + {a_n}{b_n}$

das Skalarprodukt ist also die Länge der Vektoren multipliziert mit dem Kosinus des eingeschlossenen Winkels. In endlichdimensionalen Räumen lässt sich diese Beziehung aus dem Kosinussatz ableiten. In abstrakten Skalarprodukträumen wird über diese Beziehung der Winkel zwischen Vektoren definiert.

Zusammenhang mit dem Kreuzprodukt

→ Hauptartikel: Kreuzprodukt

Der Sinus steht in enger Beziehung mit dem Kreuzprodukt zweier dreidimensionaler Vektoren ${\vec {a}}$ und $\vec{b}$ :

$|\vec{a}\times\vec{b}|=|\vec{a}| \, | \vec{b} | \, \sin \measuredangle (\vec{a},\vec{b})$

Additionstheoreme

→ Hauptartikel: Additionstheoreme (Trigonometrie)

Die Additionstheoreme für Sinus und Kosinus lauten

$\sin ( x \pm y ) = \sin x \; \cos y \pm \cos x \; \sin y$

$\cos ( x \pm y ) = \cos x \; \cos y \mp \sin x \; \sin y$

Aus den Additionstheoremen folgt insbesondere für doppelte Winkel

$\sin(2x)=2\sin x\;\cos x$

$\cos(2x)=\cos ^{2}x-\sin ^{2}x=1-2\sin ^{2}x=2\cos ^{2}x-1$

Orthogonale Zerlegung

Die harmonische Schwingung

$a(x)={\sqrt {2}}A\sin(x+\varphi _{a})$

wird durch

$a(x)={\frac {1}{B^{2}}}{\overline {a(x)b(x)}}\cdot b(x)+{\frac {1}{B^{2}}}{\overline {a(x)b'(x)}}\cdot b'(x)$

in orthogonale Komponenten zur Basis der harmonischen Schwingung

$b(x)={\sqrt {2}}B\sin(x+\varphi _{b})$

zerlegt. und sind Effektivwerte, $\varphi _{a}$ und $\varphi _{b}$ Nullphasenwinkel. Ihre Differenz

$\varphi =\varphi _{a}-\varphi _{b}$

heißt Phasenverschiebungswinkel. Die Ableitung der Basisfunktion

$b'(x)={\frac {{\text{d}}b(x)}{{\text{d}}x}}$

läuft b(x) um eine Viertelperiode voraus. Die in den Zerlegungskoeffizienten enthaltenen Gleichwerte folgen aus einer modifizierten Fourier-Analyse, bei der nicht die Sinus- und Kosinusfunktion, sondern b(x) und $b'(x)$ als Basis dienen. Durch Einsetzen der harmonischen Ansätze ergibt sich schließlich

$a(x)={\frac {A}{B}}\cos \varphi \cdot b(x)+{\frac {A}{B}}\sin \varphi \cdot b'(x)$ .

Die Zerlegung gilt auch bei Ansatz von a(x) und b(x) mit der Kosinusfunktion.

Ableitung, Integration und Krümmung von Sinus und Kosinus

Ableitung

Wird $x\;$ im Bogenmaß angegeben, so gilt für die Ableitung der Sinusfunktion

$\sin^\prime(x) = \cos(x)$

Aus $\cos(x)=\sin\left(\tfrac{\pi}{2}-x\right)$ und der Kettenregel erhält man die Ableitung des Kosinus:

$\cos^\prime(x) = -\sin(x)$

und daraus schließlich auch alle höheren Ableitungen von Sinus und Kosinus

$\sin ^{(4n+k)}(x)=\left\{{\begin{matrix}\sin(x),&{\text{wenn }}k=0\\\cos(x),&{\text{wenn }}k=1\\-\sin(x),&{\text{wenn }}k=2\\-\cos(x),&{\text{wenn }}k=3\end{matrix}}\right.$

$\cos ^{(4n+k)}(x)=\left\{{\begin{matrix}\cos(x),&{\text{wenn }}k=0\\-\sin(x),&{\text{wenn }}k=1\\-\cos(x),&{\text{wenn }}k=2\\\sin(x),&{\text{wenn }}k=3\end{matrix}}\right.$

Wird der Winkel $\alpha$ in Grad gemessen, so kommt nach der Kettenregel bei jeder Ableitung ein Faktor ${\tfrac {\pi }{180^{\circ }}}$ dazu, also beispielsweise $\sin ^{\prime }(\alpha )={\tfrac {\pi }{180^{\circ }}}\cos(\alpha )$ . Um diese störenden Faktoren zu vermeiden, wird in der Analysis der Winkel ausschließlich im Bogenmaß angegeben.

Stammfunktion

Aus den Ergebnissen über die Ableitung ergibt sich unmittelbar die Stammfunktion von Sinus und Kosinus im Bogenmaß:

$\int \sin(x)\,{\mathrm {d}}x=-\cos(x)+C$

$\int \cos(x)\,{\mathrm {d}}x=\sin(x)+C$

Krümmung

Die Krümmung des Graphen wird mit Hilfe der Formel

$\kappa (x)={\frac {f''(x)}{\left(1+f'(x)^{2}\right)^{3/2}}}$

berechnet. Für $f(x)=\sin(x)$ erhält man damit die Krümmungsfunktion

$\kappa (x)=-{\frac {\sin(x)}{\left(1+\cos ^{2}(x)\right)^{3/2}}}$ .

und für $f(x)=\cos(x)$ entsprechend

$\kappa (x)=-{\frac {\cos(x)}{\left(1+\sin ^{2}(x)\right)^{3/2}}}$ .

An den Wendepunkten ist die Krümmung gleich null. Dort hat die Krümmungsfunktion einen Vorzeichenwechsel. An der Stelle des Maximums ist die Krümmung gleich −1 und an der Stelle des Minimums gleich 1. Der Krümmungskreis hat an den Extrempunktem also jeweils den Radius 1.

Anwendungen

Geometrische Anwendungen

Skizze zum Beispiel

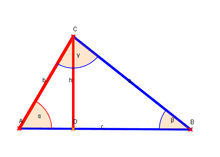
Mit der Definition des Sinus können auch im nicht rechtwinkligen Dreieck Größen, speziell die Höhen, berechnet werden; ein Beispiel ist die Berechnung von $h_{c}$ im Dreieck ABC bei gegebener Länge a=5{,}4 und Winkel $\beta=42^\circ$ :

$\begin{align} \frac{h_c}{a} &= \sin(\beta)\\ h_c &= a\cdot \sin(\beta)\\ h_c &= 5{,}4 \cdot \sin (42^\circ) \approx 3{,}613 \end{align}$

Andere wichtige Anwendungen sind der Sinussatz und der Kosinussatz.

Fourierreihen

Im Hilbertraum $L^{2}[-\pi ,\pi ]$ der auf dem Intervall $[-\pi,\pi]$ bezüglich des Lebesgue-Maßes quadratisch integrierbaren Funktionen bilden die Funktionen

$1,\cos nx,\sin nx\quad n=1,2,\dotsc$

ein vollständiges Orthogonalsystem, das sogenannte trigonometrische System. Daher lassen sich alle Funktionen $f\in L^2[-\pi,\pi]$ als Fourierreihe

$S_n(x)=\frac{a_0}{2} + \sum_{k=1}^n (a_k\cos kx + b_k \sin kx)$

darstellen, wobei die Funktionenfolge $S_{n}(x)$ in der L²-Norm gegen f(x) konvergiert.

Anwendungen in der Informatik

In der Informatik wird zur Erstellung von Audiodateien (zum Beispiel im Audioformat MP3), digitalen Bildern im Grafikformat JPEG, Videodateien (zum Beispiel im Containerformat MP4 oder WebM) die diskrete Kosinustransformation oder die modifizierte diskrete Kosinustransformation verwendet. Zum Abspielen oder Anzeigen solcher Dateien wird die inverse diskrete Kosinustransformation, also die Umkehrfunktion verwendet. Bei der digitalen Verarbeitung von akustischen und optischen Signalen wird unter anderem die Schnelle Fourier-Transformation verwendet.

Physikalische Anwendungen

In der Physik werden Sinus- und Kosinusfunktion zur Beschreibung von Schwingungen verwendet. Insbesondere lassen sich durch die oben erwähnten Fourierreihen beliebige periodische Signale als Summe von Sinus- und Kosinusfunktionen darstellen, siehe Fourieranalyse.

Elektrotechnische Anwendungen

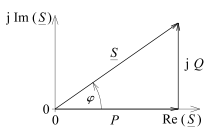
Leistungszeigerdiagramm und Phasenverschiebungswinkel bei sinusförmigen Spannungen und Strömen in der komplexen Ebene

In der Elektrotechnik sind häufig elektrische Stromstärke und Spannung sinusförmig. Wenn sie sich um einen Phasenverschiebungswinkel $\varphi$ unterscheiden, dann unterscheidet sich die aus Stromstärke und Spannung gebildete Scheinleistung von der Wirkleistung .

$S=U\cdot I\quad ;\quad P=U\cdot I\cdot \cos \varphi$

Bei nicht sinusförmigen Größen (z.B. bei einem Netzteil mit herkömmlichem Brückengleichrichter am Eingang) entstehen Oberschwingungen, bei denen sich kein einheitlicher Phasenverschiebungswinkel angeben lässt. Dann lässt sich zwar noch ein Leistungsfaktor angeben

$\text{Leistungsfaktor }\lambda = \frac{|P|}S\quad,$

dieser Leistungsfaktor $\lambda$ darf aber mit $\cos(\varphi )$ nicht verwechselt werden.

Siehe auch

Literatur

Harro Heuser: Lehrbuch der Analysis – Teil 1. 6. Auflage. Teubner, 1989.

Anmerkungen

↑ Leopold Vietoris: Vom Grenzwert $\lim_{x\to 0}\tfrac{\sin x}{x}$ . In: Elemente der Mathematik. Band 12, 1957.

Basierend auf einem Artikel in:

Wikipedia.de