Geschwindigkeitsgesetz

Geschwindigkeitsgesetze oder Geschwindigkeitsgleichungen (englisch: rate laws) stellen in der chemischen Kinetik den Zusammenhang zwischen der Reaktionsgeschwindigkeit $r$ einerseits und Gehaltsgrößen von Ausgangsstoffen chemischer Reaktionen sowie konstanten Parametern andererseits her.^[1] Als Gehaltsgrößen werden üblicherweise Konzentrationen, teilweise jedoch auch andere Maße für die Verfügbarkeit von Ausgangsstoffen, so etwa Partialdrücke oder relative Bedeckungen der Oberflächen von heterogenen Katalysatoren,^[2]^[3] verwendet. Bei den konstanten Parametern kann es sich um Geschwindigkeitskonstanten oder Halbwertszeiten sowie partielle Reaktionsordnungen (siehe unten) der Ausgangsstoffe handeln.

Geschwindigkeitsgesetze 0. bis 2. Ordnung

Allgemeine Formulierung

Häufig ist die Reaktionsgeschwindigkeit $r$ einer chemischen Reaktion proportional zu Produkten von Potenzfunktionen der Konzentrationen der Ausgangsstoffe. Sind an einer chemischen Reaktion $N$ Ausgangsstoffe $\mathrm {Z_{j}}$ mit den Konzentrationen $\mathrm {[Z_{j}]}$ beteiligt, erhält man mit der Geschwindigkeitskonstante $k$ Geschwindigkeitsgesetze der allgemeinen Form:

$r=k\prod _{j=1}^{N}[\mathrm {Z_{j}} ]^{z_{j}}$

Die Exponenten $z_{j}$ bezeichnet man als partielle Reaktionsordnungen in Bezug auf die Ausgangsstoffe $\mathrm {Z_{j}}$ . Die Gesamtreaktionsordnung $n$ der betrachteten chemischen Reaktion ist gleich der Summe der partiellen Reaktionsordnungen $z_{j}$ :

${\textstyle n=\sum \limits _{j=1}^{N}z_{j}}$

0. Ordnung

Geschwindigkeitsgesetze 0. Ordnung beschreiben chemische Reaktionen mit einer Gesamtreaktionsordnung $n$ von null. Da dann üblicherweise auch die partiellen Reaktionsordnungen $z_{j}$ in Bezug auf die Ausgangsstoffe $\mathrm {Z_{j}}$ gleich null und die Potenzfunktionen $\mathrm {[Z_{j}]} ^{z_{j}}$ der Konzentrationen der Ausgangsstoffe gleich eins werden, wird die Reaktionsgeschwindigkeit $r$ gleich der Geschwindigkeitskonstante $k$ . Geschwindigkeitsgesetze 0. Ordnung nehmen folglich folgende Form an:^[4]

$r=k\cdot [\mathrm {A} ]^{0}=k$

Die Reaktionsgeschwindigkeit $r$ ist somit unabhängig von den Konzentrationen $\mathrm {[Z_{j}]}$ der Ausgangsstoffe. Geschwindigkeitsgesetze 0. Ordnung können beispielsweise bei heterogenen Reaktionen auftreten.^[3]^[4]^[5] Weiterhin weisen viele enzymatische Katalysen eine Kinetik 0. Ordnung auf, sofern das Substrat in großem Überschuss vorliegt.^[5]^[6]

1. Ordnung

Geschwindigkeitsgesetze 1. Ordnung beschreiben chemische Reaktionen mit einer Gesamtreaktionsordnung $n$ von eins. Üblicherweise ist die partielle Reaktionsordnung $a$ in Bezug auf einen Ausgangsstoff ${\ce {A}}$ gleich eins, während alle anderen partiellen Reaktionsordnungen $z_{j}$ in Bezug auf eventuell vorhandene weitere Ausgangsstoffe $\mathrm {Z_{j}}$ gleich null sind. Entsprechend werden die Potenzfunktionen $\mathrm {[Z_{j}]} ^{z_{j}}$ der Konzentrationen eventuell vorhandener weiterer Ausgangsstoffe $\mathrm {Z_{j}}$ gleich eins, und die Potenzfunktion $\mathrm {[A]} ^{a}$ der Konzentration des Ausgangsstoffes ${\ce {A}}$ gleich der Konzentration ${\ce {[A]}}$ . Dann hängt die Reaktionsgeschwindigkeit $r$ vom Produkt der Geschwindigkeitskonstante $k$ mit ${\ce {[A]}}$ ab, so dass Geschwindigkeitsgesetze 1. Ordnung folgende Form annehmen:

$r=k\cdot [\mathrm {A} ]$

Typischerweise sind unimolekulare Zerfallsreaktionen mit einer Molekularität von eins Reaktionen 1. Ordnung. Ein Beispiel hierfür sind radioaktive Zerfallsreaktionen. Ebenfalls erster Ordnung sind chemische Reaktionen, die als langsamste Elementarreaktion und damit als geschwindigkeitsbestimmenden Schritt einen unimolekularen Zerfall umfassen. Beispiele hierfür sind Eliminierungen und nukleophile Substitutionen 1. Ordnung.

2. Ordnung

Geschwindigkeitsgesetze 2. Ordnung beschreiben die Kinetik von Elementarreaktionen mit einer Molekularität von zwei, die einen bimolekularen Stoß umfassen. Umfasst die betrachtete Reaktion einen Stoß zweier gleichartiger Teilchen ${\ce {A}}$ , wird die Reaktionsgleichung:

${\ce {A + A -> Produkte}}$

Die Reaktionsgeschwindigkeit ist dann proportional zum Quadrat ${\ce {[A]^2}}$ der Konzentration ${\ce {[A]}}$ des Ausgangsstoffes ${\ce {A}}$ . Die partielle Reaktionsordnung in Bezug auf ${\ce {A}}$ ist gleich der Gesamtreaktionsordnung und damit gleich zwei. Das Geschwindigkeitsgesetz wird:

$r=k\cdot [\mathrm {A} ]^{2}$

Ein derartiges Szenario kann beispielsweise bei Reaktionen auftreten, die nach dem Lindemann-Mechanismus ablaufen.

Weiterhin beschreiben Geschwindigkeitsgesetze 2. Ordnung die Kinetik von Elementarreaktionen mit einer Molekularität von zwei, die einen bimolekularen Stoß zweier verschiedenartiger Teilchen ${\ce {A}}$ und ${\ce {B}}$ umfassen. Die Reaktionsgleichung lautet dann:

${\ce {A + B -> Produkte}}$

Die Reaktionsgeschwindigkeit ist dann proportional zum Produkt der Konzentrationen ${\ce {[A]}}$ und ${\ce {[B]}}$ der Ausgangsstoffe ${\ce {A}}$ und ${\ce {B}}$ . Die partiellen Reaktionsordnungen in Bezug auf die Ausgangsstoffe ${\ce {A}}$ und ${\ce {B}}$ sind jeweils eins. Das Geschwindigkeitsgesetz wird entsprechend:

$r=k\cdot [\mathrm {A} ]\cdot [\mathrm {B} ]$

Beispiele hierfür sind bimolekulare konzertierte Elementarreaktionen, wie Eliminierungen und nukleophile Substitutionen 2. Ordnung.

Pseudo-Reaktionsordnungen

Betrachtet wird beispielhaft eine Elementarreaktion 2. Ordnung, an der Ausgangsstoff ${\ce {A}}$ mit der Konzentration ${\ce {[A]}}$ sowie Ausgangsstoff ${\ce {B}}$ mit der Konzentration ${\ce {[B]}}$ teilnehmen. Wenn die partiellen Reaktionsordnungen in Bezug auf ${\ce {A}}$ und ${\ce {B}}$ jeweils eins sind, lautet das Geschwindigkeitsgesetz:

$r=k[{\ce {A}}][{\ce {B}}]$

Die Elementarreaktion kann nun eine Pseudo-Ordnung aufweisen, die den Reaktionsmechanismus und die Molekularität nicht widerspiegelt, weil ${\ce {[B]}}$ im Verlauf der Reaktion (näherungsweise) konstant bleibt. Dies kann der Fall sein, wenn es sich bei ${\ce {B}}$ um einen regenerierenden Katalysator handelt, wenn ${\ce {B}}$ in einem offenen Reaktionssystem kontinuierlich nachgeliefert wird oder wenn ${\ce {[B] >> [A]}}$ ist. In derartigen Fällen können die Geschwindigkeitskonstante $k$ und ${\ce {[B]}}$ zu einer Pseudo-Konstante $k'$ zusammengefasst werden:

$k'=k[{\ce {B}}]$

Damit vereinfacht sich das Geschwindigkeitsgesetz 2. Ordnung zu einem Geschwindigkeitsgesetz, in dem die partielle Reaktionsordnung von ${\ce {A}}$ , die gleich eins ist, anscheinend zur Gesamtreaktionsordnung wird:

$r=k[{\ce {A}}][{\ce {B}}]=k'[{\ce {A}}]$

Anscheinende Gesamtreaktionsordnungen von Elementarreaktionen, die sich von der Molekularität letzterer unterscheiden, bezeichnet man als Pseudo-Reaktionsordnungen.^[7] Im obigen Beispiel ist das Geschwindigkeitsgesetz $r=k'[{\ce {A}}]$ pseudo-erster Ordnung.

Ein Beispiel für eine Reaktion pseudo-erster Ordnung ist Hydrolyse von Estern in wässeriger Lösung:

${\ce {CH3COOCH3 + H2O -> CH3COOH + CH3OH}}$

Die partiellen Reaktionsordnungen in Bezug auf ${\ce {CH3COOCH3}}$ und ${\ce {H2O}}$ sind jeweils eins, die Gesamtreaktionsordnung ist zwei. Das Geschwindigkeitsgesetz der Reaktion lautet entsprechend:

${\ce {{\it {r}}\;=\;{\it {k}}\cdot [CH3COOCH3]\cdot [H2O]}}$

Da jedoch der Ausgangsstoff Wasser gleichzeitig als Lösungsmittel fungiert, gilt:

${\ce {[CH3COOCH3] << [H2O]}}$

Somit kann ${\ce {[H2O]}}$ als konstant angesehen werden. Mit ${\ce {{\it {k}}'\;=\;{\it {k}}\cdot [H2O]}}$ erhält man ein Geschwindigkeitsgesetz mit der Pseudo-Reaktionsordnung eins:

${\ce {{\it {r}}\;=\;{\it {k}}'\cdot [CH3COOCH3]}}$

Ebenso ist die Rohrzuckerinversion, die Reaktion von Saccharose (Rohrzucker) und Wasser zu D-Glucose und D-Fructose (Invertzucker), eigentlich eine Reaktion 2. Ordnung, wobei die partiellen Reaktionsordnungen in Bezug auf die Ausgangsstoffe jeweils eins sind:

${\ce {C12H22O11 + H2O -> C6H12O6 + C6H12O6}}$

Da das Lösungsmittel Wasser in großem Überschuss vorliegt, findet man auch für diese Reaktion die pseudo-Reaktionsordnung eins.^[7]

Bestimmung partieller Reaktionsordnungen

Integrationsmethode

Zeitgesetze geben die Konzentration $[\mathrm {A} ](t)$ eines an einer Reaktion beteiligten Eduktes ${\ce {A}}$ als Funktion der Reaktionsdauer $t$ an. In einigen Fällen lassen sich Zeitgesetze in Form von Geradengleichungen angeben (siehe Kinetik (Chemie)). Ist die partielle Reaktionsordnung in Bezug auf ${\ce {A}}$ gleich 0, muss die Auftragung von $[{\text{A}}](t)$ gegen $t$ eine Gerade ergeben. Ist die partielle Reaktionsordnung in Bezug auf ${\ce {A}}$ gleich 1, muss die Auftragung von $\ln \left([{\text{A}}](t)/[{\text{A}}]_{0}\right)$ gegen $t$ eine Gerade ergeben. Ist die partielle Reaktionsordnung in Bezug auf ${\ce {A}}$ gleich 2, muss die Auftragung von $1/[{\text{A}}](t)$ gegen $t$ eine Gerade ergeben. Sofern aus einer dieser Auftragungen mit experimentell erhaltenen Wertepaaren eine Regressionsgerade mit einem zufriedenstellenden Bestimmtheitsmaß resultiert, spricht dies dafür, dass die partielle Reaktionsordnung von ${\ce {A}}$ den entsprechenden Wert besitzt.^[8]^[9]^[10]

Methode der Anfangsgeschwindigkeit

Der natürliche Logarithmus eines Geschwindigkeitsgesetzes, in dem die Reaktionsgeschwindigkeit gleich einem Produkt von Potenzfunktionen der Konzentrationen der Edukte gesetzt wird, ist (da Einheiten nicht logarithmierbar sind, würde man vor dem Logarithmieren beide Seiten des Geschwindigkeitsgesetzes formal durch die Einheit der Reaktionsgeschwindigkeit teilen):

$\ln r=\ln k+\sum \limits _{j=1}^{N}\ln[{\ce {Z}}_{j}]^{z_{j}}=\ln k+\sum \limits _{j=1}^{N}(z_{j}\cdot \ln[{\ce {Z}}_{j}])$

Im Falle einer Reaktion 2. Ordnung erhält man mit $a$ und $b$ als den partiellen Reaktionsordnungen der Edukte ${\ce {A}}$ und ${\ce {B}}$ entsprechend:

$\ln r=\ln k+a\ln[{\ce {A}}]+b\ln[{\ce {B}}]$

Zur Abschätzung der partiellen Reaktionsordnung $a$ von Ausgangsstoff ${\ce {A}}$ führt man mehrere Versuchsansätze mit verschiedenen Anfangskonzentrationen ${\ce {[A]_0}}$ von ${\ce {A}}$ durch. Die Anfangskonzentration ${\ce {[B]_0}}$ von Ausgangsstoff ${\ce {B}}$ hält man hingegen konstant. Man misst dann die Anfangsreaktionsgeschwindigkeit $r_{0}$ unmittelbar nach Start der Reaktion. Für kleine Reaktionsdauern $t$ gilt näherungsweise

$[\mathrm {A} ](t)\approx [\mathrm {A} ]_{0}$

sowie

$[\mathrm {B} ](t)\approx [\mathrm {B} ]_{0}={\text{Konstante}}$ .

Dann erhält man:

$\ln r_{0}\approx a\ln[{\ce {A}}]_{0}+{\textrm {Konstante}}$

Der Logarithmus der Anfangsgeschwindigkeit $\ln r_{0}$ als Funktion von ${\ce {ln [A]_0}}$ sollte dann eine Gerade ergeben, deren Steigung $a$ ist. Ein Nachteil dieser Methode ist, dass zur Bestimmung von ${\ce {r_0}}$ relativ kleine Änderungen von ${\ce {[A]}}$ gemessen werden müssen, so dass erhebliche Anstrengungen in die Minimierung von Messfehlern investiert werden müssen.^[10]^[11]

Halbwertszeitverfahren

Partielle Reaktionsordnungen in Bezug auf einen Ausgangsstoff ${\ce {A}}$ lassen sich mittels der Halbwertszeiten $t_{1/2}$ ermitteln, also derjenigen Reaktionsdauer, innerhalb derer die Anfangskonzentration ${\ce {[A]_0}}$ von ${\ce {A}}$ auf ihren halben Wert $[\mathrm {A} ](t_{1/2})=1/2\cdot [\mathrm {A} ]_{0}$ gefallen ist. Der stöchiometrische Koeffizient des Ausgangsstoffes ${\ce {A}}$ sei, konventionsgemäß mit negativem Vorzeichen, $\nu _{\mathrm {A} }$ . Zur Bestimmung der partiellen Reaktionsordnung von ${\ce {A}}$ wird $t_{1/2}$ für verschiedene Werte von ${\ce {[A]_0}}$ ermittelt.^[8]^[12]

Ist die partielle Reaktionsordnung von ${\ce {A}}$ gleich 0, wird:

$t_{1/2}=-{\frac {[{\text{A}}]_{0}}{2\nu _{\text{A}}k}}$

Es muss dann also gelten: $t_{1/2}\sim [\mathrm {A} ]_{0}$

Ist die partielle Reaktionsordnung von ${\ce {A}}$ gleich 1, gilt:

$t_{1/2}=-{\frac {\ln 2}{\nu _{\mathrm {A} }k}}$

Dann ist $t_{1/2}$ unabhängig von $[\mathrm {A} ]_{0}$ .

Ist die partielle Reaktionsordnung von ${\ce {A}}$ gleich 2, gilt:

$t_{1/2}=-{\frac {1}{\nu _{\text{A}}k[{\text{A}}]_{0}}}$

Logarithmieren ergibt:

$\ln t_{1/2}=\ln \left(-{\frac {1}{\nu _{\text{A}}k}}\right)+\ln {\frac {1}{[{\text{A}}]_{0}}}$

Es muss dann also gelten:

$\ln t_{1/2}\sim \ln {\frac {1}{[{\text{A}}]_{0}}}$

Überschuss-Methode

Nach Wilhelm Ostwald kann die partielle Reaktionsordnung ${\ce {A}}$ abgeschätzt werden, wenn alle anderen Ausgangsstoffe in so großem Überschuss vorliegen, dass deren Konzentration als konstant betrachtet werden kann. Dies kann beispielsweise der Fall sein, wenn ${\ce {A}}$ ein gelöster Stoff ist und ein zweiter Ausgangsstoff ${\ce {B}}$ gleichzeitig als Lösungsmittel fungiert. Die Konzentration $[\mathrm {A} ](t)$ von ${\ce {A}}$ wird für verschiedene Reaktionsdauern $t$ gemessen. Für eine Reaktion ${\ce {A + B -> Produkte}}$ wird das Geschwindigkeitsgesetz mit $a$ und $b$ als partiellen Reaktionsordnungen von ${\ce {A}}$ und ${\ce {B}}$ :^[13]

$r=k\cdot [{\rm {A}}]^{a}\cdot [{\rm {B}}]^{b}$

Da ${\ce {[B]}}$ und folglich ${\ce {[B]^{b}}}$ als konstant betrachtet werden können, wird mit $k'=k\cdot [{\rm {B}}]^{b}$ :

$r=k'\cdot [{\rm {A}}]^{a}$

Dieser Ausdruck wird logarithmiert. Die partielle Reaktionsordnung $a$ von ${\ce {A}}$ lässt sich als Steigung der so erhaltenen Gerade ermitteln:

$\ln r=\ln k'+a\cdot \ln[{\rm {A}}]$

Komplexe Geschwindigkeitsgesetze

Hintergrund

Viele chemische Bruttoreaktionen sind durch komplexe Reaktionsmechanismen gekennzeichnet, die eine Reihe von konsekutiv oder parallel ablaufenden Elementarreaktionen umfassen, die in die Bruttogeschwindigkeitsgesetze der Gesamtreaktionen eingehen. Sofern die Rückreaktionen von Elementarreaktionen nennenswerte Geschwindigkeiten aufweisen, müssen diese bei der Aufstellung von Bruttogeschwindigkeitsgesetzen für Gesamtreaktionen berücksichtigt werden. Weiterhin können Szenarios existieren, in denen Konkurrenzreaktionen in die Geschwindigkeitsgesetze der Reaktionen von Interesse eingehen. Hieraus resultieren oft komplexe Geschwindigkeitsgesetze, die Brüche und/oder mehrere Geschwindigkeitskonstanten und/oder gemischte Reaktionsordnungen in Bezug auf bestimmte Ausgangsstoffe und/oder gebrochene Reaktionsordnungen in Bezug auf bestimmte Ausgangsstoffe enthalten. Teilweise lassen sich Geschwindigkeitsgesetze durch Näherungen vereinfachen. Beispielsweise lässt sich die Kinetik von zusammengesetzten Reaktionen, in deren Verlauf mehrere konsekutive Elementarreaktionen auftreten, häufig in zufriedenstellender Weise durch die Kinetik einer langsam ablaufenden Elementarreaktion, die als geschwindigkeitsbestimmender Schritt bezeichnet wird, annähern. Treten im Verlauf von zusammengesetzten Reaktionen reaktive Intermediate auf, kann die Beschreibung der Reaktionskinetik durch das Bodensteinsche Quasistationaritätsprinzip vereinfacht werden. Andererseits kann aus Geschwindigkeitsgesetzen nicht unmittelbar auf den Reaktionsmechanismus geschlossen werden.^[14] Ein Beispiel ist die Reaktion von Iod ${\ce {I2}}$ und Wasserstoff ${\ce {H2}}$ zu Iodwasserstoff ${\ce {HI}}$ :

${\ce {I2 + H2 -> 2HI}}$

Die beobachtete phänomenologische Reaktionskinetik ergibt anscheinende partielle Reaktionsordnungen von eins in Bezug auf ${\ce {I2}}$ und ${\ce {H2}}$ sowie eine anscheinende Gesamtreaktionsordnung von zwei. Dies ist mit der Vorstellung kompatibel, dass eine einen bimolekularen Stoß von ${\ce {I2}}$ mit ${\ce {H2}}$ umfassende bimolekulare Elementarreaktion stattfindet. Tatsächlich ist dies nicht der Fall; die zu ${\ce {HI}}$ führenden Reaktionspfade beinhalten vielmehr die Reaktion von Iod-Radikalen ${\ce {I.}}$ .^[15]^[16]

Gebrochene Reaktionsordnungen

Zusammengesetzte und gekoppelte Reaktionen weisen häufig gebrochene Reaktionsordnungen wie 1,5 auf, die keine natürlichen Zahlen sind. Ein Beispiel hierfür sind radikalische Polymerisationen, in deren Verlauf ein Initiator ${\ce {I}}$ und ein Monomer ${\ce {M}}$ zu einem Polymer ${\ce {P}}$ reagieren. Zunächst zerfällt ${\ce {I}}$ in Radikale ${\ce {R.}}$ :

${\ce {I -> 2 R.}}$

Hierauf folgt der Kettenstart:

${\ce {{R.}+ M -> R-M.}}$

Auf den Kettenstart folgt das Kettenwachstum:

${\ce {{R-M{_{n}}-M.}+M->R-M{_{n{\text{+}}1}}-M.}}$

Zu berücksichtigen sind außerdem die Kettenabbruchreaktionen. Kettenabbruch kann einerseits durch Rekombination wachsender Kettenenden stattfinden:

${\ce {{R-M{_{n}}.}+R-M{_{m}}.->R-M_{m{+}n}-R}}$

Andererseits kann Kettenabbruch durch Disproportionierung erfolgen:

${\ce {{R-M{_{m}}.}+R-M{_{n}}.->{R-M{_{m}}-H}+R-M_{n}}}$

Betrachtet man die Konzentration der Kettenträger ${\ce {R-M{_{n}}.}}$ unter Anwendung des Bodensteinschen Quasistationaritätsprinzips näherungsweise als konstant, weisen radikalische Polymerisation bei großen Polymerisationsgraden eine Gesamtreaktionsordnung von 1,5 auf. Die partielle Reaktionsordnung in Bezug auf Monomer ${\ce {M}}$ ist 1, die partielle Reaktionsordnung in Bezug auf den Initiator ${\ce {I}}$ 0,5. Mit der Geschwindigkeitskonstanten $k$ erhält man so als Geschwindigkeitsgesetz:^[17]

$r=k\cdot [{\rm {M]\cdot [{\rm {I]^{1/2}}}}}$

Gemischte Reaktionsordnungen

In komplexen Geschwindigkeitsgesetzen kann ein Ausgangsstoff ${\ce {A}}$ mit verschiedenen partiellen Reaktionsordnungen auftreten. Derartige Geschwindigkeitsgesetze enthalten mindestens zwei Potenzfunktionen der Konzentration ${\ce {[A]}}$ von ${\ce {A}}$ , die nicht zu einer Potenzfunktion zusammengefasst werden können. Ein Beispiel hierfür ist:

$r=k_{1}[A]+k_{2}[A]^{2}$

Hierbei tritt ${\ce {[A]}}$ im ersten Summand mit der partiellen Reaktionsordnung (oder der pseudo-Reaktionsodnung) eins, im zweiten Summand mit der partiellen Reaktionsordnung (oder der pseudo-Reaktionsordnung) zwei auf. Man spricht dann von gemischter 1. und 2. Reaktionordnung.^[18] Sofern die Geschwindigkeitskonstanten $k_{1}$ und $k_{2}$ vergleichbare Werte haben, weist die Reaktion bei kleinen Werten von ${\ce {[A]}}$ näherungsweise eine Kinetik 1. Ordnung (oder pseudo-erster Ordnung) auf, bei großen Werten von ${\ce {[A]}}$ eine Kinetik 2. Ordnung (oder pseudo-zweiter Ordnung). Daher kann eine erartige Reaktion zunächst eine phänomenologische Reaktionsordnung von zwei aufweisen, die aufgrund des Verbrauchs des Ausgangsstoffes ${\ce {A}}$ abnimmt, bis die phänomenologische beobachtbare Reaktionsordnung eins wird.

Geschwindigkeitsgesetze können weiterhin Brüche mit zwei oder mehreren Termen enthalten. Ein Grund hierfür ist, dass für Reaktionen mit komplexen Mechanismen für verschiedene Konzentrationen der Ausgangsstoffe verschiedene Elementarreaktionen als langsamster und damit geschwindigkeitsbestimmender Schritt fungieren. Ein Beispiel ist die Oxidation von Alkoholen zu Ketonen durch Hexacyanoferrat(III)-Ionen ${\ce {[Fe(CN)6]^{3-}}}$ unter Katalyse mit Ruthenium(VI)-Ionen ${\ce {RuO4^{2-}}}$ .^[19] Das Geschwindigkeitsgesetz lautet:

$r={\frac {\ce {{\big [}[Fe(CN)6]^{3-}{\big ]}}}{k_{\alpha }+k_{\beta }{\ce {{\big [}[Fe(CN)6]^{3-}{\big ]}}}}}$

Hierbei sind $k_{\alpha }$ und $k_{\beta }$ Geschwindigkeitskonstanten. Wenn ${\ce {{\it {k}}_{\alpha }<<{\it {k}}_{\beta }{\big [}[Fe(CN)6]^{3-}{\big ]}}}$ ist, wäre die partielle Reakionsordnung in Bezug auf ${\ce {[Fe(CN)6]^{3-}}}$ sowie die Gesamtreaktionsordnung null, und die Pseudogeschwindigkeitskonstante der Reaktion wäre $1/k_{\beta }$ . Wird durch den sukzessiven Verbrauch von ${\ce {[Fe(CN)6]^{3-}}}$ hingegen ${\ce {{\it {k}}_{\alpha }>>{\it {k}}_{\beta }{\big [}[Fe(CN)6]^{3-}{\big ]}}}$ , wird die partielle Reaktionsordnung in Bezug auf ${\ce {[Fe(CN)6]^{3-}}}$ sowie die gesamte Reaktionsordnung eins, und die Pseudogeschwindigkeitskonstante der Reaktion wäre $1/k_{\alpha }$ .

Weitere Beispiele für Reaktionsmechanismen, die zu Geschwindigkeitsgesetzen führen, in denen Zähler mit zwei Termen mit verschiedenen Reaktionsordnungen in Bezug auf einen Ausgangsstoff auftreten, sind der Michaelis–Menten-Mechanismus für Enzymkatalyse und der Lindemann-Mechanismus.

Beispiele

Wasserstoffoxidation

Numerische Lösung, mithilfe von

scipy.integrate.odeint. Die Reaktionsraten $k_{1},k_{2}$ und die Anfangskonzentrationen sind in diesem Beispiel beliebig gewählt. $c_{0}$ ist eine Referenzkonzentration.

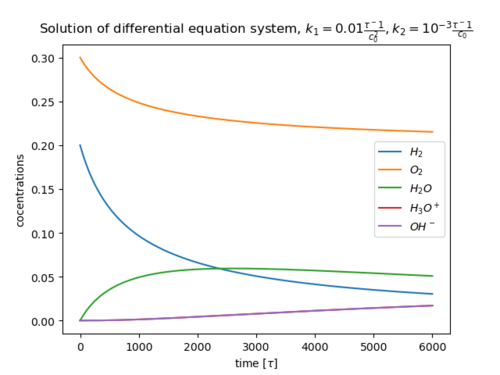
Als Beispiel für ein System aus Differentialgleichungen, die jeweils Geschwindigkeitsgesetze von Elementarreaktionen sind und die für die Kinetik einer Gesamtreaktion relevant sind, wird die Oxidation von Wasserstoff herangezogen:

$\displaystyle \mathrm {2H_{2}+O_{2}\longrightarrow 2H_{2}O}$

(Geschwindigkeitskonstante: $\displaystyle k_{1}$ )

ein Teil dissoziiert

$\displaystyle \mathrm {2H_{2}O\longrightarrow H_{3}O^{+}+OH^{-}}$

(Geschwindigkeitskonstante: $\displaystyle k_{2}$ )

Die Geschwindigkeitsgesetze (Gl.1) für die fünf Spezies lauten:

${\frac {\mathrm {d} }{\mathrm {d} t}}\mathrm {[H_{2}]} =-2k_{1}\mathrm {[H_{2}]^{2}[O_{2}]}$

${\frac {\mathrm {d} }{\mathrm {d} t}}\mathrm {[O_{2}]} =-k_{1}\mathrm {[H_{2}]^{2}[O_{2}]}$

${\frac {\mathrm {d} }{\mathrm {d} t}}\mathrm {[H_{2}O]} =+2k_{1}\mathrm {[H_{2}]^{2}[O_{2}]} -2k_{2}\mathrm {[H_{2}O]^{2}}$

${\frac {\mathrm {d} }{\mathrm {d} t}}\mathrm {[H_{3}O^{+}]} =+k_{2}\mathrm {[H_{2}O]^{2}}$

${\frac {\mathrm {d} }{\mathrm {d} t}}\mathrm {[OH^{-}]} =+k_{2}\mathrm {[H_{2}O]^{2}}$

Einzelnachweise

↑ Eintrag zu rate law (empirical differential rate equation). In: IUPAC (Hrsg.): Compendium of Chemical Terminology. The “Gold Book”. doi: 10.1351/goldbook.R05141 – Version: 5.0.0.
↑ Wladimir Reschetilowski: Kinetik heterogen katalysierter Reaktionen und Reaktionsmechanismen. In: Einführung in die Heterogene Katalyse. Springer Berlin Heidelberg, Berlin, Heidelberg 2015, ISBN 978-3-662-46983-5, "7.1.1 Oberflächenreaktion als geschwindigkeitsbestimmender Schritt" und "7.1.2 Kinetische Ansätze nach Hougen-Watson", S. 100–121, doi: 10.1007/978-3-662-46984-2_7.
↑ ^{Hochspringen nach: a} ^b Carl Heinz Hamann, Dirk Hoogestraat, Rainer Koch: Grundlagen der Kinetik: Von Transportprozessen zur Reaktionskinetik. Springer, Berlin, Heidelberg 2017, ISBN 978-3-662-49392-2, 4.2.3.3 Heterogene Katalyse, S. 152 ff., doi: 10.1007/978-3-662-49393-9.
↑ ^{Hochspringen nach: a} ^b Gerd Wedler, Hans-Joachim Freund: Lehr- und Arbeitsbuch Physikalische Chemie. 7. Auflage. Wiley-VCH, Weinheim 2019, ISBN 978-3-527-82727-5, 1.5.5 Reaktionen nullter Ordnung.
↑ ^{Hochspringen nach: a} ^b Peter W. Atkins, Julio de Paula: Physikalische Chemie. 5. Auflage. Wiley-VCH, Weinheim 2013, ISBN 978-3-527-33247-2, 21.1.2 Die Reaktionsgeschwindigkeit.
↑ Carl Heinz Hamann, Dirk Hoogestraat, Rainer Koch: Grundlagen der Kinetik: Von Transportprozessen zur Reaktionskinetik. Springer, Berlin, Heidelberg 2017, ISBN 978-3-662-49392-2, 4.2.3.4 Enzymatische Katalyse, S. 167 ff., doi: 10.1007/978-3-662-49393-9.
↑ ^{Hochspringen nach: a} ^b M. Dieter Lechner: Einführung in die Kinetik: Chemische Reaktionskinetik und Transporteigenschaften. Springer, Berlin / Heidelberg 2018, ISBN 978-3-662-57454-6, 3.1.5 Reaktionen mit einer Pseudoordnung, S. 13 f., doi: 10.1007/978-3-662-57455-3.
↑ ^{Hochspringen nach: a} ^b Marcus Elstner: Physikalische Chemie I: Thermodynamik und Kinetik. Springer, Berlin / Heidelberg 2017, ISBN 978-3-662-55363-3, 17.3 Methoden zur Bestimmung der Reaktionsordnung, S. 298 f., doi: 10.1007/978-3-662-55364-0.
↑ M. Dieter Lechner: Einführung in die Kinetik: Chemische Reaktionskinetik und Transporteigenschaften. Springer Berlin Heidelberg, Berlin, Heidelberg 2018, ISBN 978-3-662-57454-6, 3.1 Konzentration in Abhängigkeit von der Zeit, S. 9 ff., doi: 10.1007/978-3-662-57455-3.
↑ ^{Hochspringen nach: a} ^b Carl Heinz Hamann, Dirk Hoogestraat, Rainer Koch: Grundlagen der Kinetik: Von Transportprozessen zur Reaktionskinetik. Springer, Berlin, Heidelberg 2017, ISBN 978-3-662-49392-2, 4.2.1.2.3 Die Bestimmung von Reaktionsordnungen, S. 117 ff., doi: 10.1007/978-3-662-49393-9.
↑ M. Dieter Lechner: Einführung in die Kinetik: Chemische Reaktionskinetik und Transporteigenschaften. Springer, Berlin, Heidelberg 2018, ISBN 978-3-662-57454-6, 3.2 Methode der Anfangsgeschwindigkeit, S. 14 f., doi: 10.1007/978-3-662-57455-3.
↑ M. Dieter Lechner: Einführung in die Kinetik: Chemische Reaktionskinetik und Transporteigenschaften. Springer Berlin Heidelberg, Berlin, Heidelberg 2018, ISBN 978-3-662-57454-6, 3.3 Halbwertszeit, S. 16 f., doi: 10.1007/978-3-662-57455-3.
↑ James H. Espenson: Chemical kinetics and reaction mechanisms (= MacGraw-Hill series in advanced chemistry). 2. Auflage. McGraw Hill, New York, NY 1987, ISBN 978-0-07-113949-6, S. 30–31.
↑ Carl Heinz Hamann, Dirk Hoogestraat, Rainer Koch: Grundlagen der Kinetik: Von Transportprozessen zur Reaktionskinetik. Springer, Berlin, Heidelberg 2017, ISBN 978-3-662-49392-2, 4.2.1.2.2 Gebrochene und formale Reaktionsordnungen, S. 116 ff., doi: 10.1007/978-3-662-49393-9 ( springer.com).
↑ John H. Sullivan: Mechanism of the Bimolecular Hydrogen—Iodine Reaction. In: The Journal of Chemical Physics. Band 46, Nr. 1, 1. Januar 1967, ISSN 0021-9606, S. 73–78, doi: 10.1063/1.1840433 ( aip.org [abgerufen am 17. Dezember 2025]).
↑ Keith J. Laidler: Chemical Kinetics. 3. Auflage. HarperCollins, New York 1998, ISBN 978-0-06-043862-3, 8.4.3 Hydrogen—Iodine Reaction, S. 298 f.
↑ M. Dieter Lechner: Einführung in die Kinetik: Chemische Reaktionskinetik und Transporteigenschaften. Springer, Berlin / Heidelberg 2018, ISBN 978-3-662-57454-6, 5.7.3.1 Radikalpolymerisation, S. 67 ff., doi: 10.1007/978-3-662-57455-3 ( springer.com).
↑ James H. Espenson: Chemical kinetics and reaction mechanisms (= MacGraw-Hill series in advanced chemistry). 2. Auflage. McGraw Hill, New York, NY 1987, ISBN 978-0-07-113949-6, S. 34, 60.
↑ Antonio E. Mucientes, María A. de la Peña: Ruthenium(VI)-Catalyzed Oxidation of Alcohols by Hexacyanoferrate(III): An Example of Mixed Order. In: Journal of Chemical Education. Band 83, Nr. 11, November 2006, S. 1643, doi: 10.1021/ed083p1643.

Basierend auf einem Artikel in:

Wikipedia.de