
Steigung

In der Mathematik, insbesondere in der Analysis, ist die Steigung (auch als Anstieg bezeichnet) ein Maß für die Steilheit einer Geraden oder einer Kurve.
Das Problem, die Steigung zu ermitteln, stellt sich dabei nicht nur bei geometrischen Fragestellungen, sondern beispielsweise auch in der Physik oder in der Volkswirtschaftslehre. So entspricht etwa die Steigung in einem Zeit-Weg-Diagramm der Geschwindigkeit oder die Steigung in einem Zeit-Ladungs-Diagramm der Stromstärke.
Steigung einer Geraden
Definition und Berechnung
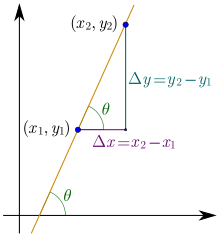
Die Steigung einer Geraden wird häufig durch den Buchstaben
bezeichnet. Verwendet man kartesische
Koordinaten, so hat die Gerade, die durch zwei Punkte
und
festgelegt ist, die Steigung
(sprich: Delta x) bedeutet dabei die Differenz der x-Werte,
entsprechend die Differenz der zugeordneten y-Werte.
Für die durch die Punkte
und
ergibt sich beispielsweise die Steigung:
Es spielt keine Rolle, von welchen Punkten der Geraden man die Koordinaten in
die Formel einsetzt. Nimmt man zum Beispiel
und
,
so erhält man:
Steigt die Gerade an (in positiver x-Richtung, also von links nach rechts betrachtet), so ist ihre Steigung positiv. Für eine fallende Gerade ist die Steigung negativ. Steigung 0 bedeutet, dass die Gerade waagrecht, also parallel zur x-Achse verläuft.
Hat die Gerade die Steigung
und schneidet sie die y-Achse im Punkt
,
so hat sie die Gleichung
Hinweis: Die zur y-Achse parallelen Geraden sind keine Funktionsgraphen und haben deshalb auch keinen Steigungswert. Man kann ihnen die Steigung „unendlich“ (∞) zusprechen.
Straßenverkehr


Die Steigung einer Geraden spielt auch im Straßenverkehr eine Rolle. Das Verkehrszeichen für die Steigung bzw. das Gefälle einer Straße basiert auf dem gleichen Steigungsbegriff, allerdings wird sie meist in Prozent ausgedrückt. Eine Angabe von 12 % Steigung bedeutet zum Beispiel, dass pro 100 m in waagerechter Richtung die Höhe um 12 m zunimmt. Nach der oben gegebenen Definition hat man 12 m durch 100 m zu dividieren, was zum Ergebnis 0,12 führt (in Prozent-Schreibweise 12 %).
Die steilste Straße der Welt ist die Ffordd Pen Llech in Harlech (Wales). Die maximale Steigung beträgt 1:2,67 (19,3° oder ca. 37,45 %).
Eine Verhältnisangabe wie 1:2,67 ist eine weitere Möglichkeit, Neigungen bzw. Steigungen zu definieren. Sie gibt, ebenso wie eine prozentuale Angabe, den Höhenunterschied pro Horizontalstrecke an: 1 m Höhe auf 2,67 m Strecke = 1/2,67 ≈ 0,37453 ≈ 37,45 % (= 37,45 m Höhe auf 100 m Strecke). Auch Böschungen werden so angegeben. Das oft verwendete Verhältnis künstlicher Böschungen von 1:1,5 (abhängig vom Material usw.) ergibt 1 Meter Höhenunterschied auf 1,5 Meter Horizontalstrecke. Das bedeutet eine Steigung von 66,7 % sowie einen Steigungswinkel von arctan(1/1,5) = 33,7°.
Steigungs- oder Neigungswinkel
Aus der Steigung einer Geraden lässt sich mit Hilfe der Tangens- und
Arcustangens-Funktion der zugehörige Steigungs- bzw. Neigungswinkel der
Geraden bezogen auf die positive -Achse
berechnen:
Ein Zusammenhang aus der Trigonometrie
besagt, dass in einem rechtwinkligen
Dreieck der Tangens
von einem der beiden spitzen Winkel
gleich dem Quotienten der jeweiligen
Gegen- und Ankathete ist, womit klar wird, dass die Steigung zugleich der
Tangens des Steigungswinkels (in Grad) gegenüber der positiven -Achse
ist:
Bei der Angabe in Prozent (%) ist zu beachten, dass Steigung und Steigungswinkel nicht proportional zueinander sind, es also auch nicht möglich ist, Steigungen und Steigungswinkel mit einem einfachen Dreisatz ineinander umzurechnen. So entspricht beispielsweise der Steigung 1 (= 100 %) ein Steigungswinkel von 45°, der Steigung 2 (= 200 %) dagegen nur noch ein Winkel von rund 63,4°, und für einen Steigungswinkel von 90° schließlich müsste die Steigung ins Unendliche wachsen.
Annähernde Proportionalität von Steigung und Steigungswinkel dagegen ist nur
für kleine Steigungswinkel bis etwa 5° gegeben – so entspricht einer
Steigung von ±0,01 bzw. ±1 % ein Steigungswinkel von annähernd ±0,57°, und
umgekehrt ein Steigungswinkel von ±1° einer Steigung von annähernd ±0,0175 bzw.
1,75 %. Mathematisch lässt sich das dadurch erklären, dass die Ableitung des
Tangens in 0 gerade gleich 1 ist, d.h. für Werte von
in der Nähe von 0 gilt
.
Für größere Steigungswinkel dagegen, oder wenn ihre Größe exakt bestimmt werden soll, benötigt man die Umkehrfunktion des Tangens, das heißt die Arcustangens-Funktion:
Im obigen Beispiel errechnet man:
Bei negativen Steigungen ist hier zu beachten, dass – aufgrund der Punktsymmetrie der
Arcustangens-Funktion – dann auch die Steigungswinkel
negativ werden.
Schnittwinkel
Der Steigungsbegriff liefert auch eine bequeme Methode, den Schnittwinkel
zweier Geraden mit gegebenen Steigungen
und
zu bestimmen:
Zwei Geraden sind genau dann parallel (
= 0°), wenn ihre Steigungen übereinstimmen. Sie sind genau dann senkrecht
zueinander (
= 90°), wenn ihre Steigungen die Orthogonalitäts-Bedingung
·
= −1 erfüllen.
Steigung von Gewinden
Bei metrischen Gewinden kennzeichnet die Steigung die Ganghöhe, das heißt den Abstand zwischen zwei Gewindestufen entlang der Gewindeachse, anders gesagt den axialen Weg, der durch eine Umdrehung des Gewindes zurückgelegt wird.
Bei zölligen Gewinden dagegen wird als Wert die Anzahl der Gewindegänge auf der Strecke von einem Zoll angegeben. Als Pseudoeinheit wird oft die Abkürzung TPI ("threads per inch") verwendet.
Gefälle an Gewässern, in potentialgetriebenen Prozessen und Strömungen
Insbesondere an Wasserkraftwerken wird der lokale Wasserspiegelunterschied zwischen Oberwasser und Unterwasser als Gefälle (oder auch Arbeitshöhe) bezeichnet. Das gilt für Mühlen, Laufkraftwerke aber auch für Konstruktionen mit Stollen, Wasserschlössern und Druckrohren. Auch die Abnahme der Wasserspiegelhöhe zwischen 2 längs eines Fließgewässers bestimmten entfernten Punkten wird als Gefälle bezeichnen.
In Wärmekraftprozessen, etwa an Wärmekraftmaschinen oder Kälteaggregaten, wird von Druck- und Temperaturgefällen gesprochen, wenn diskrete Unterschiede entsprechenden Messgrößen zwischen 2 Bereichen bestehen, die zu von selbst ablaufenden Strömen von Fluiden (Gas, Flüssigkeit) bzw. Wärmeenergie führen.
Statische Druckgefälle können auch zwischen verschiedenen Punkten von Versorgungssystemen für Druckluft oder Leitungswasser, sowie in Lüftungsanlagen (bedeutsam für Hygiene, Reinraum, Geruchsbelästigung) bestehen. (Dynamisch tritt Druckabfall längs einer Strömungsstrecke auf.)
Chemisch-physikalische Prozesse werden mitunter durch ein räumlich bestehendes stoffliches Konzentrationsgefälle angetrieben. Osmose, Diffusion, Chromatografie, Kristallisation aus Lösung, Verdunstung seien hier genannt.
Im übertragenen Sinn werden analog in Ökonomie und Soziologie Unterschiede von Lohnniveau, Preisniveau oder Bildung, etwa regional zwischen Stadt und Land, sozial zwischen Mann und Frau als Lohngefälle, Preisgefälle, Bildungsgefälle bezeichnet.
In all diesen Fällen ist abweichend vom sonst üblichen Begriffsinhalt von Gefälle (als negativer Steigung) nicht eine Neigung im Sinn von Höhenunterschied pro Entfernung (Länge) und damit der Maßeinheit 1, sondern eine Höhendifferenz (gemessen in der Maßeinheit Meter) gemeint. Allen dadurch getriebenen Strömungsprozessen ist gemein (von selbst) nur in eine Richtung - gefälleabwärts - abzulaufen. (Vgl. Potentialunterschied.)
Verallgemeinerung: Steigung einer Kurve
Eines der grundlegenden Probleme der Analysis besteht darin, die Steigung einer Kurve in einem gegebenen Kurvenpunkt herauszufinden. Die oben besprochene Formel ist jetzt nicht mehr verwendbar, da nur ein Punkt gegeben ist. Wählt man den zweiten Punkt willkürlich, erhält man kein eindeutiges Ergebnis oder, falls beide Punkte identisch gewählt werden, ist das Ergebnis nicht definiert, da durch 0 geteilt wird.
Man definiert die Steigung des Graphen einer Funktion in einem Punkt des Graphen daher als Steigung der Kurventangente in diesem Punkt. Die Differenzialrechnung liefert den Begriff der Ableitung als Hilfsmittel, um solche Steigungswerte ausrechnen zu können.
Beispiel: Für den Graphen der Funktion
sollen die Steigung im Kurvenpunkt
und der zugehörige Neigungswinkel berechnet werden.
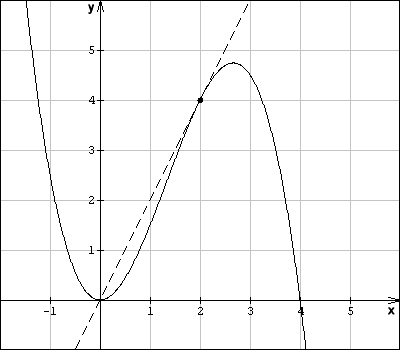
Zunächst ermittelt man die Gleichung der Ableitungsfunktion :
Nun wird die x-Koordinate des gegebenen Punktes eingesetzt:
Aus dem Wert der Steigung ergibt sich der Neigungswinkel:
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 21.01. 2023