
Schergeschwindigkeit
Die Schergeschwindigkeit (ältere, nicht DIN-konforme Bezeichnungen:
Schergefälle, Scherrate, Geschwindigkeitsgefälle, Symbol
(Gamma punkt); früher: D, Dimension
T−1 ) ist ein Begriff aus der Kinematik,
der bei Flüssigkeiten
die räumliche Veränderung der Flussgeschwindigkeit
bezeichnet. Da in realen Flüssigkeiten Reibungskräfte vorhanden sind, bedeutet
eine Scherung
eines Fluids
genauso wie bei einem Festkörper
eine Übertragung von Kraft. In der Rheologie
dient die Schergeschwindigkeit als Maß für die mechanische Belastung, der eine
Probe bei einer rheologischen Messung unterworfen wird.
Messung der Viskosität
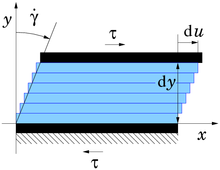
Die Schergeschwindigkeit wird in der Rheologie zur Definition der Viskosität η verwendet,
die der Proportionalitätsfaktor zwischen Schubspannung
und Schergeschwindigkeit ist:
.
Betrachtet wird eine Schichtenströmung zwischen zwei Platten wie im Bild. Die
Schergeschwindigkeit berechnet sich dann aus dem Verhältnis zwischen dem
Geschwindigkeitsunterschied
zweier benachbarter Flüssigkeitsschichten und deren Abstand
:
Bei kleinem Abstand der Platten kann eine über die Höhe lineare
Geschwindigkeitsverteilung wie im Bild angenommen werden und die
Schergeschwindigkeit ist die Geschwindigkeit der oberen Platte dividiert durch
den Abstand der Platten. Im Grenzübergang
entsteht die Ableitung der Geschwindigkeit u nach der Koordinate y.
In komplizierteren Strömungen kann eine Scherung auch durch eine Änderung der vertikalen Geschwindigkeitskomponente v in horizontaler x-Richtung erfolgen. Weil beide Richtungen gleichberechtigt sind, bietet sich die Verallgemeinerung
an. Bei der Schichtströmung hier kann freilich der zweite Term mit der Geschwindigkeit v senkrecht zu den Platten vernachlässigt werden. In axialsymmetrischen Strömungen wird vorteilhaft ein Zylinder- oder Kugelkoordinatensystem zugrunde gelegt, in dem dann die Radialgeschwindigkeit an den Wänden verschwindet.
Allgemeine Definition
Mathematisch ausgedrückt bestimmt sich die Schergeschwindigkeit aus den Komponenten des Geschwindigkeitsgradienten, der ein Tensor zweiter Ordnung ist:
Die Geschwindigkeitsanteile
beziehen sich auf ein kartesisches
Koordinatensystem mit den Koordinaten x, y und z. Die Schergeschwindigkeit
berechnet sich mit dem symmetrischen
Anteil des Gradienten, dem Verzerrungsgeschwindigkeitstensor
Das Superskript
steht für die transponierte
Matrix. In der Kontinuumsmechanik
wird auch das kleine d als Bezeichnung benutzt, weil dieser Tensor in Euler'scher
Betrachtungsweise formuliert ist. Die Schergeschwindigkeit in einer Ebene,
die von zwei zueinander senkrechten Vektoren
der Länge eins aufgespannten wird, ergibt sich dann aus dem Produkt
Bei der Schichtströmung oben sind die Vektoren
parallel zur x- bzw. y-Richtung und es ergibt sich, wenn die Strömung wie im
Bild in x-Richtung und in der x-y-Ebene stattfindet
denn der Term mit der Geschwindigkeit
senkrecht zu den Platten kann wie gesagt vernachlässigt werden.
Literatur
- H. Altenbach: Kontinuumsmechanik. Springer, 2012, ISBN 978-3-642-24118-5.
- DIN 1342-1
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 09.06. 2023