Viskosität

Name

dynamische Viskosität

$\eta$ , $\mu$

Größen- und Einheitensystem	Einheit	Dimension
SI	Pa·s = N·s·m⁻² = kg·m⁻¹·s⁻¹	M·L⁻¹·T⁻¹
cgs	P	M·L⁻¹·T⁻¹

Die Viskosität bezeichnet die Zähflüssigkeit oder Zähigkeit von Flüssigkeiten und Gasen (Fluiden). Je höher die Viskosität ist, desto dickflüssiger (weniger fließfähig) ist das Fluid; je niedriger die Viskosität, desto dünnflüssiger (fließfähiger) ist es.

Ohne weitere Angaben ist der Widerstand des Fluids gegenüber Scherung gemeint. Sie wird daher als Scherviskosität bezeichnet, zur Abgrenzung gegenüber der Dehnviskosität bei Dehnung sowie der Volumenviskosität bei gleichmäßigem Druck. Des Weiteren wird zwischen der dynamischen Viskosität und der kinematischen Viskosität unterschieden. Die dynamische Viskosität ist das Verhältnis von Schubspannung und Geschwindigkeitsgradient. Der Kehrwert der dynamischen Viskosität ist die Fluidität. Die dynamische Viskosität $\eta$ und die kinematische Viskosität $\nu$ stehen über die Dichte $\rho$ in direktem Zusammenhang, $\eta =\nu \cdot \rho$ .

Physikalische Größe

Name

kinematische Viskosität

Formelzeichen

$\nu$

Größen- und Einheitensystem	Einheit	Dimension
SI	m²·s⁻¹	L²·T⁻¹
cgs	St	L²·T⁻¹

Teilchen zäher Flüssigkeiten sind stärker aneinander gebunden und somit weniger beweglich; man spricht von der inneren Reibung. Sie resultiert nicht nur aus den Anziehungskräften zwischen den Teilchen des Fluids (Kohäsion). Bei dünnflüssigeren Fluiden resultiert die Viskosität aus einem Impulsfluss im Fluid. Die Viskosität von Feststoffen ist vergleichsweise hoch und damit schwer bestimmbar. Statt Viskosität werden Begriffe wie Verlustfaktor, Speicher- und Verlustmodul verwendet.

Das Wort Viskosität geht auf den typisch zähflüssigen Saft der Beeren in der Pflanzengattung Misteln (Viscum) zurück. Aus solchen Misteln wurde Vogelleim gewonnen. „Viskos“ bedeutet „zäh wie Vogelleim“.

Die blaugrüne Flüssigkeit links ist niederviskos wie Wasser, die orange rechts hochviskos wie Honig.

Die Viskosität taucht in der Berechnung des viskosen Spannungstensors auf.

Definition

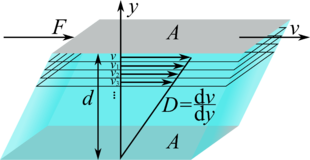
Abbildung 2: Definition der Viskosität: Das Fluid (blau) wird zwischen ruhender Platte (unten) und bewegter Platte (oben) geschert.

Man stelle sich zwei im Abstand parallel angeordnete Platten der Fläche vor. Zwischen diesen Platten befindet sich eine Flüssigkeit, die an beiden Platten haftet. In unserer Vorstellung soll der Raum mit der Flüssigkeit in Schichten unterteilt sein. Wird nun die obere Platte mit der Geschwindigkeit bewegt, so bewegt sich die Schicht in unmittelbarer Nachbarschaft auf Grund der Haftung ebenfalls mit der Geschwindigkeit . Da die untere Platte ruht, ruht auch ihre Nachbarschicht. Die innenliegenden Flüssigkeitsschichten gleiten mit unterschiedlichen Geschwindigkeiten aneinander vorbei. Die Geschwindigkeit nimmt von der ruhenden Platte zur bewegten zu.

Von der obersten, an der Platte haftenden Schicht geht eine Tangentialkraft auf die darunterliegende Schicht aus. Diese bewegt sich folglich mit der Geschwindigkeit $v_{1}.$ Diese Schicht wirkt wiederum auf die darunterliegende Schicht und bewegt sie mit der Geschwindigkeit $v_{2}.$

Im Experiment lässt sich zeigen, dass im Idealfall die Kraft , die nötig ist, um die obere Platte zu bewegen, proportional zur Fläche , dem Geschwindigkeitsunterschied $\Delta v$ und antiproportional zum Abstand der Platten $\Delta y$ ist:

$F \sim A$ und $F \sim \Delta v$ und $F \sim \frac{1}{\Delta y}$

Hieraus ergibt sich die Gleichung

$F=\eta A{\frac {\Delta v}{\Delta y}}$

Die Proportionalitätskonstante $\eta$ ist die dynamische Viskosität. Die Änderung der Geschwindigkeit senkrecht zur Bewegungsrichtung, also der Geschwindigkeitsgradient

${\dot {\gamma }}={\frac {\Delta v}{\Delta y}}={\frac {\mathrm {d} v}{\mathrm {d} y}}$

auch mit oder bezeichnet, wird Verformungsgeschwindigkeit, Schergeschwindigkeit oder Scherrate genannt. Mit der Schubspannung

$\tau=\frac{F}{A}$

ergibt sich der Zusammenhang

$\tau =\eta \cdot {\dot {\gamma }}$

Einheiten

Im SI-Einheitensystem gilt: Ein Stoff, der sich zwischen zwei Platten befindet, hat die dynamische Viskosität 1 N s/m², wenn bei einer Größe der Platten von 1 m² und einem Plattenabstand von 1 m eine Kraft von 1 N benötigt wird, um die Platten mit einer Geschwindigkeit von 1 m/s gegeneinander zu verschieben. Für die physikalische Einheit der dynamischen Viskosität gilt also:

$1\,{\rm {N}}=[\eta ]\cdot \left({\frac {{\rm {m}}^{2}\,{\rm {m}}}{{\rm {m}}\,{\rm {s}}}}\right)\Rightarrow [\eta ]={\frac {{\rm {N}}\cdot {\rm {s}}}{{\rm {m}}^{2}}}=\mathrm {\frac {kg}{m\cdot s}} ={\rm {1\,Pa\cdot s}}$

Für die SI-Einheit der kinematischen Viskosität gilt:

$[\nu ]={\frac {\rm {m^{2}}}{\rm {s}}}$

In der Praxis wird für die dynamische Viskosität neben der Pa·s (Pascalsekunde) außerdem der tausendste Teil der SI-Einheit mPa·s (Millipascalsekunde) für Medien niedriger Viskosität verwendet.

Im CGS-System wird die dynamische Viskosität in Poise (P) gemessen, wobei 1 Ns/m² = 1 Pa·s = 10 Poise = 1000 Centipoise = 1000 cP = 1 kg/ms, und die kinematische Viskosität in Stokes (St), 1 St = 10⁻⁴ m²/s.

Das Engler-Grad ist eine veraltete Einheit für die Viskosität. Diese Einheit gibt die Viskosität im Vergleich zu Wasser an.

Viskosität von Flüssigkeiten

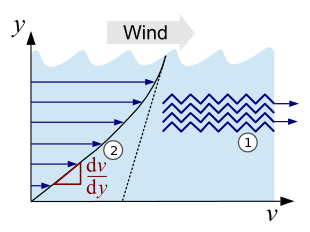
Abbildung 1: Modellvorstellung zur Viskosität: Links eine Veranschaulichung zum Geschwindigkeitsgradient (2), sowie die Form des Gradienten für den Betrag der Geschwindigkeit (gestrichelt). Rechts eine Veranschaulichung für die verzahnten Molekülschichten (1).

Den Effekt innerer Reibung kann man sich vereinfacht durch die Bewegung zweier übereinander liegender, verzahnter Molekülschichten vorstellen (siehe Abb. 1, Punkt 1). Beim Fließen gleiten die Moleküle aneinander vorbei, und um die Verzahnung zu überwinden, benötigt man eine gewisse Kraft. Den Zusammenhang zwischen dieser Kraft und den Eigenschaften des vorliegenden Fluids definiert die Viskosität. Erkennbar wird dieser Zusammenhang besonders gut an der homologen Reihe der Alkane (kettenförmige Kohlenwasserstoffe), hier steigt die Viskosität mit der Kettenlänge und damit den zunehmenden intermolekular wirkenden Van-der-Waals-Kräften kontinuierlich an. Bei den mittleren Alkanen (ab Nonan, neun C-Atome) hat sie bereits einen Wert ähnlich dem von Wasser.

Sehr gut veranschaulichen kann man sich die Viskosität auch an folgendem Beispiel: gleitet Wind über das Wasser eines Ozeans, erzeugt dies eine Bewegung der Wasserschicht an der Oberfläche. Je tiefer man nun taucht, desto ruhiger wird das Wasser, bis man einen Punkt erreicht, wo keine Strömung herrscht. Die einzelnen Flüssigkeitsschichten bewegen sich mit unterschiedlicher Geschwindigkeit , es entsteht ein Geschwindigkeitsgradient (siehe Abb. 1, Punkt 2).

Newtonsche Fluide

Handelt es sich um sehr dünne Fluidschichten, so ist der Geschwindigkeitsverlauf linear, wie in obiger Herleitung. Dieser Zusammenhang wurde bereits 1687 von Isaac Newton unterstellt:

“The resistance which arises from the lack of slipperiness originating in a fluid – other things being equal – is proportional to the velocity by which the parts of the fluid are being separated from each other.”

„Der Widerstand, der durch den Mangel an Gleitfähigkeit innerhalb einer Flüssigkeit entsteht, ist – vorausgesetzt, dass alle anderen Bedingungen gleich bleiben – proportional zu der Geschwindigkeit, mit der die Flüssigkeitsteilchen voneinander getrennt werden.“

– Isaac Newton: Philosophiae Naturalis Principia Mathematica

Abbildung 3: Schubspannungs-Schergeschwindigkeits-Diagramm:
1: Scherverzähendes (dilatantes) Fluid
2: Newtonsches Fluid
3: Scherverdünnendes (pseudoplastisches) Fluid
4: Bingham-plastisches Fluid
5: Casson-plastisches Fluid
Nach rechts ist die Schergeschwindigkeit und nach oben die daraus resultierende Schubspannung angetragen.

Flüssigkeiten, die diesem linearen Zusammenhang folgen, werden deswegen als newtonsche Fluide bezeichnet. Ist $\eta$ von abhängig, so bezeichnet man die Flüssigkeit als nicht-newtonsch. Beim newtonschen Viskositätsgesetz wird stets laminare Strömung sowie Temperatur- und Druckunabhängigkeit der Flüssigkeitseigenschaften angenommen. Für diese Stoffe stellt sich das im Schubspannungs-Schergeschwindigkeits-Diagramm gezeigte, lineare Geschwindigkeitsprofil ein (Abb. 3, Kurve 2: Newtonsches Fluid).

In den rheologischen Modellen wird das newtonsche Verhalten durch das Newton-Element, einem Dämpfungszylinder ähnlich einem Stoßdämpfer, dargestellt.

Nicht-newtonsche Fluide

Viele Substanzen folgen diesem Gesetz jedoch nicht, sondern zeigen ein zeit- oder chergeschwindigkeitsabhängiges Verhalten. Dabei unterscheidet man verschiedene Arten der Abweichung:

Fließgrenze, es muss erst eine gewisse Mindestschubspannung vorhanden sein, um ein Fließen zu erreichen (plastisches Fließen). Diese Art Fluid wird auch als Bingham-Fluid bezeichnet
Strukturviskosität / Dilatanz, dabei ist die Viskosität $\eta$ keine Konstante, sondern ändert sich mit dem Schergefälle ${\dot {\gamma }}$
Thixotropie / Rheopexie, hierbei zeigen sich zeitabhängige Strukturveränderungen, so dass je nach Zeitdauer seit der letzten Fließbewegung andere Viskositätswerte zu finden sind.

Im allgemeinen Fall muss das Schergefälle ${\dot {\gamma }}$ aus dem Scherwinkel in der Flüssigkeit berechnet werden und nicht über den Geschwindigkeitsgradienten. Das Verhältnis $\frac{\tau}{\dot\gamma}$ wird in diesem Fall auch scheinbare Viskosität genannt.

Viskoelastische Materialien können mit der komplexen Viskosität, bei der von einer sinusförmigen Scherung ausgegangen wird, beschrieben werden.

Typische nicht-newtonsche Fluide sind zusammengesetzte Substanzen wie Blut und Ketchup. Da Blut sowohl aus den festen Substanzen des Hämatokrits als auch des Blutplasmas besteht, das Mischungsverhältnis jedoch stark variiert, verändert sich auch die Viskosität. Bei hohem Anteil der festen Substanzen ist z.B. die Leistungsfähigkeit in Ausdauer-Sportarten deutlich erhöht, bei zu hohen durch Doping kann dies zum Tod führen.

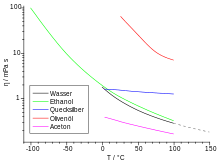
Temperaturabhängigkeit

Die dynamische Viskosität der meisten Flüssigkeiten nimmt mit steigender Temperatur ab und kann oft mit der Arrhenius-Andrade-Beziehung beschrieben werden:

$\eta =\eta _{0}\cdot \exp \left({\frac {E_{\mathrm {A} }}{R\cdot T}}\right)$

mit

$\eta_0$ eine Materialkonstante
$E_\mathrm A$ die Aktivierungsenergie (auch Platzwechselenergie)
die allgemeine Gaskonstante
die absolute Temperatur.

Bei Flüssigkeiten in der Nähe (d.h. bis ca. 100 K über) der Glasübergangstemperatur gilt meist die WLF-Beziehung. Hier dominiert nämlich das sehr geringe freie Volumen, das in der Nähe der Glasübergangstemperatur viel stärker von der Temperatur abhängt als die Kettenbeweglichkeit, die hinter der Arrhenius-Andrade-Beziehung steht.

Die Abhängigkeit der kinematischen Viskosität von der Temperatur wird bei Ölen durch den Viskositätsindex beschrieben.

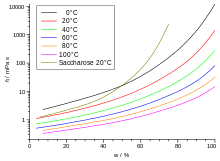
Speziell für Wasser lässt sich die Viskosität im Temperaturbereich zwischen 0 °C und 100 °C mit nachfolgend angegebener Gebrauchsformel ermitteln. Dabei ist die Temperatur in der Einheit Kelvin einzusetzen. Der damit berechnete Wert entspricht der dynamischen Viskosität in der Einheit Pa·s.

$\eta _{\text{Wasser}}={\frac {1}{0,1\cdot T^{2}-34,335\cdot T+2472}}$

Messung

Messanordnungen von links nach rechts: koaxiale Zylinder, Platte-Platte, Kegel-Platte; bewegter Teil in Orange, unbewegter Teil in blassem Violett, Fluid in Hellblau

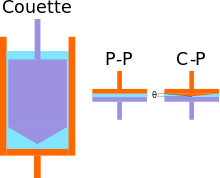
Die Viskosität von Flüssigkeiten kann mit einem Viskosimeter z.B. gemäß EN ISO 3219 gemessen werden. Ein Rheometer ermöglicht es, darüber hinaus noch weitere rheologische Eigenschaften, auch von Festkörpern, zu bestimmen. Bei beiden Gerätetypen wird entsprechend der Viskositätsdefinition die zu messende Probe im Spalt zwischen zwei Körpern (z.B. zwei koaxialen Zylindern oder zwei parallelen Platten) eingebracht. Ein Teil der Anordnung rotiert oder oszilliert mit definierter Geschwindigkeit, während der andere ruht. Aus der Geometrie der Messanordnung und der Geschwindigkeit des bewegten Teiles ergibt sich die Schergeschwindigkeit. Das zur Aufrechterhaltung der Bewegung notwendige Drehmoment wird gemessen, woraus sich dann die Schubspannung und damit die Viskosität ermitteln lässt.

Eine schnelle und einfache, aber auch sehr ungenaue Methode der Viskositätsbestimmung ist der Auslaufbecher.

Typische Werte

Viskosität verschiedener Flüssigkeiten in Abhängigkeit von der Temperatur

Viskosität der Lösungen von Glycerin oder Saccharose (Rohrzucker) in Wasser, in Abhängigkeit vom Massenanteil, für die Glycerinlösungen auch bei unterschiedlichen Temperaturen

Das Pechtropfenexperiment – ein seit 1927 laufendes Langzeitexperiment zur Viskosität von Pech; einem superzähen Material.

Substanz	η in mPa·s (cP)^{[Anm. 1]}
Wasser (5 °C)	1,52
Wasser (10 °C)	1,297
Wasser (20 °C)	1,00
Wasser (25 °C)	0,891
Blut (37 °C)	3 bis 25^{[Anm. 2]}^[8]
Traubensaft	2 bis 5
Olivenöl	≈ 10²
Honig	≈ 10⁴
Sirup	≈ 10⁴ bis 10⁵
Kaffeesahne	≈ 10
Ethylenglycol (20 °C)	20,81
n-Pentan (25 °C)	0,224
n-Hexan	0,320
n-Heptan	0,410
Octan	0,538
Nonan	0,711
Decan	0,920
Dodecan	1,52
Paraffinöl	≈ 10² bis 10⁶
Benzol (25 °C)	0,601
Diethylether	0,240
Diisopropylether	0,33
Ethanol	1,19
Essigsäure (80%ige bei 25 °C)	2,31
Glycerin (rein)	1480
Chloroform	0,56
Lack	≈ 10²
Polymerschmelzen	≈ 10³ bis 10¹³^{[Anm. 3]}^{[Anm. 4]}
Petroleum	0,65
Motoröl (150 °C)	≈ 3
Motoröl (25 °C)	≈ 100
Schweröl RMA 30 (50 °C)	30
Schweröl RMK 700 (50 °C)	700
Bitumen (je nach Sorte)	≈ 10⁷ bis 10¹⁴^{[Anm. 4]}
Asphalt (je nach Rezeptur)	≈ 10¹¹ bis 10¹⁶^{[Anm. 4]}
Quecksilber	1,55
Aluminiumschmelze (700 °C)	≈ 2
Glas (Verarbeitungstemperatur)	≈ 10⁶ bis 10¹²^{[Anm. 4]}
Glas (Raumtemperatur)	≈ 10²² bis 10²⁴^{[Anm. 4]}
Silikatarme Schmelze (Basaltlava) bei 1400 °C	≈ 10⁰ bis 10¹
Silikatreiche Schmelze (Rhyolithlava) bei 1400 °C	≈ 10⁵ bis 10⁷^{[Anm. 4]}
Steinsalz	≈ 10¹⁸ bis 10²¹^{[Anm. 4]}^{[Anm. 5]}

Farblegende: Wasser; Lebensmittel; Kohlenwasserstoffe; Sauerstoff- und Chlorkohlenwasserstoffe; Erdöl-„Produkte“; Metalle; Mineralisches; Sonstiges

Anmerkungen

↑ Sofern nicht anders vermerkt, beziehen sich die Werte auf die Viskosität bei 20 °C. Millipascalsekunden mPa·s sind identisch mit der früher gebräuchlichen Einheit Centipoise cP.
↑ Die Werte für Blut gelten wohl für Vollblut und schwanken stark mit dem Aufenthaltsort in den jeweiligen Blutgefäßen. In Kapillaren sind die sonst oblaten (scheibchenförmigen) roten Blutkörperchen prolat (länglich) verformt, wodurch die Viskosität wesentlich sinkt. Feinste Kapillaren sind überhaupt nur so dick wie einzelne Blutkörperchen, sodass dort sog. Pfropfströmung auftritt, eine Viskosität kann dann nicht mehr sinnvoll definiert werden. In großen Gefäßen stapeln sich rote Blutkörperchen zu langen Aggregaten, wodurch die Viskosität ebenfalls erheblich verringert wird. Weniger viskos ist (gelbliches) Blutplasma und noch geringer aus abgeschürfter Haut dringendes farbloses Wundsekret oder Lymphe. In der Literatur wird die Viskosität von Blut in großen Gefäßen, bei schneller Strömung und bei normalem Hämatokrit mit 3–4 mPa·s angegeben.
↑ Bei Polymeren gibt es einen sehr breiten Bereich an Viskositäten, der im Wesentlichen von der Kettenlänge und deren Verzweigungsstruktur, aber auch von der Schergeschwindigkeit abhängt, da sie Strukturviskosität aufweisen. Es ist deshalb nicht sinnvoll, für Polymere einen einzigen Viskositätswert anzugeben. Die genannten Werte dienen nur als Größenordnung. Hergestellt werden z.B. Silikonöle (PDMS) mit definierten Viskositäten zwischen 0,6 mPa·s bei 25 °C und 1000 Pa·s bei 27 °C. Polymerschmelzen können aber auch noch sehr viel höhere Viskositäten aufweisen. Bei einem UHMW-HDPE (für Hüftgelenksimplantate) wurden bei 150 °C Viskositäten jenseits der 10¹⁰ Pa·s gemessen.
↑ ^a ^b ^c ^d ^e ^f ^g Es muss betont werden, dass die Angabe eines Viskositätswertes allein bei Substanzen mit Viskositäten über 10000 Pa·s nicht mehr sinnvoll ist. Für solche Substanzen sollte stattdessen der komplexe Schubmodul angegeben werden (Thomas Mezger: Das Rheologie Handbuch. Vincentz Network GmbH, 2007). Die hier angegebenen Werte dienen nur der groben Veranschaulichung der Größenordnung.
↑ Die Viskosität eines kristallinen Festkörpers ist prinzipiell unendlich groß. Da auf lange Sicht durch die unvermeidlichen Fehlstellen im Kristallit dennoch eine irreversible Deformation auftreten kann, erhält man bei realen kristallinen Stoffen dennoch zwar sehr große, aber endliche Werte.

Viskosität von Gasen

Bei Fluiden mit niedriger Viskosität entspricht das Bild der inneren Reibung „nicht den physikalisch korrekten Vorstellungen über molekülbedingte Transportvorgänge in Fluiden“. Stattdessen resultiert hier die Viskosität im Fluid aus einem Impulsfluss, der mit dem folgenden Bild veranschaulicht werden kann: Die Stromfäden in der Strömung werden durch Züge versinnbildlicht, die mit unterschiedlicher Geschwindigkeit parallel nebeneinanderher fahren und mit Sandsäcken beladen sind. Die Sandsäcke entsprechen den Fluidelementen im Stromfaden. Personen auf den Zügen werfen die Sandsäcke auf den jeweils anderen Zug, was der zufälligen thermischen Bewegung der Fluidelemente zwischen den Stromfäden gleichkommt. Landet ein Sack des langsameren Zuges auf dem schnelleren, dann nimmt der Sandsack Impuls auf, den der schnellere Zug an ihn abgibt und so selbst langsamer wird. Wenn umgekehrt ein Sack des schnelleren Zuges auf dem langsameren landet, nimmt der Zug den Impuls des Sandsacks auf und wird so selbst schneller. Durch diesen Impulsaustausch wird der schnellere Zug abgebremst und der langsamere beschleunigt.

Viskosität stellt demnach einen Impulsfluss von einem schneller fließenden Stromfaden auf einen langsamer fließenden dar. In einer Kontinuumsströmung tauschen die Fluidelemente Impulse über die zwischen ihnen wirkenden Spannungen aus. Zwischen den unterschiedlich schnell nebeneinanderher fließenden Stromfäden kommt es zu Schubspannungen, die sich makroskopisch als Viskosität bemerkbar machen.

Abschätzung

Viskosität verschiedener Gase bei Normaldruck

Viskosität von Stickstoff in Abhängigkeit vom Druck für verschiedene Temperaturen

Viskosität von Stickstoff in Abhängigkeit von der Temperatur für verschiedene Drücke

Für Gase lässt sich die Viskosität anhand einer mikroskopischen Betrachtung des Impulsflusses abschätzen:

$\eta ={\frac {1}{3}}\,n\,m\,v\,\lambda$

mit der freien Weglänge $\lambda$ für die Gasteilchen, der Masse der Gasteilchen , der mittleren Teilchengeschwindigkeit und der Teilchenzahldichte .

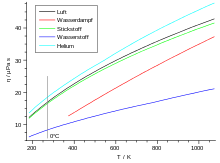
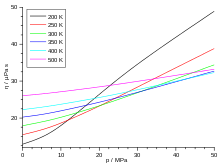
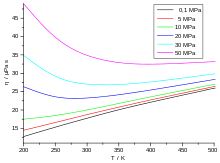
Die Viskosität von Gasen ist bei niedrigen Drücken (≈ 0,1 bis 10 bar) unabhängig vom Druck. Dies gilt solange, wie die freie Weglänge klein gegenüber den Gefäßabmessungen und groß gegenüber den Molekülabmessungen ist. Mit anderen Worten: Für ein sehr dünnes oder ein sehr dichtes Gas wird die Viskosität doch wieder vom Druck beziehungsweise der Dichte des Gases abhängig.

Grundsätzlich abhängig ist die Viskosität aber von der Temperatur. Mit zunehmender Temperatur steigt die Viskosität, da die mittlere Teilchengeschwindigkeit proportional zu $T^{0{,}5}$ wächst (siehe unten). Dieses Verhalten ist bei den meisten Flüssigkeiten genau entgegengesetzt. Die folgende Tabelle listet zu einigen Gasen die Viskositäten und freien Weglängen auf.

Gas unter Normalbedingungen	η in µPa·s	λ in nm
Luft	18,2	059,8
Sauerstoff (O₂)	19,2	063,3
Kohlendioxid (CO₂)	13,8	039,0
Stickstoff (N₂)	16,6	058,8
Argon	21,0	062,6
Neon	29,7	124,0
Helium	18,6	174,0
Wasserstoff (H₂)	08,4	111,0

Kinetische Gastheorie

Nach Hirschfelder kann die Viskosität reiner Gase mit Hilfe der kinetischen Gastheorie in einem großen Temperaturbereich (etwa von 200 bis 3000 Kelvin) berechnet werden.

$\eta ={\frac {5\cdot {\sqrt {\pi \cdot m\cdot k_{\mathrm {B} }\cdot T}}}{16\cdot \pi \cdot \sigma ^{2}\cdot \Omega ^{(2,2)^{\star }}}}$

Hierbei ist die Molekülmasse, $k_{\mathrm {B} }$ die Boltzmann-Konstante, die Temperatur, $\sigma$ der Lennard-Jones-Stoßdurchmesser und $\Omega^{(2,2)^{\star}}$ das reduzierte Stoßintegral, das von der reduzierten Temperatur $T^{\star }=k_{\mathrm {B} }T/\epsilon$ abhängt. $\epsilon$ ist die Energie des Lennard-Jones-Potentials. Werte für die Lennard-Jones-Parameter und das reduzierte Stoßintegral sind in Lienhards Lehrbuch zur Wärmeübertragung in Kapitel 11 aufgeführt. Das reduzierte Stoßintegral $\Omega^{(2,2)^{\star}}$ ist so definiert, dass für ein ideales Gas, bei dem Teilchenwechselwirkungen wie Stöße harter Kugeln betrachtet werden, $\Omega ^{(2,2)^{\star }}=1$ gilt.

Physik des Reibungstensors

Die Viskosität begründet sich aus dem Experiment, nach dem zur Aufrechterhaltung einer Scherströmung eine Kraft erforderlich ist. Diese Kraft bewirkt einen Impulsaustausch innerhalb der Strömung bzw. mit dem Rand, weshalb sie zur Kategorie der Oberflächenkräfte zählt. Kontinuumsströmungen tauschen Impuls über mechanische Spannungen aus, wobei ein Spannungsanstieg eine Beschleunigung bewirkt. Im Kontinuum lässt sich die beschleunigende Kraft in der allgemeinsten Form als Divergenz eines Tensors formulieren:

${\vec {F}}=\nabla \cdot \mathbf {S} =\operatorname {div} \mathbf {S} ,$

wobei ${\mathbf S}$ die Komponente des Spannungstensors auf Grund der Viskosität ist und zäher Spannungstensor oder Reibungstensor heißt. Der Nabla-Operator $\nabla$ bildet hier die Divergenz div des Reibungstensors.

Aus dem Experiment folgt unmittelbar, dass der Reibungstensor eine Funktion der räumlichen Änderung der Strömungsgeschwindigkeit ist:

$\mathbf {S} =\mathbf {S} (\operatorname {grad} {\vec {v}})$

Der Operator grad bildet aus der Geschwindigkeit ${\vec {v}}$ den Geschwindigkeitsgradient. Da kein Impulsfluss bei homogener Strömung $({\vec {v}}={\text{const.}}$ oder $\operatorname {grad} {\vec {v}}=\mathbf {0} ),$ enthält der Reibungstensor keine Komponenten, die unabhängig vom Geschwindigkeitsgefälle sind. In newtonschen Fluiden sind die Spannungen linear in den Geschwindigkeitsgradienten, eine Annahme, die gerechtfertigt ist, wenn der Geschwindigkeitsgradient im Sinne der Hydrodynamik klein ist.

Weiterhin tritt keine Viskosität auf, wenn sich die Strömung in starrer Rotation ( ${\vec {v}}={\vec {\Omega }}\times {\vec {r}}$ mit dem Abstandsvektor ${\vec r}$ von der Drehachse) befindet, wobei ${\vec {\Omega }}$ die Winkelgeschwindigkeit ist, die aus dem schiefsymmetrischen Anteil des Geschwindigkeitsgradienten resultiert, siehe Kinematik in der Strömungsmechanik. Dieser schiefsymmetrische Anteil hat mithin keinen Einfluss auf die Spannungen, weswegen allein der symmetrische Anteil D des Geschwindigkeitsgradienten

$\mathbf {D} :={\frac {1}{2}}[\operatorname {grad} {\vec {v}}+(\operatorname {grad} {\vec {v}})^{\top }]={\frac {1}{2}}{\begin{pmatrix}2{\frac {\partial v_{x}}{\partial x}}&{\frac {\partial v_{x}}{\partial y}}+{\frac {\partial v_{y}}{\partial x}}&{\frac {\partial v_{x}}{\partial z}}+{\frac {\partial v_{z}}{\partial x}}\\&2{\frac {\partial v_{y}}{\partial y}}&{\frac {\partial v_{y}}{\partial z}}+{\frac {\partial v_{z}}{\partial y}}\\{\text{sym.}}&&2{\frac {\partial v_{z}}{\partial z}}\end{pmatrix}}$

Spannungen verursacht. Das hochgestellte T bildet die Transposition. Mit der weiteren Annahme einer isotropen Flüssigkeit werden die unmittelbaren Stoffeigenschaften durch skalare Größen beschrieben. Damit wird der Reibungstensor:

$\mathbf {S} =2\eta \left[\mathbf {D} -{\frac {1}{3}}\operatorname {Sp} (\mathbf {D} )\mathbf {1} \right]+\zeta \operatorname {Sp} (\mathbf {D} )\mathbf {1} \quad {\text{bzw.}}\quad S_{ij}=\eta \left({\frac {\partial v_{i}}{\partial x_{j}}}+{\frac {\partial v_{j}}{\partial x_{i}}}-{\frac {2}{3}}\delta _{ij}\sum _{k=1}^{3}{\frac {\partial v_{k}}{\partial x_{k}}}\right)+\zeta \delta _{ij}\ \sum _{k=1}^{3}{\frac {\partial v_{k}}{\partial x_{k}}}.$

Darin ist $\delta$ das Kronecker-Delta, $\zeta =\lambda +{\tfrac {2}{3}}\eta$ die Volumenviskosität, $\lambda$ die erste Lamé-Konstante, $\operatorname{Sp}$ der Spur-Operator und $\mathbf{1}$ ist der Einheitstensor. Der erste Term beschreibt die Viskosität durch volumentreue Deformation (der Tensor in den eckigen Klammern ist spurfrei oder deviatorisch). Der zweite Term stellt die Viskosität durch Volumenänderung dar. Dieser Term wird bei Inkompressibilität verschwinden, denn dann ist $\operatorname {Sp} (\mathbf {D} )=\operatorname {div} {\vec {v}}=0$ .

Literatur

Peter W. Atkins: Physikalische Chemie / A. Höpfner (Übers.). 3., korr. Auflage. Wiley-VCH, Weinheim 2002, ISBN 3-527-30236-0.
J. M. Dealy: Structure and Rheology of Molten Polymers. Hanser Fachbuchverlag, München 2006.
F. R. Schwarzl: Polymermechanik. Springer, Heidelberg/ Berlin/ New York 1993.

Basierend auf einem Artikel in:

Wikipedia.de