Satz von Pascal

Satz von Pascal in der reellen affinen Ebene: Sind zwei Paare gegenüberliegender Seiten parallel, so auch das dritte Paar

Satz von Pascal

Satz von Pascal: Kanten-Graph

Satz von Pascal: Indizes 2 und 5 vertauscht

Der Satz von Pascal (nach Blaise Pascal) ist eine Aussage über ein 6-Eck auf einem nicht ausgearteten Kegelschnitt in einer projektiven Ebene. Er lässt sich in der reellen affinen Ebene wie folgt formulieren:

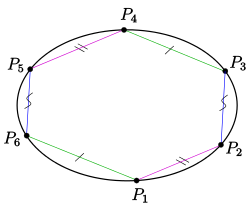
Für ein 6-Eck $P_{1},P_{2},P_{3},P_{4},P_{5},P_{6}$ auf einer Ellipse bei dem zwei Paare gegenüberliegender Seiten parallel sind (im Bild ${\overline {P_{1}P_{2}}}\parallel {\overline {P_{4}P_{5}}},\;{\overline {P_{6}P_{1}}}\parallel {\overline {P_{3}P_{4}}}$ ), ist auch das dritte Paar gegenüberliegender Seiten parallel (im Bild: ${\overline {P_{2}P_{3}}}\parallel {\overline {P_{5}P_{6}}}$ ).

Betrachtet man diesen Satz in dem projektiven Abschluss einer affinen Ebene (man nimmt die "Ferngerade", auf der sich parallele Geraden schneiden, hinzu), so gilt:

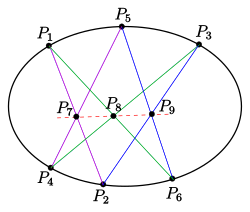
Für beliebige 6 Punkte $P_{1},P_{2},P_{3},P_{4},P_{5},P_{6}$ eines nicht ausgearteten Kegelschnitts in einer projektiven Ebene liegen die Punkte

$P_{7}:=\overline {P_{1}P_{2}}\cap \overline {P_{4}P_{5}},$

$P_{8}:=\overline {P_{6}P_{1}}\cap \overline {P_{3}P_{4}},$

$P_{9}:=\overline {P_{2}P_{3}}\cap \overline {P_{5}P_{6}}$

auf einer Gerade, der Pascal-Gerade (s. Bild).

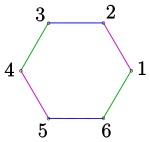
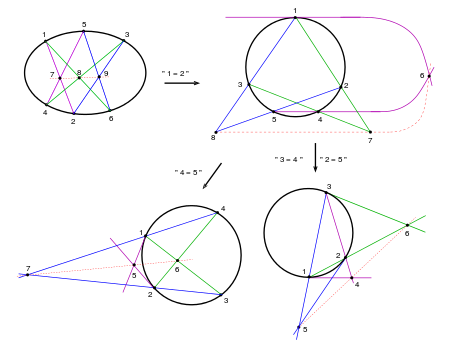
Die Nummerierung gibt an, welche 6 der 15 Verbindungsgeraden der 6 Punkte benutzt werden und welche Kanten benachbart sind. Die Nummerierung ist so gewählt, dass der Kantengraph durch ein reguläres 6-Eck dargestellt werden kann. Geraden zu gegenüberliegenden Kanten des Kantengraphs werden also geschnitten. Sollen andere Kanten in die Pascalfigur eingehen, muss man die Indizes entsprechend permutieren. Für die 2. Pascal-Konfiguration wurden die Indizes 2 und 5 vertauscht (s. Bild, unten).

Nichtausgeartet heißt hier: keine 3 Punkte liegen auf einer Gerade. Den Kegelschnitt kann man sich also als Ellipse vorstellen. (Ein sich schneidendes Geradenpaar ist ein ausgearteter Kegelschnitt.)

Kegelschnitte sind nur in solchen projektiven Ebenen definiert, die sich über (kommutativen) Körpern koordinatisieren lassen. Beispiele von Körpern sind: die reellen Zahlen $\mathbb {R}$ , die rationalen Zahlen $\mathbb {Q}$ , die komplexen Zahlen $\mathbb {C}$ , endliche Körper. Jeder nicht ausgeartete Kegelschnitt einer projektiven Ebene lässt sich in geeigneten homogenen Koordinaten durch die Gleichung $x_{1}x_{2}=x_{0}^{2}$ beschreiben (s. projektiver Kegelschnitt).

Bezug zu anderen Sätzen und Verallgemeinerungen

Satz v.Pascal: Ausartungen

Der Satz von Pascal ist die duale Version des Satzes von Brianchon.
Zum Satz von Pascal gibt es Ausartungen mit 5 bzw. 4 bzw. 3 Punkten (auf einem Kegelschnitt). Bei einer Ausartung fallen zwei durch eine Kante verbundene Punkte formal zusammen und die zugehörige Sekante der Pascalfigur wird durch die Tangente in dem verbleibenden Punkt ersetzt. Siehe hierzu die Figur und weblink planar circlegeometries, S. 30–35. Durch eine geeignete Wahl einer Gerade der Pascalfiguren als Ferngerade ergeben sich Schließungssätze für Hyperbeln und Parabeln. Siehe Hyperbel und Parabel.
Falls der Kegelschnitt vollständig in einer affinen Ebene enthalten ist, gibt es auch (die am Anfang beschriebene) affine Form des Satzes, bei der die Pascalgerade die Ferngerade ist. Die affine Form gibt es z.B. in der reellen und der rationalen affinen Ebene, aber nicht in der komplexen affinen Ebene. In der komplexen projektiven Ebene schneidet jeder n.a. Kegelschnitt jede Gerade. Es gibt also keine Passante des Kegelschnitts, die man als Ferngerade wählen könnte.
Die Figur der sechs Punkte auf dem Kegelschnitt wird auch Hexagrammum Mysticum genannt.
Der Satz von Pascal ist auch für ein Geradenpaar (ausgearteter Kegelschnitt) gültig und ist dann identisch mit dem Satz von Pappos-Pascal.
Der Satz von Pascal wurde durch August Ferdinand Möbius im Jahre 1847 verallgemeinert:

Angenommen, ein Polygon mit 4n+2

Seiten sei in einen Kegelschnitt einbeschrieben. Nun verlängert man die gegenüberliegenden Seiten, bis sie sich in 2n+1

Punkten schneiden. Liegen dann dieser Punkte auf einer gemeinsamen Linie, so liegt auch der letzte Punkt auf dieser Linie.

Eine weitere Verallgemeinerung ist der Satz von Cayley-Bacharach.

Beweis des Satzes von Pascal

Zum Beweis des Satzes von Pascal

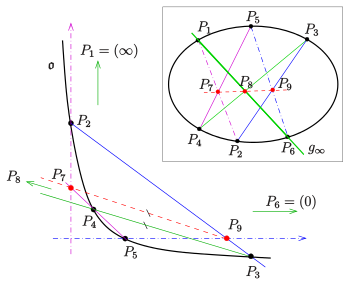
Im reellen Fall kann man den Beweis am Einheitskreis führen. Da ein nichtausgearteter Kegelschnitt über einem beliebigen Körper aber nicht immer als Einheitskreis darstellbar ist, wird hier die immer mögliche Darstellung des Kegelschnitts als Hyperbel benutzt.

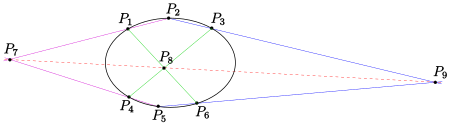
Für den Beweis koordinatisiert man die projektive Ebene inhomogen so, dass $P_{1}=(\infty ),P_{6}=(0)$ ist, d. h. die Ferngerade ist $g_{\infty }={\overline {P_{1}P_{6}}}$ (s. Bild). Ferner sei $P_{5}=(x_{5},0)$ ein Punkt der x-Achse, $P_{2}=(0,y_{2})$ ein Punkt der y-Achse. Dann gilt $P_{9}=(x_{9},0)$ und $P_{7}=(0,y_{7})$ (s. Bild). Die Steigung der Gerade ${\overline {P_{i}P_{k}}}$ sei $m_{ik}$ . Der Satz ist bewiesen, wenn $m_{79}=m_{43}$ bewiesen worden ist.

Man rechnet leicht nach, dass ${\frac {m_{29}}{m_{25}}}={\frac {m_{79}}{m_{75}}}$ ist. Mit $m_{29}=m_{23},\;m_{75}=m_{45}$ (siehe Bild) erhält man

(1) $:\ m_{79}={\frac {m_{23}}{m_{25}}}\cdot m_{45}$ .

Der Kegelschnitt ${\mathfrak {o}}$ wird in dem inhomogenen Koordinatensystem als Hyperbel mit einer Gleichung

$y={\frac {a}{x-b}}+c$ beschrieben (Die Asymptoten sind parallel zu den Koordinatenachsen !).

Für solch eine Hyperbel gilt der Peripheriewinkelsatz für Hyperbeln. Wendet man den Peripheriewinkelsatz auf die Grundpunkte $P_{3},P_{5}$ und die Hyperbelpunkte $P_{2},P_{4}$ an, so erhält man die Gleichung

(2) $:\ {\frac {m_{23}}{m_{25}}}={\frac {m_{43}}{m_{45}}}$ .

Aus (1) und (2) ergibt sich schließlich $m_{79}=m_{43}$ , was zu beweisen war.

Bedeutung des Satzes von Pascal und seiner Ausartungen

Da der Satz von Pascal eine Aussage über Kegelschnitte ist und Kegelschnitte nur in pappusschen Ebenen erklärt sind, führt man den Begriff des Ovals in einer beliebigen projektiven Ebene ein, um die Pascal-Eigenschaft in einer beliebigen projektiven Ebene formulieren zu können. Dies ist z.B. bei dem Satz von Pappus nicht nötig, da dieser ein Satz über Geraden und Punkte ist, die es in jeder projektiven Ebene gibt. Ein Oval ist eine Punktmenge (Kurve) einer projektiven Ebene mit den wesentlichen Inzidenzeigenschaften eines nicht ausgearteten Kegelschnitts.

Definition eines Ovals

→ Hauptartikel: Oval (Projektive Geometrie)

Eine Menge ${\mathfrak {o}}$ von Punkten in einer projektiven Ebene heißt Oval, wenn

(1) Eine beliebige Gerade trifft ${\mathfrak {o}}$ in höchstens 2 Punkten.
Falls $|g\cap {\mathfrak {o}}|=0$ ist, heißt Passante, falls $|g\cap {\mathfrak {o}}|=1$ ist, heißt Tangente und falls $|g\cap {\mathfrak {o}}|=2$ ist, heißt Sekante.

(2) Zu jedem Punkt $P\in {\mathfrak {o}}$ gibt es genau eine Tangente

, d.h. $t\cap {\mathfrak {o}}=\{P\}$ .

Pascal-Eigenschaft eines Ovals

Ein Oval in einer beliebigen projektiven Ebene, das die im Satz von Pascal für Kegelschnitte angegebene Eigenschaft für beliebige 6 Punkte besitzt, nennt mann 6-Punkte-pascalsch oder kurz pascalsch. Entsprechend definiert man 5-Punkte-pascalsch, 4-Punkte-pascalsch und 3-Punkte-pascalsch, falls die Aussage der 5-, 4- oder 3-Punkte-Ausartung des Satzes von Pascal für das Oval erfüllt ist (s. Bild).

Bedeutungen

Die Gültigkeit der Pascal-Eigenschaft oder der 5-Punkte-Ausartung für ein Oval in einer projektiven Ebene hat dieselbe Bedeutung wie die Pappus-Eigenschaft (für ein Geradenpaar):

Satz von Buekenhout

Ist $\mathcal P$ eine projektive Ebene und ${\mathfrak {o}}$ ein $\color{red}6$ -Punkte-pascalsches Oval darin, so ist $\mathcal P$ eine pappussche Ebene und ${\mathfrak {o}}$ ein Kegelschnitt.

Satz von Hofmann,

Ist $\mathcal P$ eine projektive Ebene und ${\mathfrak {o}}$ ein $\color {red}5$ -Punkte-pascalsches Oval darin, so ist $\mathcal P$ eine pappussche Ebene und ${\mathfrak {o}}$ ein Kegelschnitt.

Mit Hilfe der 4-Punkte-Ausartung und der 3-Punkte-Ausartung des Satzes von Pascal lassen sich in pappusschen Ebenen Kegelschnitte charakterisieren:

Satz.: (a): Ist $\mathcal P$ eine pappussche projektive Ebene und ${\mathfrak {o}}$ ein $\color {magenta}4$ -Punkte-pascalsches Oval darin, so ist ${\mathfrak {o}}$ ein Kegelschnitt.; (b): Ist $\mathcal P$ eine pappussche projektive Ebene der Charakteristik $\neq 2$ und ${\mathfrak {o}}$ ein $\color {blue}3$ -Punkte-pascalsches Oval darin, so ist ${\mathfrak {o}}$ ein Kegelschnitt.

Bemerkung: Wie weit man in den beiden letzten Fällen die Voraussetzung pappussch abschwächen kann, ist noch ungeklärt. Die Voraussetzung in Aussage (a) lässt sich mindestens auf moufangsch abschwächen.

Basierend auf einem Artikel in:

Wikipedia.de