Orientierte Fläche

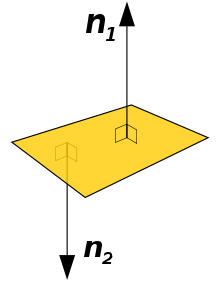
Zwei Normaleneinheitsvektoren einer ebenen Fläche.

Eine orientierte Fläche ist im mathematischen Teilgebiet der elementaren Differentialgeometrie eine orientierbare Fläche, für die festgelegt wurde, welche ihrer zwei Seiten die Außen- bzw. Innenseite ist. Die Orientierung einer Fläche wird mit der Wahl eines der zwei möglichen Flächennormalenvektoren festgelegt. Die Außenseite der Fläche ist diejenige, von der der gewählte Normalenvektor wegführt. Es gibt Flächen, die nicht orientierbar sind, wie zum Beispiel das Möbiusband.

Definition

Eine reguläre Fläche mit einem stetigen Einheitsnormalenfeld

Eine reguläre Fläche (oder eine reguläre Fläche mit Rand) $S\subset \R^3$ heißt orientierbar, falls es ein stetiges Einheitsnormalenvektorfeld auf gibt.

Ein solches stetiges Einheitsnormalenvektorfeld ${\vec {n}}$ auf legt eine Orientierung von fest. Eine orientierte Fläche ist somit eine orientierbare Fläche, auf der ein stetiges Einheitsnormalenvektorfeld ${\vec {n}}$ ausgewählt wurde. Formal ist eine orientierte Fläche ein Paar $(S,\vec n)$ aus einer orientierbaren Fläche und einem stetigen Einheitsnormalenvektorfeld ${\vec {n}}$ auf .

Ist durch das stetige Einheitsnormalenvektorfeld ${\vec {n}}_{1}$ eine Orientierung auf der Fläche gegeben, so ist auch $\vec n_2 = - \vec n_1$ ein stetiges Einheitsnormalenvektorfeld, das eine weitere Orientierung von definiert. Ist die orientierbare Fläche zusammenhängend, so gibt es genau diese zwei Orientierungen. Besteht die Fläche aus mehreren Zusammenhangskomponenten, so kann auf jeder Zusammenhangskomponente eine Orientierung unabhängig von den andern gewählt werden.

Ist auf einer Fläche eine Orientierung ausgewählt, so wird diese als positiv bezeichnet, die entgegengesetzte Orientierung als negativ.

Anschauung

Geschlossene Flächen

Eine zusammenhängende geschlossene Fläche, wie zum Beispiel eine Sphäre (Kugeloberfläche) oder ein Torus, zerlegt den Raum in zwei zusammenhängende Teile, das Innere und das Äußere. Entsprechend spricht man von der Innen- und der Außenseite der Fläche. Einer Auswahl der Außenseite entspricht ein nach außen weisendes, einer Auswahl der Innenseite ein nach innen weisendes Einheitsnormalenvektorfeld. Wenn nichts anderes gesagt wird, dann wählt man die Orientierung durch ein nach außen weisendes Einheitsnormalenvektorfeld. Für die Anwendung des Gaußschen Integralsatzes wird dies vorausgesetzt.

Flächen mit Rand

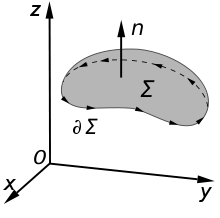
Eine orientierte Fläche mit Rand und der zugehörige Durchlaufsinn ihrer Randkurve.

Bei Flächen mit Rand wird durch eine Orientierung der Fläche eine Orientierung (Durchlaufsinn) der Randkurve(n) festgelegt.

Anschaulich: Betrachtet man die ausgewählte Seite der Fläche als „oben“ und stellt man sich einen Beobachter vor, der auf der Oberseite der Fläche längs des Randes so geht, dass die Fläche links von ihm liegt, so durchläuft der Beobachter die Kurve in positiver Richtung. Man sagt, dass der Umlaufsinn der Randkurve mit der Flächennormale eine Rechtsschraube oder Rechtsschraubung bildet, da eine zur Flächennormale parallele Rechtsschraube bei Drehung im Rand-Umlaufsinn in Richtung der Flächennormale vorrücken würde. Wird die Fläche durch eine einzige Randkurve begrenzt, so bestimmt umgekehrt ein Durchlaufsinn der Randkurve eine Orientierung der Fläche.

Beim klassischen Integralsatz von Stokes wird vorausgesetzt, dass die Orientierung der Fläche und der Durchlaufsinn der Randkurve(n) auf die genannte Art zusammenhängen.

Orientierte Ebenen

Eine Ebene im dreidimensionalen Raum $\mathbb {R} ^{3}$ zerlegt diesen in einen positiven und negativen Halbraum, wobei als Orientierung der Ebene (bis auf den undefinierten Sonderfall der Ursprungsebene) diejenige gewählt wird, bei der der Koordinatenursprung im negativen Halbraum liegt, der Normalenvektor der Ebene also in Richtung des positiven Halbraums zeigt.

Orientierte Ebenen spielen z.B. bei Abstandsberechnungen mit Hilfe der Hesseschen Normalform der vektoriellen Ebenengleichung eine Rolle.

Verallgemeinert man die Vorstellung der Ebene im dreidimensionalen Raum $\mathbb {R} ^{3}$ zu der der Hyperebene im n-dimensionalen Raum $\mathbb {R} ^{n}$ , lässt sich analog auch mit orientierten Hyperebenen höherer oder niederer Dimension rechnen. Im zweidimensionalen Raum $\mathbb {R} ^{2}$ etwa ist dies eine orientierte Gerade, die den Raum $\mathbb {R} ^{2}$ in zwei Halbebenen teilt, wobei der Normalenvektor der Gerade auch in diesem Fall per Definition in den positiven Halbraum (hier die positive Halbebene) zeigt, also (vom undefinierten Sonderfall der Ursprungsgerade abgesehen) auch hier vom Koordinatenursprung weg. Hyperebenen höherer Dimension dagegen finden z.B. bei der Lösung bestimmter wirtschaftsmathematischer Fragen Anwendung.

Relevanz in der Physik und Mathematik

Die Vereinbarung der Orientierung einer Fläche ist insbesondere bei der Berechnung von vektoriellen Oberflächenintegralen von großer Bedeutung, z.B. in der Elektrostatik bei der Verwendung des Gaußschen Integralsatzes. Die Orientierung bestimmt das Vorzeichen des Ergebnisses. Möchte man z.B. die Ladung Q innerhalb eines vorgegebenen Volumens berechnen und es ist nur das elektrische Feld $\vec E(\vec x)$ auf der Oberfläche des Volumens bekannt, so kann man mit Hilfe dieses Satzes auf die eingeschlossene Ladung schließen.

$Q=\int_V\mathrm{d}V\varrho(\vec x) =\varepsilon_0\int_V \mathrm{d}V\mathrm{div}\vec{E}(\vec x)$ .

Hier ist V das Volumen, in dem die unbekannte Ladung enthalten ist, und $\varrho$ die unbekannte Ladungsdichte. Mit Hilfe der ersten Maxwellgleichung kommt man auf den Ausdruck auf der rechten Seite, mit $\varepsilon _{0}$ der Dielektrizitätskonstanten und div der Divergenz. Mithilfe des Gaußschen Integralsatzes kann nun das Volumenintegral in ein Oberflächenintegral umformuliert werden:

$Q=\varepsilon_0\int_{\partial V} \mathrm{d}\vec A\cdot\vec{E}(\vec x)$ .

$\mathrm{d}\vec A$ ist ein infinitesimales orientiertes Flächenelement der Oberfläche $\partial V$ des Volumens. Das Vorzeichen des Skalarproduktes $\mathrm{d}\vec A\cdot\vec{E}$ hängt von der Richtung von $\mathrm{d}\vec A$ ab. Ist $\mathrm{d}\vec A$ parallel zu ${\vec {E}}$ , so ist das Skalarprodukt $\mathrm{d}A\,E$ , sind dagegen beide Vektoren antiparallel so ist das Skalarprodukt $-\mathrm{d}A\,E$ . Somit hängt das Vorzeichen des Oberflächenintegrals von der gewählten Orientierung der Oberfläche ab. Als Konvention wurde die Wahl einer positiven Orientierung vereinbart, das heißt man wählt das nach außen weisende Einheitsnormalenvektorfeld (siehe oben) als Orientierung einer Fläche.

Basierend auf einem Artikel in:

Wikipedia.de