
Skalarprodukt
Das Skalarprodukt (auch inneres Produkt oder
Punktprodukt) ist eine mathematische
Verknüpfung, die zwei Vektoren
eine Zahl (Skalar)
zuordnet. Es ist Gegenstand der analytischen
Geometrie und der linearen
Algebra. Historisch wurde es zuerst im euklidischen
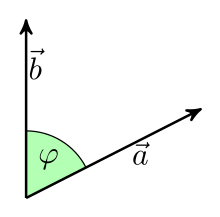
Raum eingeführt. Geometrisch berechnet man das Skalarprodukt zweier Vektoren
und
nach der Formel
Dabei bezeichnen
und
jeweils die Längen
(Beträge) der Vektoren. Mit
wird der Kosinus
des von den beiden Vektoren eingeschlossenen Winkels
bezeichnet. Das Skalarprodukt zweier Vektoren gegebener Länge ist damit null,
wenn sie senkrecht
zueinander stehen, und maximal, wenn sie die gleiche Richtung haben.
In einem kartesischen
Koordinatensystem berechnet sich das Skalarprodukt zweier Vektoren
und
als
Kennt man die kartesischen Koordinaten der Vektoren, so kann man mit dieser
Formel das Skalarprodukt und daraufhin mit der Formel aus dem vorhergehenden
Absatz den Winkel
zwischen den beiden Vektoren ausrechnen, indem diese nach
aufgelöst wird:
In der linearen Algebra wird dieses Konzept verallgemeinert. Ein Skalarprodukt ist dort eine Funktion, die zwei Elementen eines reellen oder komplexen Vektorraums einen Skalar zuordnet, genauer eine (positiv definite) hermitesche Sesquilinearform, bzw. spezieller bei reellen Vektorräumen eine (positiv definite) symmetrische Bilinearform. Im Allgemeinen ist in einem Vektorraum von vornherein kein Skalarprodukt festgelegt. Ein Raum zusammen mit einem Skalarprodukt wird als Innenproduktraum oder Prähilbertraum bezeichnet. Diese Vektorräume verallgemeinern den euklidischen Raum und ermöglichen damit die Anwendung geometrischer Methoden auf abstrakte Strukturen.
Im euklidischen Raum
Geometrische Definition und Notation
Vektoren im dreidimensionalen euklidischen
Raum oder in der zweidimensionalen euklidischen Ebene kann man als Pfeile
darstellen. Dabei stellen Pfeile, die parallel,
gleich lang und gleich orientiert sind, denselben Vektor dar. Das Skalarprodukt
zweier Vektoren
und
ist ein Skalar, das heißt eine reelle Zahl. Geometrisch lässt es sich wie folgt
definieren:
Bezeichnen
und
die Längen der Vektoren
und
und bezeichnet
den von
und
eingeschlossenen Winkel, so ist
Wie bei der normalen Multiplikation (aber seltener als dort) wird, wenn klar ist, was gemeint ist, das Multiplikationszeichen manchmal weggelassen:
Statt
schreibt man in diesem Fall gelegentlich auch
Andere übliche Notationen sind
und
Veranschaulichung
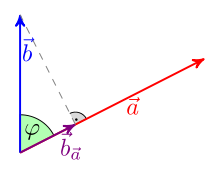
Um sich die Definition zu veranschaulichen, betrachtet man die orthogonale
Projektion
des Vektors
auf die durch
bestimmte Richtung und setzt
Es gilt dann
und für das Skalarprodukt von
und
gilt:
Diese Beziehung wird manchmal auch zur Definition des Skalarprodukts verwendet.
Beispiele
In allen drei Beispielen gilt
und
.
Die Skalarprodukte ergeben sich mithilfe der speziellen Kosinuswerte
,
und
:
-
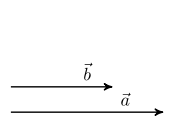
und
gleichgerichtet
-
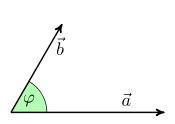
und
im 60°-Winkel
-

und
orthogonal
In kartesischen Koordinaten
Führt man in der euklidischen Ebene bzw. im euklidischen Raum kartesische Koordinaten ein, so besitzt jeder Vektor eine Koordinatendarstellung als 2- bzw. 3-Tupel, das meist als Spalte geschrieben wird.
In der euklidischen Ebene erhält man dann für das Skalarprodukt der Vektoren
und
die Darstellung
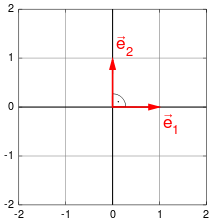
Für die kanonischen
Einheitsvektoren
und
gilt nämlich:
und
Daraus folgt (unter Vorwegnahme der weiter unten erläuterten Eigenschaften des Skalarproduktes):
Im dreidimensionalen euklidischen Raum erhält man entsprechend für die Vektoren
und
die Darstellung
Zum Beispiel berechnet sich das Skalarprodukt der beiden Vektoren
und
wie folgt:
Eigenschaften
Aus der geometrischen Definition ergibt sich direkt:
- Sind
und
parallel und gleichorientiert (
), so gilt
- Insbesondere ergibt das Skalarprodukt eines Vektors mit sich selbst das
Quadrat seiner Länge:
- Sind
und
parallel und entgegengesetzt orientiert (
), so gilt
- Sind
und
orthogonal (
), so gilt
- Ist
ein spitzer Winkel, so gilt
- Ist
ein stumpfer Winkel, so gilt
Als Funktion, die jedem geordneten Paar
von Vektoren die reelle Zahl
zuordnet, hat das Skalarprodukt folgende Eigenschaften, die man von einer
Multiplikation erwartet:
- Es ist symmetrisch
(Kommutativgesetz):
für alle Vektoren
und
- Es ist homogen
in jedem Argument (gemischtes Assoziativgesetz):
für alle Vektoren
und
und alle Skalare
- Es ist additiv
in jedem Argument (Distributivgesetz):
und
für alle Vektoren
und
Die Eigenschaften 2 und 3 fasst man auch zusammen zu: Das Skalarprodukt ist bilinear.
Die Bezeichnung „gemischtes Assoziativgesetz“ für die 2. Eigenschaft
verdeutlicht, dass dabei ein Skalar und zwei Vektoren so verknüpft werden, dass
die Klammern wie beim Assoziativgesetz vertauscht werden können. Da das
Skalarprodukt keine innere Verknüpfung ist, ist ein Skalarprodukt von
drei Vektoren nicht definiert, daher stellt sich die Frage nach einer echten
Assoziativität nicht. Im Ausdruck
ist nur die erste Multiplikation ein Skalarprodukt von zwei Vektoren, die zweite
ist das Produkt eines Skalars mit einem Vektor (S-Multiplikation).
Der Ausdruck stellt einen Vektor dar, ein Vielfaches des Vektors
Hingegen stellt der Ausdruck
ein Vielfaches von
dar. Im Allgemeinen gilt also
Weder die geometrische Definition noch die Definition in kartesischen Koordinaten ist willkürlich. Beide folgen aus der geometrisch motivierten Forderung, dass das Skalarprodukt eines Vektors mit sich selbst das Quadrat seiner Länge ist, und der algebraisch motivierten Forderung, dass das Skalarprodukt die obigen Eigenschaften 1–3 erfüllt.
Betrag von Vektoren und eingeschlossener Winkel
Mit Hilfe des Skalarproduktes ist es möglich, aus der Koordinatendarstellung die Länge (den Betrag) eines Vektors zu berechnen:
Für einen Vektor
des zweidimensionalen Raumes gilt
Man erkennt hier den Satz des Pythagoras wieder. Im dreidimensionalen Raum gilt entsprechend
Indem man die geometrische Definition mit der Koordinatendarstellung kombiniert, kann man aus den Koordinaten zweier Vektoren den von ihnen eingeschlossenen Winkel berechnen. Aus
folgt
Die Längen der beiden Vektoren
und
betragen also
und
Der Kosinus des von den beiden Vektoren eingeschlossenen Winkels berechnet sich zu
Somit ist
Orthogonalität und orthogonale Projektion

Zwei Vektoren
und
sind genau dann orthogonal, wenn ihr Skalarprodukt null ist, also
Die orthogonale Projektion von
auf die durch den Vektor
gegebene Richtung ist der Vektor
mit
also
Die Projektion ist der Vektor, dessen Endpunkt der Lotfußpunkt vom Endpunkt
von
auf die durch
bestimmte Gerade durch den Nullpunkt ist. Der Vektor
steht senkrecht auf
Ist
ein Einheitsvektor
(d.h., ist
),
so vereinfacht sich die Formel zu
Bezug zum Kreuzprodukt
Eine andere Art und Weise, zwei Vektoren
und
im dreidimensionalen Raum multiplikativ miteinander zu verknüpfen, ist das
äußere Produkt oder Kreuzprodukt
Im Gegensatz zum Skalarprodukt ist das Resultat des Kreuzprodukts kein Skalar,
sondern wieder ein Vektor. Dieser Vektor steht senkrecht
auf der von den beiden Vektoren
und
aufgespannten Ebene
und seine Länge entspricht dem Flächeninhalt
des Parallelogramms,
das von diesen aufgespannt wird.
Für die Verbindung von Kreuz- und Skalarprodukt gelten die folgenden Rechenregeln:
Die Kombination aus Kreuzprodukt und Skalarprodukt der ersten beiden Regeln
nennt man auch Spatprodukt;
es ergibt das orientierte
Volumen des
durch die drei Vektoren
aufgespannten Parallelepipeds.
Anwendungen
In der Geometrie
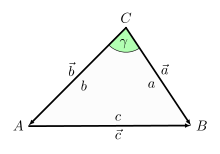
Das Skalarprodukt ermöglicht es, komplizierte Sätze, bei denen von Winkeln die Rede ist, einfach zu beweisen.
Behauptung: (Kosinussatz)
Beweis: Mit Hilfe der eingezeichneten Vektoren folgt
(Die Richtung von
ist unerheblich.) Quadrieren des Betrags ergibt
und damit
In der Physik
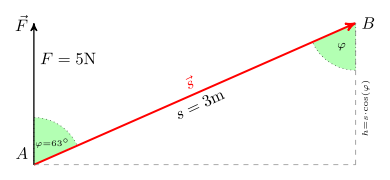
In der Physik sind viele Größen,
wie zum Beispiel die Arbeit
,
durch Skalarprodukte definiert:
mit den vektoriellen Größen Kraft
und Weg
.
Dabei bezeichnet
den Winkel zwischen der Richtung der Kraft und der Richtung des Weges. Mit
wird die Komponente der Kraft in Richtung des Weges bezeichnet, mit
die Komponente des Weges in Richtung der Kraft.
Beispiel: Ein Wagen des Gewichts
wird über eine schiefe Ebene von
nach
transportiert. Die Hubarbeit
berechnet sich zu
In allgemeinen reellen und komplexen Vektorräumen
Man nimmt die obigen Eigenschaften zum Anlass, den Begriff des Skalarprodukts auf beliebige reelle und komplexe Vektorräume zu verallgemeinern. Ein Skalarprodukt ist dann eine Funktion, die zwei Vektoren ein Körperelement (Skalar) zuordnet und die genannten Eigenschaften erfüllt. Im komplexen Fall modifiziert man dabei die Bedingung der Symmetrie und der Bilinearität, um die Positivdefinitheit zu retten (die für komplexe symmetrische Bilinearformen nie erfüllt ist).
In der allgemeinen Theorie werden die Variablen für Vektoren, also Elemente
eines beliebigen Vektorraums, im Allgemeinen nicht durch Pfeile gekennzeichnet.
Das Skalarprodukt wird meist nicht durch einen Malpunkt, sondern durch ein Paar
von spitzen Klammern bezeichnet. Für das Skalarprodukt der Vektoren
und
schreibt man also
.
Andere gebräuchliche Notationen sind
(vor allem in der Quantenmechanik
in Form der Bra-Ket-Notation),
und
.
Definition (Axiomatik)
Ein Skalarprodukt oder inneres Produkt auf einem reellen
Vektorraum
ist eine positiv definite symmetrische Bilinearform
das heißt, für
und
gelten die folgenden Bedingungen:
- linear in jedem der beiden Argumente:
- symmetrisch:
- positiv definit:
genau dann, wenn
Ein Skalarprodukt oder inneres Produkt auf einem komplexen Vektorraum
ist eine positiv
definite hermitesche
Sesquilinearform
das heißt für
und
gelten die folgenden Bedingungen:
- sesquilinear:
(semilinear im ersten Argument)
(linear im zweiten Argument)
- hermitesch:
- positiv definit:
(Dass
reell ist, folgt aus Bedingung 2.)
genau dann, wenn
Ein reeller oder komplexer Vektorraum, in dem ein Skalarprodukt definiert
ist, heißt Skalarproduktraum oder Prähilbertraum.
Ein endlichdimensionaler reeller Vektorraum mit Skalarprodukt wird auch
euklidischer Vektorraum genannt, im komplexen Fall spricht man von einem
unitären Vektorraum. Entsprechend wird das Skalarprodukt in einem
euklidischen Vektorraum gelegentlich als euklidisches Skalarprodukt, das
in einem unitären Vektorraum als unitäres Skalarprodukt bezeichnet. Die
Bezeichnung „euklidisches Skalarprodukt“ wird aber auch speziell für das oben
beschriebene geometrische Skalarprodukt oder das weiter unten beschriebene Standardskalarprodukt
im
benutzt.
- Anmerkungen
- Oft wird jede symmetrische Bilinearform bzw. jede hermitesche Sesquilinearform als Skalarprodukt bezeichnet; mit diesem Sprachgebrauch beschreiben die obigen Definitionen positiv definite Skalarprodukte.
- Die beiden angegebenen Axiomensysteme sind nicht minimal. Im reellen Fall folgt aufgrund der Symmetrie die Linearität im ersten Argument aus der Linearität im zweiten Argument (und umgekehrt). Analog dazu folgt im komplexen Fall aufgrund der Hermitezität die Semilinearität im ersten Argument aus der Linearität im zweiten Argument (und umgekehrt).
- Im komplexen Fall wird das Skalarprodukt manchmal alternativ, nämlich als
linear im ersten und semilinear im zweiten Argument definiert. Diese Version
tritt bevorzugt in der Mathematik und insbesondere in der Analysis auf, während in der
Physik überwiegend die obige Version benutzt wird (siehe Bra- und
Ket-Vektoren). Der Unterschied beider Versionen liegt in den Auswirkungen
der Skalarmultiplikation
hinsichtlich der Homogenität.
Nach der Alternativversion gilt für
und
und
. Die Additivität wird in beiden Versionen gleich verstanden. Ebenso sind die nach beiden Versionen aus dem Skalarprodukt gewonnenen Normen identisch.
- Ein Prähilbertraum, der vollständig bezüglich der durch das Skalarprodukt induzierten Norm ist, wird als Hilbertraum bezeichnet.
- Die Unterscheidung zwischen reellem und komplexem Vektorraum bei der Definition des Skalarprodukts ist nicht zwingend notwendig, da eine hermitesche Sesquilinearform im Reellen einer symmetrischen Bilinearform entspricht.
Beispiele
Standardskalarprodukt im Rn und im Cn
Ausgehend von der Darstellung des euklidischen Skalarprodukts in kartesischen
Koordinaten definiert man in der linearen
Algebra das Standardskalarprodukt im -dimensionalen
Koordinatenraum
für
durch
Das oben behandelte „geometrische“ Skalarprodukt im euklidischen Raum
entspricht so dem Spezialfall
Im Fall des
-dimensionalen
komplexen Vektorraums
definiert man das Standardskalarprodukt für
durch
wobei der Überstrich die komplexe Konjugation bedeutet. In der Mathematik ist häufig auch die alternative Version gebräuchlich, bei der das zweite Argument statt des ersten konjugiert wird.
Das Standardskalarprodukt im
bzw.
lässt sich auch als Matrizenprodukt
schreiben, indem man den Vektor als
-Matrix
(Spaltenvektor)
interpretiert: Im reellen Fall gilt
wobei
der Zeilenvektor
ist, der aus dem Spaltenvektor
durch Transponieren
hervorgeht. Im komplexen Fall gilt (für den links semilinearen, rechts linearen
Fall)
wobei
der zu
hermitesch
adjungierte Zeilenvektor ist.
Allgemeine Skalarprodukte im Rn und im Cn
Allgemeiner definiert im reellen Fall jede symmetrische und positiv
definite Matrix
über
ein Skalarprodukt; ebenso wird im komplexen Fall für jede positiv definite hermitesche
Matrix
über
ein Skalarprodukt definiert. Hier bezeichnen die spitzen Klammern auf der
rechten Seite das Standardskalarprodukt, die spitzen Klammern mit dem Index
auf der linken Seite das durch die Matrix
definierte Skalarprodukt.
Jedes Skalarprodukt auf
bzw.
lässt sich auf diese Art durch eine positiv definite symmetrische Matrix (bzw.
positiv definite hermitesche Matrix) darstellen.
L2-Skalarprodukt für Funktionen
Auf dem unendlichdimensionalen Vektorraum
der stetigen
reellwertigen Funktionen
auf dem Intervall
ist das
-Skalarprodukt
durch
für alle
definiert.
Für Verallgemeinerungen dieses Beispiels siehe Prähilbertraum und Hilbertraum.
Frobenius-Skalarprodukt für Matrizen
Auf dem Matrizenraum
der reellen
-Matrizen
wird für
durch
ein Skalarprodukt definiert. Entsprechend wird auf dem Raum
der komplexen
-Matrizen
für
durch
ein Skalarprodukt definiert. Dieses Skalarprodukt wird Frobenius-Skalarprodukt genannt und die dazugehörige Norm heißt Frobeniusnorm.
Norm, Winkel und Orthogonalität
Der Länge eines Vektors im euklidischen Raum entspricht in allgemeinen Skalarprodukträumen die vom Skalarprodukt induzierte Norm. Man definiert diese Norm, indem man die Formel für die Länge aus dem euklidischen Raum überträgt, als die Wurzel des Skalarprodukts des Vektors mit sich selbst:
Dies ist möglich, da
aufgrund der positiven Definitheit nicht negativ ist. Die als Normaxiom
geforderte Dreiecksungleichung
folgt dabei aus der Cauchy-Schwarzschen
Ungleichung
Sind
so kann diese Ungleichung zu
umgeformt werden. Daher lässt sich auch in allgemeinen reellen Vektorräumen mittels
der Winkel
zweier Vektoren definieren. Der so definierte Winkel liegt zwischen 0° und 180°,
also zwischen 0 und
Für Winkel zwischen komplexen Vektoren gibt es eine Reihe unterschiedlicher
Definitionen.
Auch im allgemeinen Fall nennt man Vektoren, deren Skalarprodukt gleich Null ist, orthogonal:
Matrixdarstellung
Ist
ein
-dimensionaler
Vektorraum und
eine Basis
von
so kann jedes Skalarprodukt
auf
durch eine (
)-Matrix
die Gramsche
Matrix des Skalarprodukts, beschrieben werden. Ihre Einträge sind die
Skalarprodukte der Basisvektoren:
mit
für
Das Skalarprodukt lässt sich dann mit Hilfe der Basis darstellen: Haben die
Vektoren
bezüglich der Basis
die Darstellung
und
so gilt im reellen Fall
Bezeichnet man mit
die Koordinatenvektoren
und
so gilt also
wobei das Matrixprodukt
eine -Matrix
liefert, also eine reelle Zahl. Mit
wird der Zeilenvektor
bezeichnet, der durch Transponieren
aus dem Spaltenvektor
entsteht.
Im komplexen Fall gilt entsprechend
wobei der Überstrich komplexe
Konjugation bezeichnet und
der zu
adjungierte
Zeilenvektor ist.
Ist
eine Orthonormalbasis,
das heißt, gilt
für alle
und
für alle
so ist
die Einheitsmatrix,
und es gilt
im reellen Fall und
im komplexen Fall. Bezüglich einer Orthonormalbasis entspricht das
Skalarprodukt von
und
also dem Standardskalarprodukt
der Koordinatenvektoren
und
bzw.
Siehe auch
Literatur
- Gerd Fischer: Lineare Algebra. 15. Auflage. Vieweg Verlag, ISBN 3-528-03217-0.
- Walter Rudin: Reelle und komplexe Analysis. 2. verbesserte Auflage. Oldenbourg Wissenschaftsverlag, München 2009, ISBN 978-3-486-59186-6.
Anmerkung
- ↑
Gleichbedeutend mit:


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 06.05. 2021