Dreieck
Ein Dreieck (veraltet auch Triangel, lateinisch: triangulum) ist ein Polygon und eine geometrische Figur. Es handelt sich innerhalb der euklidischen Geometrie um die einfachste Figur in der Ebene, die von geraden Linien begrenzt wird. Seine Begrenzungslinien bezeichnet man als Seiten. In seinem Inneren spannen sich drei Winkel, die sogenannten Innenwinkel auf. Die Scheitel dieser Winkel bezeichnet man als Eckpunkte des Dreiecks. Auch eine Verallgemeinerung des Dreiecksbegriffes auf nichteuklidische Geometrien ist möglich. In diesem Fall müssen die Begrenzungslinien Geodäten sein.
In der Trigonometrie, einem Teilgebiet der Mathematik, spielen Dreiecke die wesentliche Rolle.
Einteilung
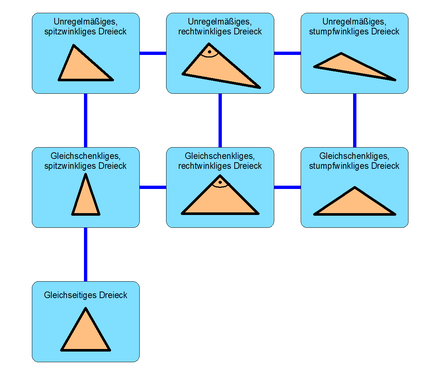
Von links nach rechts: spitzwinklig, rechtwinklig, stumpfwinklig
Von oben nach unten: unregelmäßig, gleichschenklig, gleichseitig
Nach Seitenlängen
Nach Winkeln
Spitz- und stumpfwinklige Dreiecke werden auch unter dem Namen schiefwinkliges Dreieck zusammengefasst.
Das allgemeine Dreieck
Definition und Eigenschaften
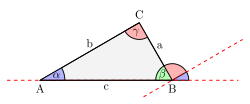
Ein Dreieck wird durch drei Punkte definiert, die nicht auf einer Geraden liegen. Sie werden Ecken des Dreiecks genannt. Die Verbindungsstrecken zwischen je zwei Ecken heißen Seiten des Dreiecks. Das Dreieck unterteilt die Ebene in zwei Bereiche, das Äußere und das Innere des Dreiecks. Der von je zwei an einem Eckpunkt zusammentreffenden Seiten gebildete Winkel ist eine wichtige Größe zur Charakterisierung des Dreiecks.
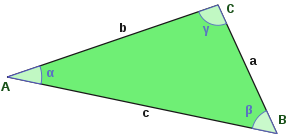
In der Geometrie werden die Eckpunkte
des Dreiecks in der Regel mit ,
und
bezeichnet, üblicherweise so wie abgebildet, gegen den Uhrzeigersinn. Die Seite,
die einer Ecke gegenüberliegt, wird analog
,
bzw.
genannt. Damit liegt z.B. die Seite
dem Eckpunkt
gegenüber, verbindet also die Punkte
und
.
Häufig wird mit
,
und
auch stattdessen die Länge der jeweiligen Seite
,
oder
bezeichnet. Die Winkel werden
,
und
genannt.
ist der Winkel am Eckpunkt
,
liegt am Eckpunkt
und
liegt am Eckpunkt
- Die Summe der Innenwinkel in einem planaren (ebenen) Dreieck beträgt immer 180°.
- Die Summe der Außenwinkel beträgt entsprechend 360°. Dabei wird für jeden Eckpunkt nur ein Außenwinkel in die Summe aufgenommen. Da es sich bei den beiden Außenwinkeln eines Eckpunktes um Scheitelwinkel handelt, sind diese immer gleich groß. Die Summe aller Außenwinkel beträgt demnach genau genommen 2 · 360° = 720°.
- Die Gesamtlänge zweier Seiten eines Dreiecks ist mindestens so groß wie die Länge der dritten Seite. Diese Beziehungen lassen sich in der so genannten Dreiecksungleichung ausdrücken.
Diese intuitiv einsichtigen Eigenschaften ebener Dreiecke folgen aus den Axiomen der euklidischen Geometrie.
Ausgezeichnete Kreise, Geraden und Punkte
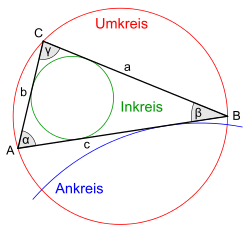
Jedes Dreieck besitzt einen Umkreis, das heißt einen Kreis, der durch seine drei Eckpunkte verläuft. Der Mittelpunkt des Umkreises ist der Schnittpunkt der drei Mittelsenkrechten. Das sind die Lotgeraden durch die Mittelpunkte der Seiten.
Die Winkelhalbierenden der drei Innenwinkel schneiden sich ebenfalls in einem gemeinsamen Punkt, nämlich im Mittelpunkt des Inkreises. Dieser berührt die drei Seiten von innen. Die drei Kreise, die jeweils eine Seite von außen und die Verlängerungen der beiden anderen Seiten berühren, heißen Ankreise des Dreiecks.
Der Schwerpunkt eines Dreiecks ist der gemeinsame Schnittpunkt der drei Seitenhalbierenden, also der jeweiligen Verbindungsstrecken der Eckpunkte mit dem Mittelpunkt der gegenüberliegenden Seite. Der Schwerpunkt teilt dabei die Seitenhalbierenden im Verhältnis 2:1.
Auch die drei Höhen, also die Lote der Eckpunkte auf die jeweils gegenüberliegende Seite, schneiden sich in einem gemeinsamen Punkt, dem Höhenschnittpunkt. Mit Hilfe der Höhen kann der Flächeninhalt eines Dreiecks berechnet werden (siehe Dreiecksfläche).
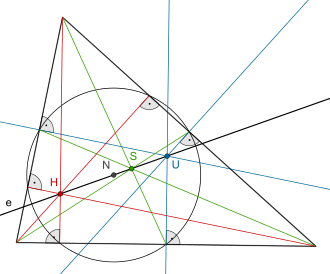
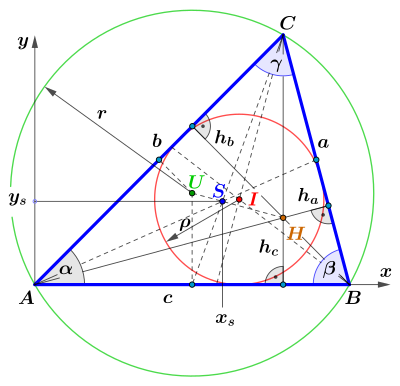
Höhenschnittpunkt H (rot),
Schwerpunkt S (grün, Schnittpunkt der Seitenhalbierenden),
Umkreismittelpunkt U (blau, Schnittpunkt der Mittelsenkrechten),
Feuerbachkreis mit Mittelpunkt N (schwarz)
Ein weiterer bekannter Kreis am Dreieck ist der Feuerbachkreis. Er wird auch Neunpunktekreis genannt, da er durch die drei Seitenmittelpunkte, die drei Fußpunkte der Höhen und die drei Mittelpunkte der oberen Höhenabschnitte verläuft. Sein Mittelpunkt liegt wie der Schwerpunkt, der Umkreismittelpunkt und der Höhenschnittpunkt auf der eulerschen Geraden.
Berechnung eines beliebigen Dreiecks
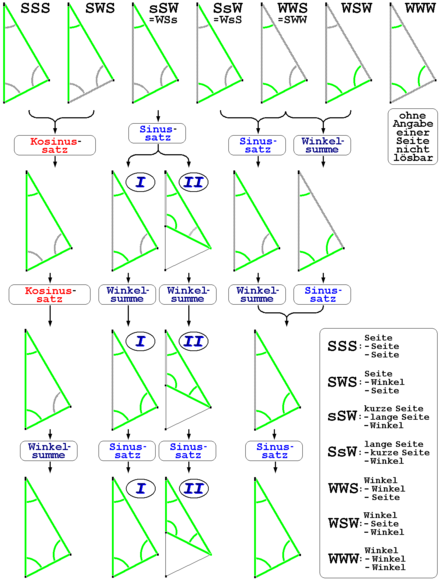
Ein Dreieck besitzt drei Seiten und drei Innenwinkel. Liegen drei Angaben zur Größe dieser Seiten oder Winkel vor, kann man daraus die jeweils fehlenden übrigen Seiten oder Winkel berechnen, es sei denn, es sind nur die drei Winkel gegeben.
Je nachdem, welche Kombination bekannter Seiten und/oder Winkel dabei im Einzelnen gegeben ist, ist das Ergebnis entweder ein- oder mehrdeutig (siehe nebenstehende Abb.).
So liefern die Kongruenzsätze zunächst einmal drei stets eindeutig lösbare Konstellationen, die man symbolisch mit SSS, SWS und WSW bezeichnet, wobei S für eine bekannte Seite und W für einen bekannten Winkel steht.
SSW- oder WSS-Fall
Der SSW- oder WSS-Fall dagegen ist nur dann eindeutig, wenn der bekannte Winkel der größeren der beiden gegebenen Seiten gegenüberliegt (SsW-Fall) – liegt er der kleineren Seite gegenüber (sSW-Fall), gibt es meist zwei verschiedene Dreiecke, die die Ausgangsbedingungen erfüllen. Dies allerdings muss nicht immer so sein, wie der Sonderfall mit dem Seitenverhältnis 1:2 und dem Winkel 30° zeigt, bei dem es genau dann gleichwohl nur ein so bestimmtes Dreieck gibt, wenn der Winkel gegenüber der längeren Seite 90° beträgt. Zu erwähnen ist schließlich die rein rechnerisch mögliche Situation, dass gar kein Dreieck die Ausgangsbedingungen erfüllt, nämlich dann, wenn sich für den Sinus des der längeren Seite gegenüberliegenden Winkels ein Wert > 1 ergibt (bei real existierenden Dreiecken allerdings ist dieser Fall naturgemäß ausgeschlossen).
WWS- oder SWW-Fall
Der WWS- oder SWW-Fall kann (wie nebenstehender Abbildung zu entnehmen) auf zweierlei Weise gelöst werden: Entweder man berechnet mittels des Sinussatzes zunächst einmal eine der beiden noch fehlenden Seiten und rechnet dann weiter wie im SSW-Fall, oder aber man bestimmt, was wesentlich bequemer ist, mittels der Winkelsumme im Dreieck den noch fehlenden dritten Winkel und verfährt dann weiter wie im WSW-Fall.
SSS-Fall
Wenn die größte der drei Seiten kleiner als die Summe der beiden anderen Seiten ist, dann ist das Dreieck (bis auf Kongruenz) eindeutig bestimmt. Ansonsten gibt es kein Dreieck mit den vorgegebenen drei Seiten. Die Innenwinkel des Dreiecks lassen sich z.B. mit dem Kosinussatz berechnen.
WWW-Fall
Der WWW-Fall ist bei ebenen Dreiecken überhaupt nicht eindeutig lösbar, weil in diesem Fall in Wirklichkeit nur zwei voneinander unabhängige Angaben vorliegen, die Größe des dritten Winkels dagegen stets zwangsläufig aus der Größe der beiden anderen resultiert. Ohne eine gegebene Seite ist zwar die Form des gesuchten Dreiecks gegeben, seine Größe aber bleibt unbestimmt.
Sinussatz und Kosinussatz
Die wichtigsten Werkzeuge für die Berechnung eines beliebigen Dreiecks sind neben der Winkelsumme im Dreieck der Sinus- und der Kosinussatz, denen gegenüber die weiteren Dreieckssätze wie der Projektionssatz und Tangentensatz sowie die Halbwinkelsätze nur eine untergeordnete Rolle spielen.
Das rechenaufwändigste, aber auch leistungsfähigste der drei Werkzeuge ist dabei der Kosinussatz, da man mit ihm als einzigem für ein Dreieck ohne alle Winkelangaben einen ersten Winkel berechnen (und sich anschließend mit dem einfacheren Sinussatz sowie der Winkelsumme im Dreieck weiterhelfen) kann. Dementsprechend verwendet man den Kosinussatz im hier diskutierten Zusammenhang nur zu Beginn der Berechnung eines Dreiecks vom Typ SSS oder SWS, während alles übrige einfacher und schneller per Sinussatz und Winkelsumme erledigt wird.
Wie nachfolgend zu sehen, beginnt der Kosinussatz genauso wie der Satz des Pythagoras, und in der Tat kann man diesen als einen Sonderfall des Kosinussatzes auffassen:
Wird nämlich der von zwei gegebenen Seiten eines Dreiecks eingeschlossene Winkel ein rechter, wird damit sein Kosinus gleich Null, und was dann von dem betreffenden Kosinussatz übrigbleibt, ist nichts anderes als eine weitere Version des „Pythagoras“.
Kennt man von einem Dreieck nur seine drei Seiten ,
und
,
lassen sich seine Innenwinkel unter Zuhilfenahme der Arkuskosinusfunktion
(arccos) wie folgt bestimmen:
Den Sinussatz gibt es in drei Varianten, die sich wie folgt zusammenfassen lassen:
Wie zu sehen, ist der Sinussatz rechnerisch wesentlich unkomplizierter: Kennt man einen der drei Brüche, kennt man damit automatisch auch alle übrigen. Dafür allerdings muss hier stets wenigstens einer der drei Innenwinkel schon bekannt sein, und, wenn nicht, zunächst einmal auf den Kosinussatz zurückgegriffen werden (s.o.).
Formeln
| Mathematische Formeln zum allgemeinen Dreieck | ||
|---|---|---|
| Flächeninhalt
(siehe Satz des Heron) |
| |
| Umfang | ||
| Höhe
aus den Seitenlängen (mittels Satz des Heron) |
||
| Höhe | ||
| Inkreisradius | ||
| Umkreisradius | ||
| Länge der Winkelhalbierenden | ||
| Länge der Seitenhalbierenden | ||
| Inkreismittelpunkt |
||
| Umkreismittelpunkt (baryzentrische Koordinaten) |
||
| Höhenschnittpunkt (baryzentrische Koordinaten) |
||
| Geometrischer
Schwerpunkt |
| |
Spezielle Dreiecke
Gleichseitige Dreiecke
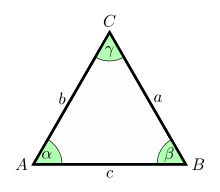
Eigenschaften
Ein Dreieck, bei dem alle drei Seiten gleich lang sind, wird gleichseitiges Dreieck genannt. Alle drei Innenwinkel sind gleich groß und betragen folglich 60° (es ist folglich ein spitzwinkliges Dreieck). Damit gehören die gleichseitigen Dreiecke zu den regelmäßigen Polygonen.
Alle gleichseitigen Dreiecke sind zueinander ähnlich und genau dann kongruent, wenn ihre Seitenlängen gleich sind. Mittelsenkrechte, Seitenhalbierende und Höhe zu einer Seite sowie Winkelhalbierende des gegenüberliegenden Winkels fallen bei einem gleichseitigen Dreieck jeweils aufeinander. Entsprechendes gilt für den Umkreismittelpunkt, den Inkreismittelpunkt, den Schwerpunkt und den Höhenschnittpunkt des gleichseitigen Dreiecks, sodass dieser Punkt häufig einfach Mittelpunkt genannt wird.
Formeln
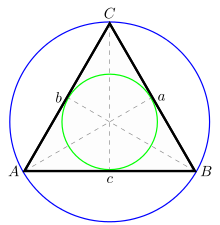
Für ein gleichseitiges Dreieck mit der Seitenlänge
gilt:
| Flächeninhalt | |
| Umfang | |
| Höhe | |
| Inkreisradius | |
| Umkreisradius |
Gleichschenklige Dreiecke
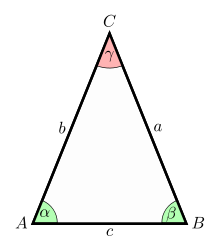
Ein gleichschenkliges Dreieck ist nach moderner Auffassung ein Dreieck, bei dem mindestens zwei Seiten gleich lang sind. Diese Seiten werden als Schenkel bezeichnet, die dritte Seite heißt Basis des gleichschenkligen Dreiecks. Die beiden Winkel an der Basis (Basiswinkel) sind gleich groß. Der Punkt, an dem beide Schenkel zusammentreffen, wird Spitze genannt, der dortige Winkel ist der Winkel an der Spitze.
Bei einem Geodreieck handelt es sich um ein Lineal in Form eines rechtwinkligen gleichschenkligen Dreiecks.
In einem gleichschenkligen Dreieck fallen die Mittelsenkrechte der
Basis, die Seitenhalbierende
der Basis und die Höhe auf der Basis sowie die
Winkelhalbierende
des Spitzenwinkels aufeinander. Man kann die Länge
dieser Strecke, also insbesondere die Höhe ,
bestimmen, indem man den Satz
des Pythagoras auf eine Hälfte des Dreiecks anwendet. Es ergibt sich
.
Rechtwinklige Dreiecke
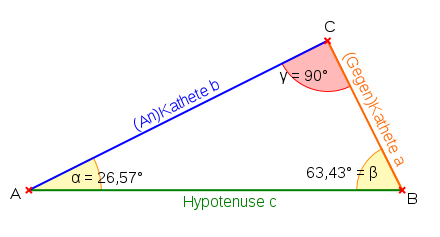
Ein rechtwinkliges Dreieck ist ein Dreieck, das einen 90°-Winkel, also einen rechten Winkel besitzt. Die dem rechten Winkel gegenüberliegende Seite ist die längste Seite des Dreiecks und wird Hypotenuse genannt. Die beiden anderen Seiten heißen Katheten. In Bezug auf einen der spitzen Winkel des Dreiecks bezeichnet man die dem Winkel anliegende Kathete als Ankathete und die dem Winkel gegenüberliegende Kathete als Gegenkathete.
Die Längen
der drei Seiten eines rechtwinkligen Dreiecks werden durch den Satz des Pythagoras
in Beziehung gebracht: Das Quadrat
der Länge der Hypotenuse
(in der Grafik als
bezeichnet) ist gleich der Summe der Quadrate der Längen der Katheten
(
und
).
Umgekehrt ist ein Dreieck, bei dem die Seitenlängen in der Beziehung
zueinander stehen, ein rechtwinkliges Dreieck mit Hypotenuse
.
Die Höhe
eines rechtwinkligen Dreiecks teilt die Hypotenuse
in zwei Teile
und
,
sodass die beiden Teildreiecke mit den Seiten
,
,
und
,
,
wiederum rechtwinklig sind. Bei Kenntnis zweier der sechs Angaben (
,
,
,
,
und
)
lassen sich die fehlenden vier anderen Werte aus den in folgender Tabelle
aufgeführten Formeln berechnen.
| Satz des Pythagoras | 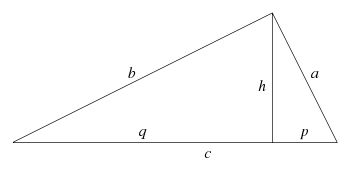 | |
| Kathetensatz von Euklid | ||
| Höhensatz von Euklid |
Winkelfunktionen im rechtwinkligen Dreieck
Durch das Verhältnis zwischen Katheten und Hypotenuse lassen sich auch die beiden spitzen Winkel des rechtwinkligen Dreiecks eindeutig bestimmen. Die folgenden sechs Funktionen werden Winkelfunktionen oder trigonometrische Funktionen genannt.
| Funktion | Berechnung |
|---|---|
| Der Sinus
des Winkels |
|
| Der Kosinus
des Winkels |
|
| Der Tangens ist durch das Verhältnis zwischen Gegenkathete und Ankathete gegeben. |
Aus den obigen können die folgenden durch Kehrwertbildung dargestellt werden.
| Funktion | Berechnung |
|---|---|
| Der Kotangens ist das Verhältnis zwischen Ankathete und Gegenkathete, also der Kehrwert des Tangens. | |
| Der Sekans ist das Verhältnis der Hypotenuse zur Ankathete, also der Kehrwert des Kosinus. | |
| Der Kosekans ist das Verhältnis der Hypotenuse zur Gegenkathete, also der Kehrwert des Sinus. |
Die Umkehrfunktionen der genannten Winkelfunktionen werden Arkussinus, Arkuskosinus, Arkustangens usw. genannt – ihre Hauptanwendung ist es dementsprechend, zu gegebenen Sinus-, Kosinus- oder Tangenswerten die dazugehörigen Winkel zu liefern.
Unregelmäßige Dreiecke
Unregelmäßig nennt man ein Dreieck, das diese zwei Bedingungen erfüllt:
- Alle drei Seiten sind unterschiedlich lang.
- Alle drei Winkel sind unterschiedlich groß.
Wenn eine der beiden Bedingungen erfüllt ist, ist die andere automatisch erfüllt.
Dreiecke der nichteuklidischen Geometrie
Sphärische Dreiecke
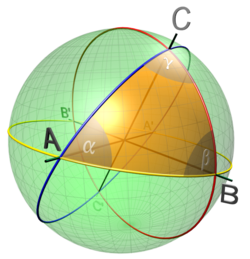
Dreiecke auf einer Kugel, deren drei Seiten Teile von Großkreisen sind, nennt man sphärische Dreiecke oder Kugeldreiecke. Ihre Seitenlängen werden nicht in der Dimension einer Länge angegeben (Meter, Zentimeter o.ä.), sondern als zugehöriger Winkel im Kugelmittelpunkt.
Ein sphärisches
Dreieck hat eine Winkelsumme
größer als 180°. Der „Überschuss“ wird sphärischer
Exzess genannt und in Formeln meist mit
bezeichnet:
.
Der maximale Exzess von 360° tritt bei einem „Dreieck“ mit drei auf 180°
gestreckten Winkeln auf. Dieses zum Großkreis
entartete Dreieck hat die Winkelsumme
3 · 180° = 540° und .
Der Exzess hängt direkt mit dem Flächeninhalt
des Dreiecks zusammen:
, bzw. in Grad
,
wobei
den Kugelradius
und
die Kreiszahl bedeutet.
Sphärische Dreiecke können analog den ebenen Dreiecken berechnet werden, wofür es in der Geodäsie z.B. den sphärischen Sinussatz, den Kosinussatz, den Projektionssatz und verschiedene Halbwinkelsätze gibt – siehe Sphärische Trigonometrie.
Hyperbolische Dreiecke
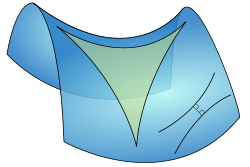
Zur nichteuklidischen Geometrie – in der das Parallelenaxiom nicht gilt – zählen auch Dreiecke auf einer Sattelfläche. Während eine Kugel überall konvex gekrümmt ist, haben Sattel- und andere hyperbolische Flächen sowohl konvexe als auch konkave Krümmung (ihr Produkt, das Krümmungsmaß, ist negativ).
Entsprechend ist auch der Exzess negativ – d.h. die Winkelsumme eines Dreiecks auf einer Sattelfläche ist kleiner als 180°. Die Kongruenzsätze machen Aussagen über die Dreiecksgrößen (Seitenlänge, Winkel), die notwendig sind, um ein Dreieck eindeutig zu bestimmen.
Sätze rund um das Dreieck
- Ähnlichkeitssätze
- Kongruenzsätze
- Satz des Pythagoras
- Satz des Heron
- Satz des Thales
- Satz von Stewart
- Kreise am Dreieck: Umkreis, Inkreis, Ankreise, Feuerbachkreis
- Eulersche Gerade
- Formelsammlung Trigonometrie
Dreieck als Symbol
Das Dreieck wird als Symbol verwendet, zum Beispiel in der Theologie, als ideologisches Symbol, als mathematisches Symbol und auch in Schildern.
Siehe auch
- Dreieckiges Prisma – wird durch die Parallelverschiebung eines Dreiecks entlang einer Gerade (die nicht in seiner Ebene liegt) aufgespannt
- Triangulation, Trilateration – Verfahren zur Positionsbestimmung
- Baryzentrische Koordinaten: Baryzentrische Koordinaten in der Dreiecksgeometrie
Literatur
- Max Koecher, Aloys Krieg: Ebene Geometrie. 3. Auflage. Springer, Berlin 2007, ISBN 978-3-540-49327-3.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 20.04. 2022