Steiner-Ellipse

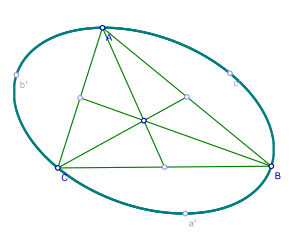
Die Steiner-Ellipse eines Dreiecks. Im Zentrum der Schwerpunkt des Dreiecks, der mit dem Mittelpunkt der Steiner-Ellipse übereinstimmt.

In der Geometrie ist die Steiner-Ellipse eines Dreiecks (zur Unterscheidung von der Steiner-Inellipse auch Steiner-Umellipse genannt) die eindeutig bestimmte Ellipse, die durch die Ecken des Dreiecks geht und deren Mittelpunkt der Schwerpunkt des Dreiecks ist. Die nach Jakob Steiner benannte Ellipse ist ein Beispiel für einen umbeschriebenen Kegelschnitt. Zum Vergleich: Auch der Umkreis eines Dreiecks ist ein solcher Kegelschnitt, der durch die Ecken verläuft; aber der Umkreismittelpunkt fällt nicht mit dem Schwerpunkt zusammen – außer wenn das Dreieck gleichseitig ist.

Der Flächeninhalt der Steiner-Ellipse ist gleich dem ${\tfrac {4\pi }{3{\sqrt {3}}}}$ -fachen Flächeninhalt des Dreiecks und folglich viermal so groß wie der Inhalt der Steiner-Inellipse. Die Steiner-Ellipse hat den kleinsten Flächeninhalt unter allen dem Dreieck umbeschriebenen Ellipsen.

Eigenschaft einer Steiner-Ellipse

Steiner-Ellipse eines gleichseitigen (links) und gleichschenkligen Dreiecks

Eine Steiner-Ellipse ist die einzige Ellipse, die den Schwerpunkt eines Dreiecks als Mittelpunkt besitzt und durch die Ecken des Dreiecks verläuft. Der Flächeninhalt der Steiner-Ellipse ist gleich dem ${\tfrac {4\pi }{3{\sqrt {3}}}}$ -fachen Flächeninhalt des Dreiecks.

Beweis

A) Bei einem gleichseitigen Dreieck ist die Ellipse offensichtlich der Umkreis. Er ist die einzige Ellipse, die die Forderungen erfüllt. Denn da der Mittelpunkt der Ellipse ist, müssen auch die drei an gespiegelten Ecken auf der Ellipse liegen. Dies ist für den Umkreis der Fall. Da ein Kegelschnitt durch 5 Punkte eindeutig bestimmt ist, ist der Kreis die einzige Ellipse mit der geforderten Eigenschaft.

B) Da ein beliebiges Dreieck als affines Bild eines gleichseitigen Dreiecks angesehen werden kann, ein Kreis bei einer affinen Abbildung in eine Ellipse und der Schwerpunkt eines Dreiecks in den Schwerpunkt des Bilddreiecks übergeht, gilt die Eigenschaft (genau eine Umellipse mit Mittelpunkt im Schwerpunkt) für alle Dreiecke.

Die Fläche des Umkreises eines gleichseitigen Dreiecks ist gleich dem ${\tfrac {4\pi }{3{\sqrt {3}}}}$ -fachen Flächeninhalt des Dreiecks. Bei einer affinen Abbildung bleiben Flächenverhältnisse unverändert. Also gilt diese Aussage über das Flächenverhältnis auch bei einem beliebigen Dreieck und seiner Steiner-Ellipse.

Konstruktion von konjugierten Halbmessern

Um eine Ellipse zeichnen zu können, benötigt man wenigstens zwei konjugierte Halbmesser. Dann lassen sich

entweder mit Hilfe einer Rytz-Konstruktion die Scheitel bestimmen und mit einem Ellipsenzirkel die Ellipse zeichnen
oder mit einem Computerprogramm die Ellipse als parametrisierte Kurve zeichnen.

Die Scheitel und Halbachsen und daher auch die Exzentrizität lassen sich auch rechnerisch bestimmen.

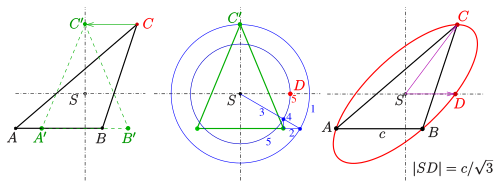
Bild 1: Konstruktionsschritte einer zeichnerischen Bestimmung der Steiner-Ellipse
1) Scherung des Dreiecks zu einem gleichschenkligen
2) Bestimmung des Punktes (Schritte 1–5)
3) Zeichnen der Ellipse mit Hilfe der konjugierten Halbmesser $SC,SD$

Zeichnerische Bestimmung der Steiner-Ellipse

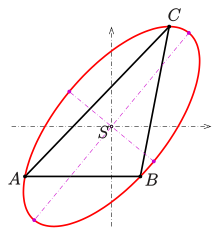
Es sei ABC ein Dreieck (Bild 1) und dessen Schwerpunkt. Legt man durch eine Parallele zur Seite und führt das Dreieck durch eine Scherung an in ein gleichschenkliges Dreieck A'B'C' über (s. Bild), so ist ein Scheitel der Steiner-Ellipse des Dreiecks A'B'C' . Ein weiterer Scheitel dieser Ellipse liegt auf , da zu $SC'$ (aus Symmetriegründen) senkrecht ist. Dieser Scheitel lässt sich aus den Daten (Ellipse mit Mittelpunkt durch und , $|A'B'|=c$ ) berechnen. Es ergibt sich:

$|SD|={\frac {c}{\sqrt {3}}}$

Oder: Man bestimmt zeichnerisch mit Hilfe der Ellipsen-Konstruktion von de la Hire (s. mittleres Bild) den Scheitel der Umellipse des gleichschenkligen Dreiecks A'B'C' .
Macht man die Scherung rückgängig, geht wieder in über und bleibt als Punkt der Scherachse fest. Damit ist ein zu $SC$ konjugierter Halbmesser. I.A. stehen beide nicht senkrecht aufeinander.
Mit Hilfe dieser konjugierten Halbmesser lässt sich, wie oben beschrieben, die gesuchte Steiner-Ellipse zeichnen.

Alternative Konstruktion des zweiten Halbmessers

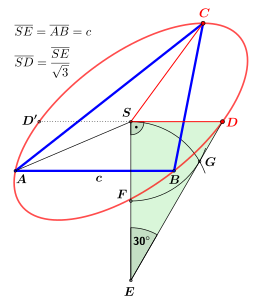
Bild 2: Steiner-Ellipse, alternative Konstruktion des Halbmessers ${\overline {SD}}$ mit Hilfe des rechtwinkligen Dreiecks $SED$

Gegeben sei das Dreieck ABC (Bild 2) und dessen Schwerpunkt

Zuerst erfolgt die Berechnung des Halbmessers ${\overline {SD}}.$ Als Ansatz dient die allgemeine Formel für die Höhe des gleichseitigen Dreiecks mit der Seite

$h={\frac {\sqrt {3}}{2}}\cdot a$

Die Hälfte dieses gleichseitigen Dreiecks ist ein rechtwinkliges Dreieck mit der (gleichen) Höhe:

$h={\frac {\sqrt {3}}{2}}\cdot 2\cdot {\frac {a}{2}}={\sqrt {3}}\cdot {\frac {a}{2}}$

Setzt man ${\overline {AB}}=c={\overline {SE}},$ ${\overline {ED}}=a,$ ${\frac {a}{2}}={\overline {SD}}$ und $h=c$ ein, ergibt dies das rechtwinklige Dreieck $SED$ mit der Höhe

$c={\sqrt {3}}\cdot {\overline {SD}},$

umgeformt gilt

${\overline {SD}}={\frac {c}{\sqrt {3}}}.$

Es geht weiter mit der Konstruktion des rechtwinkligen Dreiecks $SED:$

Sie beginnt mit dem Einzeichnen einer Senkrechten (Orthogonalen) zu ${\overline {AB}},$ ab dem Schwerpunkt und dem Übertragen der Strecke ${\overline {AB}}=c$ auf die Senkrechte; es ergibt die Strecke ${\overline {SE}}.$ Nun folgt die Konstruktion der Winkelweite $30^{\circ }$ am Winkelscheitel indem man die Strecke ${\overline {SE}}$ in halbiert, einen Kreisbogen mit Radius ${\overline {FS}}$ um den Punkt und einen weiteren Kreisbogen mit derselben Zirkelöffnung um den Punkt zieht; dabei ergibt sich der Schnittpunkt Durch das Einzeichnen einer Halbgeraden, ab durch , wird am Winkelscheitel der Winkel $30^{\circ }$ generiert. Die abschließende Parallele zur Strecke ${\overline {AB}},$ > ab dem Schwerpunkt erzeugt den Schnittpunkt auf der Halbgeraden und liefert somit den zu ${\overline {SC}}$ konjugierten Halbmesser ${\overline {SD}}.$

Die fünf Ellipsen-Punkte $D,C,D',A$ und ermöglichen das exakte Einzeichnen der Ellipsenlinie, z.B. mit Hilfe einer Dynamischen-Geometrie-Software (DGS).

Parameterdarstellung und Gleichung

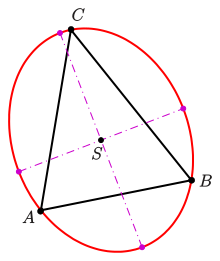
Steiner-Ellipse eines Dreiecks mit Achsen und Scheiteln (magenta)

Gegeben: Dreieck $\ A=(a_{1},a_{2}),\;B=(b_{1},b_{2}),\;C=(c_{1},c_{2})$
Gesucht: Parameterdarstellung und Gleichung der zugehörigen Steiner-Ellipse.

Der Schwerpunkt des Dreiecks ist $\ S=({\tfrac {a_{1}+b_{1}+c_{1}}{3}},{\tfrac {a_{2}+b_{2}+c_{2}}{3}})\ .$

Parameterdarstellung:

Aus den Überlegungen des vorigen Abschnitts ergibt sich die folgende Parameterdarstellung der Steiner-Ellipse:

${\vec {x}}={\vec {p}}(t)={\overrightarrow {OS}}\;+\;{\overrightarrow {SC}}\;\cos t\;+\;{\frac {1}{\sqrt {3}}}{\overrightarrow {AB}}\;\sin t\;,\quad 0\leq t<2\pi$

Die 4 Scheitel der Ellipse sind

${\vec {p}}(t_{0}),\;{\vec {p}}(t_{0}\pm {\frac {\pi }{2}}),\;{\vec {p}}(t_{0}+\pi ),$

wobei sich $t_{0}$ aus

$\cot(2t_{0})={\tfrac {{\vec {f}}_{1}^{\,2}-{\vec {f}}_{2}^{\,2}}{2{\vec {f}}_{1}\cdot {\vec {f}}_{2}}}\quad$ mit $\quad {\vec {f}}_{1}={\vec {SC}},\quad {\vec {f}}_{2}={\frac {1}{\sqrt {3}}}{\vec {AB}}$

ergibt (s. Ellipse).

Die Rollen der Punkte bei der Aufstellung der Parameterdarstellung können beliebig vertauscht werden.

Beispiel (s. Bild): $A=(-5,-5),B=(0,25),C=(20,0)$

Steiner-Ellipse als Beispiel zu „Gleichung“

Gleichung:

Falls der Nullpunkt der Schwerpunkt ist, ist die Gleichung der Ellipse mit der Parameterdarstellung ${\vec {x}}={\vec {f}}_{1}\cos t+{\vec {f}}_{2}\sin t$

$(xf_{2y}-yf_{2x})^{2}+(yf_{1x}-xf_{1y})^{2}-(f_{1x}f_{2y}-f_{1y}f_{2x})^{2}=0$

mit

${\vec {f}}_{i}=(f_{ix},f_{iy})^{T}$ .

Beispiel: Für das Dreieck $\quad A=(-{\tfrac {3}{2}}{\sqrt {3}},-{\tfrac {3}{2}}),\ B=({\tfrac {\sqrt {3}}{2}},-{\tfrac {3}{2}}),\ C=({\sqrt {3}},3)\quad$ liegt der Schwerpunkt im Nullpunkt und es ist

${\vec {f}}_{1}=({\sqrt {3}},3)^{T},\ {\vec {f}}_{2}=(2,0)^{T}$ .

Die Gleichung der Steiner-Ellipse ist:

$9x^{2}+7y^{2}-6{\sqrt {3}}xy-36=0$

Berechnung der Halbachsen

Hat man die Scheitel der Steiner-Ellipse schon bestimmt (s. vorigen Abschnitt), lassen sich daraus die Halbachsen berechnen. Ist man überhaupt nur an den Halbachsen interessiert, so führt die folgende Methode schneller zum Ziel:

Sind $a,b,\;a>b$ die Halbachsen der Steiner-Ellipse, so folgt aus den Sätzen des Apollonios über Eigenschaften konjugierter Halbmesser von Ellipsen:

$a^{2}+b^{2}={\vec {SC}}^{2}+{\vec {SD}}^{2}\ ,\quad a\cdot b=\left|\det({\vec {SC}},{\vec {SD}})\right|$

Bezeichnet man die jeweils rechte Seite mit bzw. , formt das nichtlineare Gleichungssystem (unter Berücksichtigung von $a>b>0$ ) um zu

$a^{2}+b^{2}=M,\ ab=N\quad \rightarrow \quad a^{2}+2ab+b^{2}=M+2N,\ a^{2}-2ab+b^{2}=M-2N$

$\rightarrow \quad (a+b)^{2}=M+2N,\ (a-b)^{2}=M-2N\quad \rightarrow \quad a+b={\sqrt {M+2N}},\ a-b={\sqrt {M-2N}}$

und löst nach und auf, so erhält man für die Halbachsen:

$a={\frac {1}{2}}({\sqrt {M+2N}}+{\sqrt {M-2N}})$

$b={\frac {1}{2}}({\sqrt {M+2N}}-{\sqrt {M-2N}})$

Außerdem gilt:

$M={\vec {SC}}^{2}+{\frac {1}{3}}{\vec {AB}}^{2}$

$N={\frac {1}{\sqrt {3}}}\left|\det({\vec {SC}},{\vec {AB}})\right|$

Für die lineare Exzentrizität der Steiner-Ellipse ergibt sich:

$e={\sqrt {a^{2}-b^{2}}}=\dotsb ={\sqrt {\sqrt {M^{2}-4N^{2}}}}$

Der Flächeninhalt ist:

$F=\pi ab=\pi N={\frac {\pi }{\sqrt {3}}}\left|\det({\vec {SC}},{\vec {AB}})\right|$

Trilineare und baryzentrische Gleichung

Die Gleichung der Steiner-Umellipse in trilinearen Koordinaten ist

$vwyz+wuzx+uvxy=0$ ,

wobei $u,v,w$ die Seitenlängen des Dreiecks bezeichnen.

Eine besonders einfache Gleichung erhält man, wenn man baryzentrische Koordinaten verwendet:

$yz+zx+xy=0$

Alternative Berechnung der Halbachsen und Brennpunkte

Die Längen der großen und kleinen Halbachse für ein Dreieck mit Seitenlängen $u,v,w$ sind

${\frac {1}{3}}{\sqrt {u^{2}+v^{2}+w^{2}\pm 2Z}}$

mit der Abkürzung

$Z:={\sqrt {u^{4}+v^{4}+w^{4}-u^{2}v^{2}-v^{2}w^{2}-w^{2}u^{2}}}.$

Die lineare Exzentrizität ist

${\frac {2}{3}}{\sqrt {Z}}$ .

Die Brennpunkte der Steiner-Ellipse sind die sogenannten Bickart-Punkte des Dreiecks.

Basierend auf einem Artikel in:

Wikipedia.de