Kugeldreieck

Kugeldreieck

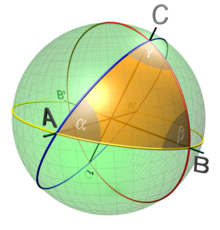
Ein Kugeldreieck oder sphärisches Dreieck ist in der sphärischen Geometrie (Kugelgeometrie) ein Teil einer Kugeloberfläche, der von drei Großkreisbögen begrenzt wird. Als Ecken des Kugeldreiecks werden die Punkte bezeichnet, in denen je zwei dieser Großkreise einander schneiden.

Ähnlich wie bei Dreiecken in der ebenen Geometrie spricht man von den Seiten und Winkeln eines Dreiecks. Allerdings versteht man unter der Länge einer Seite nicht die Länge des Kreisbogens, sondern den zugehörigen Mittelpunktswinkel (Zentriwinkel). Im Bogenmaß ist der Wert dieses Winkels genau die Länge des Kreisbogens geteilt durch den Radius der Kugel:

$\text{Winkel} = \frac{\text{Kreisbogen}}{\text{Radius}}$

Zur Definition von Längen auf einer Kugel wählt man also die Skala zunächst so, dass die Kugel eine Einheitskugel ist, und nimmt dann in dieser Skala erst die Länge des Kreisbogens. Eine Seite, die also beispielsweise einem Viertel des Kugel- und Großkreisumfangs entspricht, hat die Länge ${\tfrac {\pi }{2}}$ (also 90°). Die Innenwinkel (an den drei Ecken) sind definiert durch die Tangenten der Seiten – also die Schnittwinkel zwischen den Ebenen, in denen die begrenzenden Großkreisbögen liegen.

Eulersche Kugeldreiecke

Meist schränkt man den Begriff des Kugeldreiecks ein auf eulersche Kugeldreiecke (benannt nach Leonhard Euler), d.h. auf Kugeldreiecke, in denen alle Winkel kleiner als $\pi$ bzw. 180° und daraus folgend alle Seiten kleiner als $r \cdot \pi$ (auf der Einheitskugel: $\pi$ ) sind. Ohne diese Einschränkung gäbe es zu drei beliebigen Punkten der Kugeloberfläche, die nicht alle auf einem gemeinsamen Großkreis liegen, mehrere Kugeldreiecke. Anschaulich kann man dies mit der Forderung nach dem kürzesten Bogenstück des Kreises machen, wenn man sich vorstellt, dass zwei Punkte auf einem Kreis genau dann am weitesten voneinander entfernt sind, wenn sie sich (diametral) gegenüberliegen, d.h. also 180° voneinander entfernt sind. Kommt man über die 180° hinaus, ist das Bogenstück zwar in der einen Richtung größer, aber in der anderen Richtung kleiner als 180°, weshalb letzteres wieder als Seite eines eulerschen Dreiecks aufgefasst werden kann.

Eigenschaften sphärischer Dreiecke

Flächeninhalt

Der Flächeninhalt A_D eines Kugeldreiecks lässt sich aus den Winkeln $\alpha, \beta$ und $\gamma$ des Dreiecks (im Bogenmaß) und dem Kugelradius berechnen:

$A_D = (\alpha + \beta + \gamma - \pi) \cdot r^2.$

Dieser Zusammenhang leitet sich folgendermaßen her:

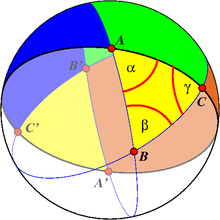
Zur Flächenberechnung am Kugeldreieck

Die drei durch die Eckpunkte eines Dreiecks ABC bestimmten Großkreise unterteilen die Kugeloberfläche in acht Dreiecke bzw. vier Gegendreieckspaare. Das in der Abbildung grün eingefärbte Dreieck bildet mit dem gelb eingefärbten Dreieck ABC ein Zweieck mit dem Öffnungswinkel $\beta$ . Die blau und rot eingefärbten Dreiecke bilden mit dem Gegendreieck A’B’C’ Zweiecke mit den Öffnungswinkeln $\alpha$ bzw. $\gamma$ .

Für die Flächeninhalte der Zweiecke gilt:

$(I) \quad A_\alpha = 2\alpha \cdot r^2$

(Analog für die Zweiecke mit den Öffnungswinkeln $\beta$ und $\gamma$ .)

Für die Flächeninhalte A_b des blauen, A_g des grünen und A_r des roten Dreiecks gilt:

$A_b = A_\alpha - A_D$

$A_g = A_\beta - A_D$

$A_r = A_\gamma - A_D$

Zusammen mit dem gelben Gegendreieck A’B’C’ füllen das blaue, das grüne und das rote Dreieck die Hälfte der Kugeloberfläche aus:

$\frac{A_K}{2} = A_b + A_g + A_r + A_D$

Setzt man (I) ein, ergibt sich:

$\frac{A_K}{2} = (A_\alpha - A_D) + (A_\beta - A_D) + (A_\gamma - A_D) + A_D$

$= A_\alpha + A_\beta + A_\gamma - 2A_D$

Mit den Gleichungen zur Berechnung der Kugeloberfläche und der Kugelzweiecke erhält man:

$\frac {4 \pi r^2}{2}= 2 \alpha r^2 + 2 \beta r^2 + 2 \gamma r^2 - 2 A_D$

Für A_D ergibt sich also:

$A_D = \alpha r^2 + \beta r^2 + \gamma r^2 - \pi r^2$

$= (\alpha + \beta + \gamma - \pi)\cdot r^2$

Innenwinkelsumme und sphärischer Exzess

Auf der Einheitskugel mit dem Radius 1 gilt nach obiger Betrachtung für den Flächeninhalt:

$A_D=\alpha + \beta + \gamma - \pi$

Die Summe $\alpha + \beta + \gamma - \pi$ wird als sphärischer Exzess (von lat. excedere „überschreiten“) bezeichnet, und gibt an, um wie viel die Innenwinkelsumme den Wert $\pi$ ( $=180^\circ$ ) übersteigt. Im Gegensatz zum euklidischen Dreieck ist die Innenwinkelsumme im Kugeldreieck nicht konstant $\pi$ . Für sie gilt (als Konsequenz der Formel für den Flächeninhalt) im allgemeinen Kugeldreieck:

$\pi < \alpha + \beta + \gamma < 5\pi$

im eulerschen Kugeldreieck:

$\pi < \alpha + \beta + \gamma < 3\pi$

Bei einem kleinen Kugeldreieck („klein“ im Vergleich zur gesamten Kugeloberfläche) übersteigt die Innenwinkelsumme $\pi$ nur wenig, da sich das Dreieck dem ebenen Fall des Innen-Winkelsummensatzes annähert (Verebnung). Der Satz von Legendre besagt, wie sphärische Dreiecke geringer Größe durch Reduktion der Winkel verebnet werden können. Überdeckt das Dreieck hingegen fast die halbe Kugeloberfläche (3 Winkel zu fast $\pi$ ), so ist die Winkelsumme nur wenig kleiner als $3\pi$ und der Exzess daher beinahe $2\pi$ .

Seitensumme (auf der Einheitskugel)

Im allgemeinen sphärischen Dreieck gilt für die Seitensumme:

$0 < a + b + c < 6 \pi$

Im eulerschen Kugeldreieck gilt für die Seitensumme:

$0 < a + b + c < 2 \pi$

Im Allgemeinen ist durch sww ein Dreieck nicht eindeutig bestimmt.

Kongruenzsätze

Die Seiten a, b und c bestimmen zwei komplementäre Dreiecke (blau und grün eingefärbt).

Zu den gegebenen Größen a, b und γ gibt es zwei dritte Seiten.

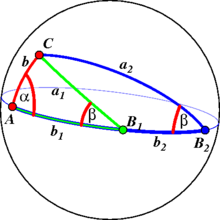
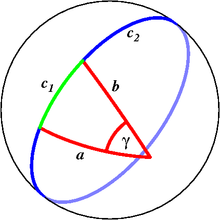
Auf der Kugel muss man zwischen den Kongruenzsätzen zu eulerschen und nichteulerschen Dreiecken unterscheiden. Für beide gilt, dass ähnliche Dreiecke bereits kongruent sind (ihr Flächeninhalt ist aufgrund der Proportionalität zum sphärischen Exzess bereits gleich). Der im euklidischen Dreieck gültige Kongruenzsatz sww (Seite-Winkel-Winkel) hat auf der Kugel hingegen keine Gültigkeit (vgl. Abbildung). Die Kongruenzverhältnisse in eulerschen Dreiecken sind der folgenden Tabelle zu entnehmen.

Übersicht zu den Kongruenzsätzen in eulerschen Dreiecken (zur Dualisierung vgl. entsprechenden Abschnitt im Artikel Sphärische Geometrie)

gegebene Dreiecksstücke	dual dazu	Kongruenzklasse eindeutig bestimmt?
sss	www	ja
ssw	sww	nein
sws	wsw	ja

In nichteulerschen Dreiecken bestimmen sss und sws noch keine eindeutige Kongruenzklasse (vgl. Abbildungen).

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de