Logistische Funktion

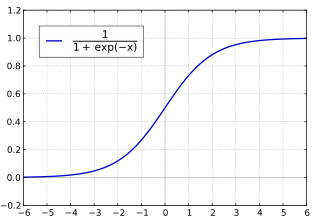
Logistische Funktion für den Fall $G=1\,;\,k=1\,;\,f(0)=0{,}5$

Die logistische Funktion charakterisiert eine stetige eindimensionale Wahrscheinlichkeitsverteilung (die logistische Verteilung) und ist eine funktionelle Darstellung von Sättigungsprozessen aus der Klasse der sogenannten Sigmoidfunktionen mit unbegrenzter zeitlicher Ausdehnung.

Der Graph der Funktion beschreibt eine S-förmige Kurve, ein Sigmoid. Heute ist der Name logistische Kurve eindeutig der S-Funktion zugeordnet, wohingegen noch bis ins 20. Jahrhundert gelegentlich auch der Logarithmus mit dem italienischen Namen der logistischen Kurve (curva logistica) belegt wurde.

Die Funktion wird manchmal auch mit Expit bezeichnet, da die Umkehrfunktion der logistischen Funktion die Logit-Funktion ist.

Beschreibung

Die logistische Funktion, wie sie sich aus der diskreten logistischen Gleichung ergibt, beschreibt den Zusammenhang zwischen der verstreichenden Zeit und einem Wachstum. Hierzu wird das Modell des exponentiellen Wachstums modifiziert durch eine sich mit dem Wachstum verbrauchende Ressource, die eine obere Schranke darstellt.

Zur Anfangszeit ist der Funktionswert nicht 0, sondern es gilt $f(0)>0$ .

Es gilt:

Die obere Schranke $G$ bildet eine Grenze für den Funktionswert $f(t)$ .
Das Wachstum ist proportional zu:
- dem aktuellen Bestand $f(t)$ ,
- der noch vorhandenen Kapazität $G-f(t)$
- und einer Wachstumskonstanten $k$ .

Diese Entwicklung wird daher durch eine Bernoullische Differentialgleichung der Form

$f'(t)=k\cdot f(t)\cdot \left(G-f(t)\right)$

mit einer Proportionalitätskonstanten $k$ beschrieben. Das Lösen dieser Differentialgleichung ergibt:

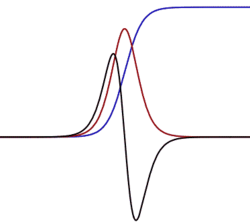
$f(t)=G\cdot {\frac {1}{1+\mathrm {e} ^{-k\cdot G\cdot t}\left({\frac {G}{f(0)}}-1\right)}}.$

Logistische Funktion (blau) mit erster (rot) und zweiter Ableitung (schwarz)

Am Anfang ist das Wachstum klein, da die Population und somit die Zahl der sich vermehrenden Individuen gering ist. In der Mitte der Entwicklung (genauer: im Wendepunkt) wächst die Population am stärksten, bis sie durch die sich erschöpfenden Ressourcen gebremst wird. Die erste Ableitung der logistischen Funktion ist vom Typ einer Glockenkurve, d. h. am Wendepunkt hat das Wachstum das Maximum (= höchste Steigung von f) und gegen unendlich (-∞; +∞) strebt der Wert gegen Null, was ähnlich einer Gaußschen Normalverteilung aussieht, aber sich im Detail unterscheidet, vgl. auch mit Logit und Probit-Transformation.

Die beiden stationären Lösungen der Differentialgleichung sind $f\equiv 0$ und $f\equiv G$ .

Anwendungen

>Beispiel einer Epidemie: Krankheits- und Todesfälle (schwarz) im Verlauf der Ebolafieber-Epidemie in Westafrika bis Juli 2014 (annähernd logistische Funktionen)

Die logistische Gleichung beschreibt einen sehr häufig auftretenden Zusammenhang, wie der Beschreibung einer Population von Lebewesen, beispielsweise einer idealen Bakterienpopulation, die auf einem Bakteriennährboden begrenzter Größe wächst. Ein weiteres Beispiel ist (annähernd) die Verbreitung einer Infektionskrankheit mit anschließender permanenter Immunität, bei der mit der Zeit eine abnehmende Anzahl für die Infektionskrankheit anfällige Individuen übrig bleiben.

Die Funktion findet weit über den Modellen aus der Biologie hinaus Anwendung. Auch der Lebenszyklus eines Produktes im Markt kann mit der logistischen Funktion nachgebildet werden. Weitere Anwendungsbereiche sind Wachstums- und Zerfallsprozesse in der Sprache.

Lösung der Differentialgleichung

Sei $F\colon \mathbb {R} \to \mathbb {R} ,t\mapsto kt(G-t)$ . $F$ ist stetig. Es gilt, die Differentialgleichung

${\frac {\mathrm {d} f}{\mathrm {d} t}}(t)=F(f(t))$

zu lösen.

Die Differentialgleichung lässt sich mit dem Verfahren „Trennung der Variablen“ lösen. Es gilt $F(t)\neq 0$ für alle $t\in \mathbb {R}$ , also ist die Abbildung

$\Phi (t):=\int _{0}^{t}{\frac {1}{F(s)}}\,{\mathrm {d} }s$

auf den reellen Zahlen wohldefiniert.

Nach der Trennung der Variablen ist die Lösung $f$ der obigen Differentialgleichung also identisch mit der Lösung der Differentialgleichung

$\int _{f(0)}^{f(t)}{\frac {1}{F(s)}}\,\mathrm {d} s=t.$

Durch Partialbruchzerlegung ergibt sich

$\int _{f(0)}^{f(t)}{\frac {1}{F(s)}}\,\mathrm {d} s=\int _{f(0)}^{f(t)}{\frac {1}{ks(G-s)}}\,\mathrm {d} s={\frac {1}{kG}}\int _{f(0)}^{f(t)}\left({\frac {1}{s}}+{\frac {1}{G-s}}\right)\,\mathrm {d} s.$

Nach dem Hauptsatz der Differential- und Integralrechnung ist das obige Integral

$=\left.{\frac {1}{kG}}{\bigg (}\ln(s)-\ln(G-s){\bigg )}\right|_{s=f(0)}^{s=f(t)}={\frac {1}{kG}}\left(\ln \left({\frac {f(t)}{G-f(t)}}\right)+c\right)$

wobei

$c:=-\ln {\frac {f(0)}{G-f(0)}}=\ln \left({\frac {G}{f(0)}}-1\right).$

Es gilt also, die Funktionsgleichung

$\ln {\frac {f(t)}{G-f(t)}}=kGt-c$

zu lösen, solange die $f(t)$ zwischen $0$ und $G$ liegen, was wegen der Voraussetzung $0<f(0)<G$ angenommen werden kann. Dabei ist $\ln$ der natürliche Logarithmus. Die Anwendung der Exponentialfunktion auf beiden Seiten führt zu

$\mathrm {e} ^{kGt-c}\,=\,{\frac {f(t)}{G-f(t)}}$

und anschließende Kehrwertbildung zu

$(*)\quad \quad \quad \mathrm {e} ^{-kGt+c}\,=\,{\frac {G-f(t)}{f(t)}}\,=\,{\frac {G}{f(t)}}-1.$

Wir bringen nun die $1$ auf die linke Seite, bilden dann erneut den Kehrwert, und erhalten schließlich

${\frac {f(t)}{G}}\,=\,{\frac {1}{1+\mathrm {e} ^{-kGt+c}}}$

und daraus

$(**)\quad \quad \quad f(t)\,=\,G\cdot {\frac {1}{1+\mathrm {e} ^{-kGt+c}}}.$

Setzen wir die Definition von $c$ in die gefundene Lösung (**) ein, so kommen wir zur oben behaupteten Lösung der logistischen Differentialgleichung:

$f(t)\,=\,G\cdot {\frac {1}{1+\mathrm {e} ^{-kGt+c}}}\,=\,G\cdot {\frac {1}{1+\mathrm {e} ^{-kGt}\mathrm {e} ^{c}}}\,=\,G\cdot {\frac {1}{1+\mathrm {e} ^{-kGt}\left({\frac {G}{f(0)}}-1\right)}}.$

An dieser Funktionsgleichung liest man leicht ab, dass die Werte immer zwischen $0$ und $G$ liegen, weshalb die Lösung für alle $-\infty <t<\infty$ gilt. Das kann man im Nachhinein natürlich auch durch Einsetzen in die Differentialgleichung bestätigen.

Berechnung des Wendepunkts

Zur Bestimmung des Wendepunktes der Lösungsfunktion $f$ bestimmen wir zunächst mittels Produktregel die Ableitungen

${\begin{aligned}f'(t)&=k\cdot f(t)\cdot (G-f(t))\\f''(t)&=k\cdot f'(t)\cdot (G-f(t))+k\cdot f(t)\cdot (-f'(t))\\&=k\cdot f'(t)\cdot (G-f(t)-f(t))=k\cdot f'(t)\cdot (G-2\cdot f(t))\end{aligned}}$

und bestimmen die Nullstelle $t_{\mathrm {W} }$ der zweiten Ableitung:

$f''(t_{\mathrm {W} })=k\cdot f'(t_{\mathrm {W} })\cdot (G-2\cdot f(t_{\mathrm {W} }))=0$

$G-2\cdot f(t_{\mathrm {W} })=0$

$G=2\cdot f(t_{\mathrm {W} })$

$f(t_{\mathrm {W} })={\tfrac {G}{2}}.$

Damit kennen wir den Funktionswert im Wendepunkt und stellen fest, dass die Population im Wendepunkt gerade die halbe Sättigungsgrenze überschreitet. Zur Bestimmung von $t_{\mathrm {W} }$ verwenden wir für $f(t_{\mathrm {W} })={\tfrac {G}{2}}$ die Lösungsformel und rechnen wie folgt:

$G\cdot {\frac {1}{1+\mathrm {e} ^{-k\cdot G\cdot t_{\mathrm {W} }}\cdot \mathrm {e} ^{c}}}={\frac {G}{2}}$

$1+\mathrm {e} ^{-k\cdot G\cdot t_{\mathrm {W} }}\cdot \mathrm {e} ^{c}=2$

$\mathrm {e} ^{-k\cdot G\cdot t_{\mathrm {W} }}\cdot \mathrm {e} ^{c}=1=\mathrm {e} ^{0}$

$-k\cdot G\cdot t_{\mathrm {W} }+c=0$

$t_{\mathrm {W} }={\frac {c}{k\cdot G}}.$

Für $\textstyle G>f(0)$ folgt mit $\textstyle \mathrm {e} ^{c}={\frac {G}{f(0)}}-1\Rightarrow c=\ln \left({\frac {G}{f(0)}}-1\right)$ weiter:

$t_{\mathrm {W} }={\frac {\ln \left({\frac {G}{f(0)}}-1\right)}{k\cdot G}}.$

Damit ist der Wendepunkt vollständig bestimmt und es gibt nur diesen einen. Durch Einsetzen von $f(t_{\mathrm {W} })={\tfrac {G}{2}}$ in die erste Ableitung erhält man die maximale Wachstumsgeschwindigkeit:

$f'(t_{\mathrm {W} })=k\cdot {\frac {G}{2}}\cdot \left(G-{\frac {G}{2}}\right)=k\cdot {\frac {G}{2}}\cdot {\frac {G}{2}}$

$f'(t_{\mathrm {W} })={\frac {k\cdot G^{2}}{4}}.$

Weitere Darstellungen

Aus

$f(t)=G\cdot {\frac {1}{1+\mathrm {e} ^{-k\cdot G\cdot t}\left({\frac {G}{f(0)}}-1\right)}}$

folgt:

$f(t)=G\cdot {\frac {1}{1+\mathrm {e} ^{-k\cdot G\cdot t}\cdot {\frac {G}{f(0)}}-\mathrm {e} ^{-k\cdot G\cdot t}}}\cdot {\frac {f(0)}{f(0)}}={\frac {G\cdot f(0)}{f(0)+\mathrm {e} ^{-k\cdot G\cdot t}\cdot G-\mathrm {e} ^{-k\cdot G\cdot t}\cdot f(0)}}$

$={\frac {G\cdot f(0)}{f(0)+\left(G-f(0)\right)\cdot \mathrm {e} ^{-k\cdot G\cdot t}}}$

oder auch:

$f(t)={\frac {G}{2}}\cdot \left(\tanh \left({\frac {kG}{2}}(t-t_{\mathrm {W} })\right)+1\right)$ ,

wobei $t_{\mathrm {W} }$ die oben berechnete Wendestelle ist:

$t_{\mathrm {W} }={\frac {\ln \left({\frac {G}{f(0)}}-1\right)}{k\cdot G}}.$

Umrechnung von stetigem exponentiellem in logistisches Wachstum

Oft werden Prognosen auf Basis von stetigem exponentiellem Wachstum angegeben (Wirtschaftswachstum, Infektionszahlen, Vermehrung). Diese Prognosen erweisen sich stets als unzutreffend, sobald der betrachtete Prozess in die Phase der Sättigung kommt. Spätestens dann ist es günstiger, das Modell „exponentielles Wachstum“ der Form $y(t)=A\cdot e^{\lambda \cdot t}$ durch das Modell „logistisches Wachstum“ zu ersetzen. Die Wachstumsfaktoren $k$ der logistischen Funktion und $\lambda$ der e-Funktion unterscheiden sich hier beträchtlich.

In allen Fällen werden zwei Punkte innerhalb der (vermeintlichen) exponentiellen Wachstumsphase benötigt. Hier wird davon ausgegangen, dass der erste Punkt bei $A=f(t=0)$ liegt.

Da der zweite Punkt $P(T/Y)$ in der exponentiellen Wachstumsphase liegt, gilt: $G\gg Y\Rightarrow {\frac {G}{Y}}\gg 1\Rightarrow {\frac {G}{Y}}-1\approx {\frac {G}{Y}}$ .

Damit gilt aus den ug. Formeln für $\lambda$ und $k$ näherungsweise: $\lambda \approx {\frac {G}{A}}\cdot k\Leftrightarrow k\approx {\frac {\lambda }{\frac {G}{A}}}$ .

1. Fall: Verdopplung innerhalb des exponentiellen Wachstums

Liegt die Verdopplung des Anfangsbestandes in der Phase des exponentiellen Wachstums, vereinfacht das die Rechnung erheblich. Hier wird der wahre Anfangsbestand $A$ normiert:

$f(0)=1[A]$ ; ebenso wird die Zeitachse auf den Verdopplungszeitraum $t_{D}$ normiert: $f(1[t_{D}])=2[A]$ . Es ergibt sich eine Wachstumsfunktion mit $\lambda =\ln {\frac {f(t_{D})}{A=1}}=\ln \left(2\right)\approx 0{,}693$ :

$y(t/t_{D})[A]=e^{\ln \left(2\right)\cdot t}|\lambda =\ln \left(2\right)$

Als Nächstes wird eine Obergrenze $G[A]$ als Vielfaches des Anfangsbestandes $A$ festgelegt und der Verdopplungspunkt eingesetzt:

${\begin{aligned}f(t/t_{D})[A]=2[A]&=G\cdot {\frac {1}{1+e^{-k\cdot G\cdot 1[t_{D}]}\cdot \left({\frac {G}{A=1}}-1\right)}}\\\Leftrightarrow e^{-k\cdot G}&={\frac {{\frac {G}{2[A=1]}}-1}{G-1}}\\\Leftrightarrow k&=-{\frac {\ln \left({\frac {{\frac {G}{2}}-1}{G-1}}\right)}{G}}\end{aligned}}$

Beispiel Obergrenze $G=100\cdot [{\textrm {Anfangsbestand}}]$ : ${\begin{aligned}\lambda &=\ln(2)&\approx 0{,}6963\\k&=-{\frac {\ln {\frac {49}{99}}}{100}}&\approx 0{,}007033\\{\frac {\lambda }{k}}&={\frac {0{,}6963}{0{,}007033}}=98{,}556&\approx G[A]\end{aligned}}$

2. Fall: Verdopplung außerhalb des exponentiellen Wachstums

Nur unwesentlich schwieriger wird der Fall, wenn die Verdopplungszeit schon außerhalb des exponentiellen Wachstums liegt; beispielsweise kann $G=2$ sein. Damit ist der zweite Referenzpunkt $P(T|Y)$ nicht mehr $y(t/[t_{D}])=2[A]$ :

${\begin{aligned}Y[A]&=1[A]\cdot e^{\lambda \cdot T}\\\Leftrightarrow \lambda &={\frac {\ln {\frac {Y}{A=1}}}{T}}={\frac {\ln(Y)}{T}}\end{aligned}}$

${\begin{aligned}Y[A]&=G\cdot {\frac {1}{1+e^{-k\cdot G\cdot T}\cdot \left(G-1\right)}}\\\Leftrightarrow e^{-k\cdot G\cdot T}&={\frac {{\frac {G}{Y}}-1}{G-1}}\\\Leftrightarrow k&=-{\frac {\ln \left({\frac {{\frac {G}{Y}}-1}{G-1}}\right)}{G\cdot T}}\end{aligned}}$

Zahlenbeispiel (extra krumme Zahlen):

Ein Kunde der FNORD-Bank legt einen Betrag von $\ln(2)$ [ÖGE] (örtliche Geld-Einheiten) an. Er bekommt einen Kontoauszug, der nach $e$ [NERD]-Zeiteinheiten einen Bestand von ${\sqrt {2}}$ [ÖGE] ausweist.

a) wie hoch ist der Faktor $\lambda$ bei stetiger Verzinsung?

b) aus ethischen Gründen setzt die FNORD-Bank eine Obergrenze von $4\cdot \pi$ [ÖGE] je Konto und setzt die Verzinsung logistisch. Wie hoch ist jetzt der Faktor $k$ der logistischen Funktion?

Lösung:

Der Kontostand zum Zeitpunkt T beträgt ${\frac {\sqrt {2}}{\ln {2}}}\approx 2{,}04028[A]$

${\begin{aligned}\lambda &={\frac {\ln(2{,}04028)}{e^{1}}}\\&\approx 0{,}262330\\\Rightarrow Y(t)&=\ln(2)\cdot e^{0{,}262330\cdot t}\\&\approx 0{,}693147\cdot e^{0{,}262330\cdot t}\end{aligned}}$

Die Obergrenze beträgt ${\frac {4\cdot \pi }{\ln {2}}}\approx 18{,}1294\cdot [A]$

${\begin{aligned}k&=-{\frac {\ln \left({\frac {{\frac {18{,}1294}{2{,}04028}}-1}{18{,}1294-1}}\right)}{18{,}1294\cdot e^{1}}}\\&\approx 0{,}0157412\\\Rightarrow Y(t)&=4\pi \cdot {\frac {1}{1+e^{-0{,}0157412\cdot 4\pi \cdot t}\cdot \left({\frac {4\pi }{ln(2)}}-1\right)}}\\&\approx 12{,}56644\cdot {\frac {1}{1+e^{-0{,}0157412\cdot 12{,}56644\cdot t}\cdot \left(17{,}1294\right)}}\end{aligned}}$

${\begin{aligned}{\frac {\lambda }{k}}&={\frac {0{,}262330}{0{,}0157412}}\\=16{,}6652&\approx 18{,}1294\\\approx {\frac {4\cdot \pi }{\ln {2}}}&={\frac {G}{A}}\end{aligned}}$

Siehe auch

Logistische Regression

Literatur

Nicholas F. Britton: Essential Mathematical Biology. 3. printing. Springer, London u. a. 2005, ISBN 1-85233-536-X, (Springer undergraduate mathematics series).
Norman R. Draper, Harry Smith: Applied Regression Analysis. 3rd Edition. Wiley-Interscience, New York NY u. a. 1998, ISBN 0-471-17082-8, (Wiley Series in Probability and Statistics. Texts and References Section).
Volker Oppitz, Volker Nollau: Taschenbuch Wirtschaftlichkeitsrechnung. Quantitative Methoden der ökonomischen Analyse. Carl Hanser Verlag, München u. a. 2004, ISBN 3-446-22463-7.
Volker Oppitz: Gabler-Lexikon Wirtschaftlichkeitsrechnung. Mit Anwendersoftware für Praxis und Studium. Gabler-Verlag Wiesbaden 1995, ISBN 3-409-19951-9.
Peter Schönfeld: Methoden der Ökonometrie. 2 Bände. Vahlen, Berlin u. a. 1969–1971.

Basierend auf einem Artikel in:

Wikipedia.de