Injektives Objekt

Injektives Objekt ist ein Begriff aus dem mathematischen Teilgebiet der Kategorientheorie.

Definition

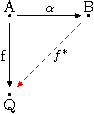
In einer Kategorie ${\mathcal {C}}$ heißt ein Objekt injektiv, wenn es zu jedem Monomorphismus $\alpha \colon A\rightarrow B$ und jedem $f\colon A\rightarrow Q$ ein $f^{*}\colon B\rightarrow Q$ gibt, so dass $f^{*}\circ \alpha =f$ ist.

Demnach ist genau dann injektiv, wenn für alle Monomorphismen $\alpha \colon A\rightarrow B$ die induzierte Abbildung $\mathrm {Mor} _{\mathcal {C}}(B,Q)\ni g\mapsto g\circ \alpha \in \mathrm {Mor} _{\mathcal {C}}(A,Q)$ surjektiv ist.

Beispiele

In der Kategorie der Mengen Me ist jede Menge injektiv.
Injektive Objekte in der Kategorie der abelschen Gruppen sind die teilbaren Gruppen, d.h. diejenigen Gruppen, für die die Multiplikation mit einer ganzen Zahl ungleich Null surjektiv ist; Beispiele sind $\mathbb {Q}$ und $\mathbb {Q} /\mathbb {Z}$ .
In der Kategorie der Vektorräume über einem Körper ist jedes Objekt injektiv.
Jedes terminale Objekt in einer Kategorie ist injektiv.
Ist $(Q_{i}|i\in I)$ eine Familie von injektiven Objekten, so ist das Produkt dieser Familie injektiv, falls es existiert.
Hat die Kategorie ein Nullobjekt, so ist ein Produkt von injektiven Objekten genau dann injektiv, wenn jedes $Q_{i}$ injektiv ist.
Ist injektiv, so ist jeder Monomorphismus $\alpha \colon Q\rightarrow P$ ein Schnitt (Das heißt, es gibt ein $\beta \colon P\rightarrow Q$ mit $\beta \circ \alpha =\mathbf {1} _{Q}$ ).
In der Kategorie der topologischen Räume ist die Menge $\{-1,1\}$ nicht injektiv, denn die Inklusionsabbildung $\{-1,1\}\rightarrow \mathbb {R}$ ist kein Schnitt. Es gibt keine stetige surjektive Funktion $\beta \colon \mathbb {R} \rightarrow \{-1,1\}$ . Dies ist eine Folgerung aus dem Zwischenwertsatz.

Injektive Moduln

Für einen Rechtsmodul über einem Ring sind die folgenden Aussagen äquivalent.

ist in der Kategorie der Rechtsmoduln injektiv.
Für jeden Monomorphismus $\alpha \colon Q\rightarrow M$ gibt es ein $\beta \colon M\rightarrow Q$ mit $\beta \circ \alpha =\mathbf {1} _{Q}$ . Dabei ist $\mathbf {1} _{Q}$ die Identität auf .
Baersches Kriterium: Für jedes Rechtsideal ${\mathfrak {a}}\hookrightarrow R$ und jedem Homomorphismus $f\colon {\mathfrak {a}}\rightarrow Q$ gibt es ein $f^{*}\colon R\rightarrow Q$ , so dass $f^{*}\circ \iota =f$ ist.

Injektive Moduln wurden 1940 von Reinhold Baer eingeführt, der allerdings das Adjektiv complete (d.h. vollständig) statt injektiv verwendete. Die deutsche Bezeichnung injektiver Modul lässt sich 1953 belegen.

Beispiele

Ein Ring ist halbeinfach genau dann, wenn jeder Modul über dem Ring injektiv ist. Daher ist jeder Vektorraum über einem Schiefkörper injektiv. Aus dem Baerschen Kriterium ergibt sich, dass über Hauptidealringen genau die teilbaren Moduln injektiv sind. Dabei ist ein Modul teilbar genau dann, wenn $Q\cdot r=Q$ ist für alle Ringelemente .
Ist $(Q_{i}|i\in I)$ eine Familie von Moduln, so ist das direkte Produkt der Familie genau dann injektiv, wenn jedes $Q_{i}$ injektiv ist.
Ein Ring ist noethersch genau dann, wenn die direkte Summe von injektiven Moduln injektiv ist. Dies ist eine Verallgemeinerung der entsprechenden Aussage über teilbare abelsche Gruppen.
Über einem erblichen (hereditären) Ring ist jedes epimorphe Bild eines injektiven Moduls injektiv. Dies ist eine Verallgemeinerung des entsprechenden Satzes über teilbare Gruppen.
Über einem Integritätsring ist ein torsionsfreier Modul genau dann injektiv, wenn er teilbar ist.
Ist $\rho \colon S\rightarrow R$ ein unitärer Ringhomomorphismus, so ist auf beiden Seiten ein S- Modul. Ist ein weiterer S- Modul, so trägt die Menge der S-Homomorphismen $\operatorname {Hom} _{S}(R,Q)$ auf der rechten Seite eine R-Modulstruktur durch $(\alpha \cdot r)(x)\colon =\alpha (r\cdot x)$ . Es gilt: Ist als S Modul injektiv, so ist $\operatorname {Hom} _{S}(R,Q)$ ein injektiver R-Modul. Besonders wichtig ist dies im Fall $S=\mathbb {Z}$ . Ist eine teilbare Gruppe, also als $\Z$ -Modul injektiv, so ist $\operatorname {Hom} _{\mathbb {Z} }(R,D)$ ein injektiver R-Modul.

Es gibt genügend viele injektive Moduln

Jeder Modul kann monomorph in einen injektiven Modul abgebildet werden.

Injektive Hülle

Ein Untermodul $U\hookrightarrow Q$ heißt groß , wenn $\{0\}$ der einzige Untermodul von ist, der mit den Durchschnitt $\{0\}$ hat. Ein Monomorphismus $\alpha :M\rightarrow Q$ heißt wesentlich, wenn $\alpha (M)$ groß in ist. Es gilt:

Jeder Modul kann wesentlich in einen injektiven Modul abgebildet werden. Der Modul ist durch diese Eigenschaft bis auf Isomorphie eindeutig bestimmt. Er heißt injektive Hülle von M und wird oft mit $I(M)$ bezeichnet.

Unzerlegbare injektive Moduln

Ein Modul heißt direkt unzerlegbar, wenn er nicht direkte Summe zweier Untermoduln ungleich Null ist. Für einen Modul sind folgende Aussagen äquivalent.

Jeder Untermodul ungleich dem Nullmodul ist groß in .
Die injektive Hülle $I(M)$ ist direkt unzerlegbar.
$I(M)$ ist die injektive Hülle eines jeden Untermoduls ungleich Null.
Der Endomorphismenring von $I(M)$ ist lokal.

Ein Modul, der die äquivalenten Eigenschaften des Satzes erfüllt heißt uniform . wird dann oft auch irreduzibel (durchschnittsirreduzibel) genannt.

Beispiele

Jeder einfache Modul ist uniform, besitzt also eine direkt unzerlegbare injektive Hülle.
Ist ${\mathfrak {p}}\hookrightarrow R$ ein Primideal in dem kommutative Ring , so ist $R/{\mathfrak {p}}$ uniform. Insbesondere ist jeder Integritätsring uniform als Modul.

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de