Modulraum

In der Mathematik bezeichnet man einen geometrischen Raum, dessen Punkte den verschiedenen mathematischen Objekten eines bestimmten Typs entsprechen, als Modulraum dieser Objekte.

Beispielsweise ist die projektive Ebene $\mathbb {R} P^{2}$ der Modulraum aller Geraden durch den Nullpunkt im $\mathbb {R} ^{3}$ . Der Modulraum der elliptischen Kurven über $\mathbb {C}$ ist die Modulkurve $SL(2,\mathbb {Z} )/H^{2}$

In der algebraischen Geometrie hat man für die Klassifikation algebraisch-geometrischer Objekte die Definitionen eines feinen Modulraums und eines groben Modulraums. Der feine Modulraum hat bessere Eigenschaften, existiert aber nicht immer.

Daneben spricht man auch in anderen Gebieten der Mathematik von Modulräumen mathematischer Objekte, ohne dass es für diesen Begriff eine einheitliche Definition gäbe. Beispielsweise ist in der symplektischen Geometrie der Modulraum der pseudoholomorphen Kurven von großer Bedeutung oder in der Teichmüller-Theorie der Modulraum hyperbolischer Metriken.

Beispiel

Die projektive Ebene $\mathbb {R} P^{2}$ ist per Definition die Menge der 1-dimensionalen Unterräume des Vektorraums $\mathbb {R} ^{3}$ . Sie lässt sich mit einem differenzierbaren Atlas versehen, so dass durch eine differenzierbare Mannigfaltigkeit parametrisierte Familien 1-dimensionaler Unterräume des $\mathbb {R} ^{3}$ gerade den differenzierbaren Abbildungen $X\to \mathbb {R} P^{2}$ entsprechen, die Punkten $x\in X$ jeweils die dem Parameter entsprechende Gerade in $\mathbb {R} ^{3}$ , also einen Punkt $L(x)\in \mathbb {R} P^{2}$ zuordnen.

Ähnlich lassen sich projektive Räume als Modulräume 1-dimensionaler Unterräume eines $\mathbb {R} ^{n}$ und allgemeiner Graßmann-Mannigfaltigkeiten als Modulräume k-dimensionaler Unterräume eines $\mathbb {R} ^{n}$ interpretieren.

Modulräume in der algebraischen Geometrie: Definitionen

Feiner Modulraum

Sei ein Funktor von der Kategorie der Schemata in die Kategorie der Mengen, der jedem Schema die Menge der Familien gewisser geometrischer Objekte mit Basis zuordnet. Dann ist der feine Modulraum für den Funktor , wenn es einen Isomorphismus

$\tau \colon F\to \operatorname {Hom} (\cdot ,M)$

gibt.

Die universelle Familie ist die Familie über , die der Identitätsabbildung $id_{M}\in \operatorname {Hom} (M,M)$ entspricht.

Grober Modulraum

Sei ein Funktor von der Kategorie der Schemata in die Kategorie der Mengen, der jedem Schema die Menge der Familien gewisser geometrischer Objekte mit Basis zuordnet. Dann ist ein grober Modulraum für den Funktor , wenn es eine natürliche Transformation

$\tau \colon F\to \operatorname {Hom} (\cdot ,M)$

gibt, die universell bzgl. aller natürlichen Transformationen ist.

Zu einem groben Modulraum gibt es im Allgemeinen keine universelle Familie.

Beispiele

Möbiusband als 1-dimensionales Vektorbündel über dem Kreis

Der feine Modulraum der Äquivalenzklassen endlicher Mengen modulo Bijektion ist die Menge der natürlichen Zahlen $\mathbb {N}$ .
Der feine Modulraum 1-dimensionaler Unterräume des $\mathbb {R} ^{3}$ ist die projektive Ebene.
Es gibt bis auf Isomorphismus nur einen 1-dimensionalen Vektorraum und tatsächlich ist der Punkt ein grober Modulraum 1-dimensionaler Vektorräume. Er ist aber kein feiner Modulraum, denn das Möbiusband als 1-dimensionales Vektorbündel über dem Kreis entspricht keiner Abbildung $S^{1}\to \left\{Punkt\right\}$ . Der Punkt ist aber ein feiner Modulraum für die Äquivalenzklassen $(V,1)$ aus einem 1-dimensionalen Vektorraum und einem von $0$ verschiedenen Element $1\in V$ , denn das Möbiusband als 1-dimensionales Vektorbündel hat keinen Schnitt ohne Nullstellen.

4-Tupel von Punkten auf der projektiven Geraden

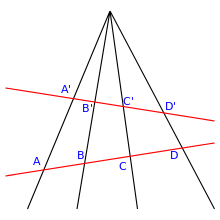
Das Doppelverhältnis bleibt unter projektiven Automorphismen erhalten.

Der feine Modulraum für die Quadrupel paarweise verschiedener Punkte auf der projektiven Geraden $P^{1}$ ist offensichtlich $(P^{1}\times P^{1}\times P^{1}\times P^{1})\setminus Diagonalen$ .

Die universelle Familie ist eine Teilmenge von $Q\times P^{1}$ , nämlich die Vereinigung der Bilder der durch $\sigma _{i}(p)=(p,p_{i})$ für $p=(p_{1},p_{2},p_{3},p_{4})$ gegebenen Schnitte $\sigma _{1},\ldots ,\sigma _{4}\colon Q\to Q\times P^{1}$ .

Zwei Quadrupel heißen projektiv äquivalent, wenn es einen projektiven Automorphismus $A\in PGL_{2}$ gibt, der das eine Quadrupel auf das andere abbildet. Bekanntlich ist das Doppelverhältnis eines Quadrupels paarweise verschiedener Punkte ein Element aus $P^{1}\setminus \left\{0,1,\infty \right\}$ und zwei solche Quadrupel sind genau dann projektiv äquivalent, wenn sie dasselbe Doppelverhältnis haben. Daraus kann man leicht herleiten, dass $P^{1}\setminus \left\{0,1,\infty \right\}$ der feine Modulraum für Quadrupel modulo projektiver Äquivalenz und $(P^{1}\setminus \left\{0,1,\infty \right\})\times P^{1}$ die universelle Familie ist.

Modulräume in anderen Gebieten der Mathematik

Modulraum der Riemannschen Metriken auf einer differenzierbaren Mannigfaltigkeit
Modulraum der pseudoholomorphen Kurven in einer symplektischen Mannigfaltigkeit
Modulraum der flachen Zusammenhänge eines Prinzipalbündels

Basierend auf einem Artikel in:

Wikipedia.de