Methode der kleinsten Quadrate

Die Methode der kleinsten Quadrate (kurz KQ-Methode) ist das mathematische Standardverfahren zur Ausgleichungsrechnung. Dabei wird zu einer Datenpunktwolke eine Kurve gesucht, die möglichst nahe an den Datenpunkten verläuft. Die Daten können physikalische Messwerte, wirtschaftliche Größen oder Ähnliches repräsentieren, während die Kurve aus einer parameterabhängigen problemangepassten Familie von Funktionen stammt. Die Methode der kleinsten Quadrate besteht dann darin, die Kurvenparameter so zu bestimmen, dass die Summe der quadratischen Abweichungen der Kurve von den beobachteten Punkten minimiert wird. Die Abweichungen werden Residuen genannt.

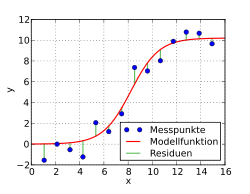
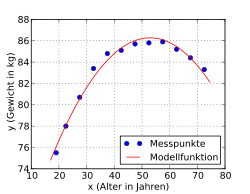
In der Beispielgrafik sind Datenpunkte eingetragen. In einem ersten Schritt wird eine Funktionenklasse ausgewählt, die zu dem Problem und den Daten passen sollte, hier eine logistische Funktion. Deren Parameter werden nun so bestimmt, dass die Summe der Quadrate der Abweichungen der Beobachtungen zu den Werten der Funktion minimiert wird. In der Grafik ist die Abweichung an der Stelle als senkrechter Abstand der Beobachtung von der Kurve zu erkennen.

Messpunkte und deren Abstand zu einer nach der Methode der kleinsten Quadrate bestimmten Funktion. Hier wurde eine logistische Funktion als Modellkurve gewählt.

In der Stochastik wird die Methode der kleinsten Quadrate meistens als Schätzmethode in der Regressionsanalyse benutzt, wo sie auch als Kleinste-Quadrate-Schätzung bezeichnet wird. Angewandt als Systemidentifikation ist die Methode der kleinsten Quadrate in Verbindung mit Modellversuchen z.B. für Ingenieure ein Ausweg aus der paradoxen Situation, Modellparameter für unbekannte Gesetzmäßigkeiten zu bestimmen.

Geschichte

Carl Friedrich Gauß

Piazzis Beobachtungen veröffentlicht in der Monatlichen Correspondenz vom September 1801

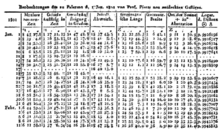
Am Neujahrstag 1801 entdeckte der italienische Astronom Giuseppe Piazzi den Zwergplaneten Ceres. 40 Tage lang konnte er die Bahn verfolgen, dann verschwand Ceres hinter der Sonne. Im Laufe des Jahres versuchten viele Wissenschaftler erfolglos, anhand von Piazzis Beobachtungen die Bahn zu berechnen – unter der Annahme einer Kreisbahn, denn nur für solche konnten damals die Bahnelemente aus beobachteten Himmelspositionen mathematisch ermittelt werden. Der 24-jährige Gauß hingegen konnte auch elliptische Bahnen aus drei Einzelbeobachtungen berechnen. Seine ersten Berechnungen waren noch ohne die Methode der kleinsten Quadrate, erst als nach der Wiederentdeckung von Ceres viele neue Daten vorlagen, benutzte er diese für eine genauere Bestimmung der Bahnelemente, ohne aber Details seiner Methode offenzulegen. Als Franz Xaver von Zach und Heinrich Wilhelm Olbers im Dezember 1801 den Kleinplaneten genau an dem von Gauß vorhergesagten Ort wiederfanden, war das nicht nur ein großer Erfolg für Gauß: Piazzis Ruf, der aufgrund seiner nicht zu einer Kreisbahn passen wollenden Bahnpunkte stark gelitten hatte, war ebenfalls wiederhergestellt.

Die Grundlagen der Methode derkleinsten Quadrate hatte Gauß schon 1795 im Alter von 18 Jahren entwickelt. Basis war eine Idee von Pierre-Simon Laplace, die Beträge von Fehlern aufzusummieren, so dass sich die Fehler zu Null addieren. Gauß nahm stattdessen die Fehlerquadrate und konnte die Nullsummen-Anforderung an die Fehler weglassen. Unabhängig davon entwickelte der Franzose Adrien-Marie Legendre dieselbe Methode und veröffentlichte darüber als Erster im Jahr 1805 am Schluss eines kleinen Werkes über die Berechnung der Kometenbahnen und veröffentlichte eine zweite Abhandlung darüber im Jahr 1810. Seine Darstellung war überaus klar und einfach. Von ihm stammt der Name Méthode des moindres carrés (Methode der kleinsten Quadrate).

1809 publizierte Gauß dann im zweiten Band seines himmelsmechanischen Werkes Theoria motus corporum coelestium in sectionibus conicis solem ambientium (Theorie der Bewegung der Himmelskörper, welche in Kegelschnitten die Sonne umlaufen) das Verfahren, inklusive der Normalgleichungen und des Gaußschen Eliminationsverfahrens sowie dem Gauß-Newton-Verfahren, womit er weit über Legendre hinausging. Dabei bezeichnete er es als sein Verfahren und erwähnte, dass er es schon im Jahr 1795 (also vor Legendre) entdeckt und benutzt habe, was Legendre nachhaltig verärgerte. Er beschwerte sich in einem langen Brief an Gauß über dessen Vorgehen, worauf Gauß nie antwortete. Gauß verwies nur gelegentlich auf einen Eintrag in seinem mathematischen Tagebuch vom 17. Juni 1798 (dort findet sich der kryptische Satz in Latein: Calculus probabilitatis contra La Place defensus (Kalkül der Wahrscheinlichkeit gegen Laplace verteidigt) und sonst nichts). Laplace beurteilte die Sache so, dass Legendre die Erstveröffentlichung tätigte, Gauß die Methode aber zweifelsfrei schon vorher kannte, selbst nutzte und auch anderen Astronomen brieflich mitteilte. Die Methode der kleinsten Quadrate wurde nun schnell das Standardverfahren zur Behandlung von astronomischen oder geodätischen Datensätzen.

Gauß benutzte dann das Verfahren intensiv bei seiner Vermessung des Königreichs Hannover durch Triangulation. 1821 und 1823 erschien die zweiteilige Arbeit sowie 1826 eine Ergänzung zur Theoria combinationis observationum erroribus minimis obnoxiae (Theorie der den kleinsten Fehlern unterworfenen Kombination der Beobachtungen), in denen Gauß eine Begründung liefern konnte, weshalb sein Verfahren im Vergleich zu den anderen so erfolgreich war: Die Methode der kleinsten Quadrate ist in einer breiten Hinsicht optimal, also besser als andere Methoden. Die genaue Aussage ist als der Satz von Gauß-Markow bekannt, da dieser Teil der Arbeit von Gauß wenig Beachtung fand und schließlich im 20. Jahrhundert von Andrei Andrejewitsch Markow wiederentdeckt und bekannt gemacht wurde. Die Theoria Combinationis enthält ferner wesentliche Fortschritte beim effizienten Lösen der auftretenden linearen Gleichungssysteme, wie das Gauß-Seidel-Verfahren und die LR-Zerlegung.

Der französische Vermessungsoffizier André-Louis Cholesky entwickelte während des Ersten Weltkriegs die Cholesky-Zerlegung, die gegenüber den Lösungsverfahren von Gauß nochmal einen erheblichen Effizienzgewinn darstellte. In den 1960er Jahren entwickelte Gene Golub die Idee, die auftretenden linearen Gleichungssysteme mittels QR-Zerlegung zu lösen.

Das Verfahren

Voraussetzungen

Man betrachtet eine abhängige Größe , die von einer Variablen oder auch von mehreren Variablen beeinflusst wird. So hängt die Dehnung einer Feder nur von der aufgebrachten Kraft ab, der Gewinn eines Unternehmens jedoch von mehreren Faktoren wie Umsatz, den verschiedenen Kosten oder dem Eigenkapital. Zur Vereinfachung der Notation wird im Folgenden die Darstellung auf eine Variable beschränkt. Der Zusammenhang zwischen und den Variablen wird über eine Modellfunktion , beispielsweise einer Parabel oder einer Exponentialfunktion

$y(x)=f(x;\alpha _{1},\dots ,\alpha _{m})$ ,

die von sowie von Funktionsparametern $\alpha _{j}$ abhängt, modelliert. Diese Funktion entstammt entweder der Kenntnis des Anwenders oder einer mehr oder weniger aufwendigen Suche nach einem Modell, eventuell müssen dazu verschiedene Modellfunktionen angesetzt und die Ergebnisse verglichen werden. Ein einfacher Fall auf Basis bereits vorhandener Kenntnis ist beispielsweise die Feder, denn hier ist das Hooksche Gesetz und damit eine lineare Funktion mit der Federkonstanten als einzigem Parameter Modellvoraussetzung. In schwierigeren Fällen, wie dem des Unternehmens muss der Wahl des Funktionstyps jedoch ein komplexer Modellierungsprozess vorausgehen.

Um Informationen über die Parameter und damit die konkrete Art des Zusammenhangs zu erhalten, werden zu jeweils gegebenen Werten $x_{i}$ der unabhängigen Variablen entsprechende Beobachtungswerte $y_{i}$ $(i=1,\dotsc ,n)$ erhoben. Die Parameter $\alpha _{j}$ dienen zur Anpassung des gewählten Funktionstyps an diese beobachteten Werte $y_{i}$ . Ziel ist es nun, die Parameter $\alpha _{j}$ so zu wählen, dass die Modellfunktion die Daten bestmöglich approximiert.

Gauß und Legendre hatten die Idee, Verteilungsannahmen über die Messfehler dieser Beobachtungswerte zu machen. Sie sollten im Durchschnitt Null sein, eine gleichbleibende Varianz haben und von jedem anderen Messfehler stochastisch unabhängig sein. Man verlangt damit, dass in den Messfehlern keinerlei systematische Information mehr steckt, sie also rein zufällig um Null schwanken. Außerdem sollten die Messfehler normalverteilt sein, was zum einen wahrscheinlichkeitstheoretische Vorteile hat und zum anderen garantiert, dass Ausreißer in so gut wie ausgeschlossen sind.

Um unter diesen Annahmen die Parameter $\alpha _{j}$ zu bestimmen, ist es im Allgemeinen notwendig, dass deutlich mehr Datenpunkte als Parameter vorliegen, es muss also n>m gelten.

Minimierung der Summe der Fehlerquadrate

Das Kriterium zur Bestimmung der Approximation sollte so gewählt werden, dass große Abweichungen der Modellfunktion von den Daten stärker gewichtet werden als kleine. Sofern keine Lösung ganz ohne Abweichungen möglich ist, dann ist der Kompromiss mit der insgesamt geringsten Abweichung das beste allgemein gültige Kriterium.

Dazu wird die Summe der Fehlerquadrate, die auch als Fehlerquadratsumme bezeichnet wird, als die Summe der quadrierten Differenzen zwischen den Werten der Modellkurve $f(x_{i})$ und den Daten $y_{i}$ definiert. In Formelschreibweise mit ${\vec {\alpha }}=(\alpha _{1},\alpha _{2},\dots ,\alpha _{m})\in \mathbb {R} ^{m}$ und ${\vec {f}}=(f(x_{1},{\vec {\alpha }}),\dots ,f(x_{n},{\vec {\alpha }}))\in \mathbb {R} ^{n}$ ergibt sich

$\sum _{i=1}^{n}(f(x_{i},{\vec {\alpha }})-y_{i})^{2}=\|{\vec {f}}-{\vec {y}}\|_{2}^{2}.$

Es sollen dann diejenigen Parameter $\alpha _{j}$ ausgewählt werden, bei denen die Summe der Fehlerquadrate minimal wird:

$\min _{\vec {\alpha }}\|{\vec {f}}-{\vec {y}}\|_{2}^{2}.$

Wie genau dieses Minimierungsproblem gelöst wird, hängt von der Art der Modellfunktion ab.

Wird die Fehlerquadratsumme für einen externen Datensatz vorhergesagt, so spricht man von der PRESS-Statistik (predictive residual sum of squares).

Lineare Modellfunktion

Lineare Modellfunktionen sind Linearkombinationen aus beliebigen, im Allgemeinen nicht-linearen Basisfunktionen. Für solche Modellfunktionen lässt sich das Minimierungsproblem auch analytisch über einen Extremwertansatz ohne iterative Annäherungsschritte lösen. Zunächst werden einige einfache Spezialfälle und Beispiele gezeigt.

Spezialfall einer einfachen linearen Ausgleichsgeraden

Herleitung und Verfahren

Eine einfache Modellfunktion mit zwei linearen Parametern stellt das Polynom erster Ordnung

$f(x)=\alpha _{0}+\alpha _{1}x.$

dar. Gesucht werden zu gegebenen Messwerten $(x_{1},y_{1}),\ldots ,(x_{n},y_{n})$ die Koeffizienten $\alpha _{0}$ und $\alpha _{1}$ der bestangepassten Geraden. Die Abweichungen $r_{i}$ zwischen der gesuchten Geraden und den jeweiligen Messwerten

${\begin{matrix}r_{1}=&\alpha _{0}+&\alpha _{1}x_{1}-y_{1}\\r_{2}=&\alpha _{0}+&\alpha _{1}x_{2}-y_{2}\\\vdots &\vdots &\vdots \\r_{n}=&\alpha _{0}+&\alpha _{1}x_{n}-y_{n}\\\end{matrix}}$

nennt man Anpassungsfehler oder Residuen. Gesucht sind nun die Koeffizienten $\alpha _{0}$ und $\alpha _{1}$ mit der kleinsten Summe der Fehlerquadrate

$\min _{\alpha _{0},\alpha _{1}}\sum _{i=1}^{n}r_{i}^{2}.$

Der große Vorteil des Ansatzes mit diesem Quadrat der Fehler wird sichtbar, wenn man diese Minimierung mathematisch durchführt: Die Summenfunktion wird als Funktion der beiden Variablen $\alpha _{0}$ und $\alpha _{1}$ aufgefasst (die eingehenden Messwerte sind dabei numerische Konstanten), dann die Ableitung (genauer: partielle Ableitungen) der Funktion nach diesen Variablen gebildet und von dieser Ableitung schließlich die Nullstelle gesucht. Es ergibt sich das lineare Gleichungssystem

${\begin{aligned}\textstyle n\cdot \alpha _{0}+\left(\sum \limits _{i=1}^{n}x_{i}\right)\alpha _{1}&=\textstyle \sum \limits _{i=1}^{n}y_{i}\\\textstyle \left(\sum \limits _{i=1}^{n}x_{i}\right)\alpha _{0}+\left(\sum \limits _{i=1}^{n}x_{i}^{2}\right)\alpha _{1}&=\textstyle \sum \limits _{i=1}^{n}x_{i}y_{i}\end{aligned}}$

mit der Lösung

$\alpha _{1}={\frac {\sum \nolimits _{i=1}^{n}(x_{i}-{\overline {x}})(y_{i}-{\overline {y}})}{\sum \nolimits _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}}={\frac {s_{x,y}}{s_{x,x}}}$ und $\;\alpha _{0}={\overline {y}}-\alpha _{1}{\overline {x}}\,$ ,

wobei $s_{x,y}$ die empirische Kovarianz und $s_{x,x}$ die empirische Varianz darstellt. Dabei ist $\textstyle {\overline {x}}={\frac {1}{n}}\sum \nolimits _{i=1}^{n}x_{i}$ das arithmetische Mittel der -Werte, ${\overline {y}}$ entsprechend. Die Lösung für $\alpha _{1}$ kann mit Hilfe des Verschiebungssatzes auch in nicht-zentrierter Form

$\alpha _{1}={\frac {\sum _{i=1}^{n}(x_{i}y_{i})-n{\overline {x}}{\overline {y}}}{\left(\sum _{i=1}^{n}x_{i}^{2}\right)-n{\overline {x}}^{2}}}$

angegeben werden. Diese Ergebnisse können auch mit Funktionen einer reellen Variablen, also ohne partielle Ableitungen, hergeleitet werden.

Beispiel mit einer Ausgleichsgeraden

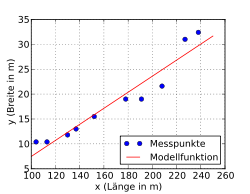
Streudiagramm von Längen und Breiten von 10 zufällig ausgewählten Kriegsschiffen

Folgendes Beispiel soll das Approximieren der linearen Funktion $f(x)=\alpha _{0}+\alpha _{1}x$ zeigen. Es wurden zufällig 10 Kriegsschiffe ausgewählt und bezüglich mehrerer Merkmale, darunter Länge (m) und Breite (m), analysiert. Es soll untersucht werden, ob die Breite eines Kriegsschiffs möglicherweise in einem festen Bezug zur Länge steht.

Das Streudiagramm zeigt, dass zwischen Länge und Breite eines Schiffs ein ausgeprägter linearer Zusammenhang besteht. Es wird also als Modellfunktion eine Ausgleichsgerade genommen und mit Hilfe der Methode der kleinsten Quadrate errechnet. Man erhält nun analog zum oben angegebenen Fall zunächst

${\overline {x}}={\frac {\sum \nolimits _{i=1}^{n}x_{i}}{n}}={\frac {1678}{10}}=167{,}8$

und entsprechend

${\overline {y}}=18{,}41.$

In der folgenden Tabelle sind die Daten zusammen mit den Zwischenergebnissen aufgeführt.

>	$x_{i}$	$y_{i}$	$x_{i}^{*}$	$y_{i}^{*}$	$x_{i}^{}\cdot y_{i}^{}$	$x_{i}^{}\cdot x_{i}^{}$
Nummer	Länge (m)	Breite (m)	$(x_{i}-{\overline {x}})$	$(y_{i}-{\overline {y}})$
1	208	21,6	40,2	3,19	128,238	1616,04
2	152	15,5	−15,8	−2,91	45,978	249,64
3	113	10,4	−54,8	−8,01	438,948	3003,04
4	227	31,0	59,2	12,59	745,328	3504,64
5	137	13,0	−30,8	−5,41	166,628	948,64
6	238	32,4	70,2	13,99	982,098	4928,04
7	178	19,0	10,2	0,59	6,018	104,04
8	104	10,4	−63,8	−8,01	511,038	4070,44
9	191	19,0	23,2	0,59	13,688	538,24
10	130	11,8	−37,8	−6,61	249,858	1428,84
Σ	1678	184,1	0,0	0,00	3287,820	20391,60

Damit bestimmt man $\alpha _{1}$ als

$\alpha _{1}={\frac {\sum \nolimits _{i=1}^{n}(x_{i}-{\overline {x}})(y_{i}-{\overline {y}})}{\sum \nolimits _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}}={\frac {3287{,}820}{20391{,}60}}=0{,}1612,$

so dass man sagen könnte, mit jedem Meter Länge wächst ein Kriegsschiff im Durchschnitt etwa 16 Zentimeter in die Breite. Das Absolutglied $\alpha _{0}$ ergibt sich als

$\alpha _{0}={\overline {y}}-\alpha _{1}{\overline {x}}=18{,}41-0{,}1612\cdot 167{,}8=-8{,}6451.$

Die Anpassung der Punkte ist recht gut. Im Mittel beträgt die Abweichung zwischen der vorhergesagten Breite mit Hilfe des Merkmals Länge und der beobachteten Breite 2,1 m. Auch das Bestimmtheitsmaß, als normierter Koeffizient, ergibt einen Wert von ca. 92 % (100 % würde einer mittleren Abweichung von 0 m entsprechen); zur Berechnung siehe das Beispiel zum Bestimmtheitsmaß.

Einfache polynomiale Ausgleichskurven

Streudiagramm: Durchschnittliches Gewicht von Männern nach Alter mit parabelförmiger Modellfunktion

Datensatz mit approximierenden Polynomen

Allgemeiner als eine lineare Ausgleichsgerade sind Ausgleichspolynome

$y(x)\approx \alpha _{0}+\alpha _{1}x+\alpha _{2}x^{2}+\ldots +\alpha _{q}x^{q},$

die nun anhand eines Beispiels illustriert werden (auch solche Ausgleichspolynomansätze lassen sich – zusätzlich zur iterativen Lösung – analytisch über einen Extremwertansatz lösen).

Als Ergebnisse der Mikrozensus-Befragung durch das statistische Bundesamt sind die durchschnittlichen Gewichte von Männern nach Altersklassen gegeben (Quelle: Statistisches Bundesamt, Wiesbaden 2009). Für die Analyse wurden die Altersklassen durch die Klassenmitten ersetzt. Es soll die Abhängigkeit der Variablen Gewicht () von der Variablen Alter () analysiert werden.

Das Streudiagramm lässt auf eine annähernd parabolische Beziehung zwischen und schließen, welche sich häufig gut durch ein Polynom annähern lässt. Es wird ein polynomialer Ansatz der Form

$y(x)\approx \alpha _{0}+\alpha _{1}x+\alpha _{2}x^{2}+\alpha _{3}x^{3}+\alpha _{4}x^{4}$

versucht. Als Lösung ergibt sich das Polynom 4. Grades

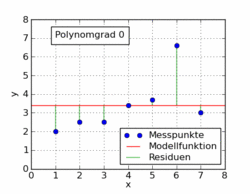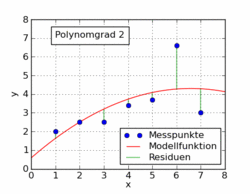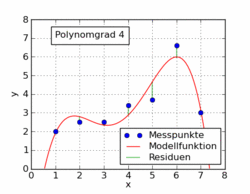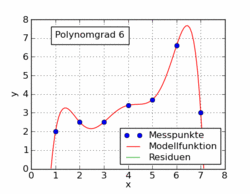
$y(x)\approx 47{,}86+2{,}2x-0{,}04809x^{2}+0{,}0004935x^{3}-0{,}000002148x^{4}$ .

Die Messpunkte weichen im Mittel (Standardabweichung) 0,19 kg von der Modellfunktion ab. Reduziert man den Grad des Polynoms auf 3, erhält man die Lösung

$y(x)\approx 54{,}22+1{,}515x-0{,}0226x^{2}+0{,}0001002x^{3}$

mit einer mittleren Abweichung von 0,22 kg und beim Polynomgrad 2 die Lösung

$y(x)\approx 61{,}42+0{,}9397x-0{,}008881x^{2}$

mit einer mittleren Abweichung von 0,42 kg. Wie zu erkennen ist, ändern sich beim Wegfallen der höheren Terme die Koeffizienten der niedrigeren Terme. Die Methode versucht, das Beste aus jeder Situation herauszuholen. Entsprechend werden die fehlenden höheren Terme mit Hilfe der niedrigeren Terme so gut wie möglich ausgeglichen, bis das mathematische Optimum erreicht ist. Mit dem Polynom zweiten Grades (Parabel) wird der Verlauf der Messpunkte noch sehr gut beschrieben (siehe Abbildung).

Spezialfall einer linearen Ausgleichsfunktion mit mehreren Variablen

Ist die Modellfunktion ein mehrdimensionales Polynom erster Ordnung, besitzt also statt nur einer Variablen mehrere unabhängige Modellvariablen $x_{1},\ldots ,x_{N}$ , erhält man eine lineare Funktion der Form

$f(x_{1},\ldots ,x_{N};\alpha _{0},\alpha _{1},\dots ,\alpha _{N})=\alpha _{0}+\alpha _{1}x_{1}+\ldots +\alpha _{N}x_{N}$

die auf die Residuen

${\begin{matrix}r_{1}=&\alpha _{0}+\alpha _{1}x_{1,1}+&\cdots \;\;+\alpha _{j}x_{j,1}+&\cdots \;\;+\alpha _{N}x_{N,1}-y_{1}\\r_{2}=&\alpha _{0}+\alpha _{1}x_{1,2}+&\cdots \;\;+\alpha _{j}x_{j,2}+&\cdots \;\;+\alpha _{N}x_{N,2}-y_{2}\\\vdots &\vdots &\vdots &\vdots \\r_{i}=&\alpha _{0}+\alpha _{1}x_{1,i}+&\cdots \;\;+\alpha _{j}x_{j,i}+&\cdots \;\;+\alpha _{N}x_{N,i}-y_{i}\\\vdots &\vdots &\vdots &\vdots \\r_{n}=&\alpha _{0}+\alpha _{1}x_{1,n}+&\cdots \;\;+\alpha _{j}x_{j,n}+&\cdots \;\;+\alpha _{N}x_{N,n}-y_{n}\\\end{matrix}}$

führt und über den Minimierungsansatz

$\min _{\alpha }\sum _{i=1}^{n}r_{i}^{2}$

gelöst werden kann.

Der allgemeine lineare Fall

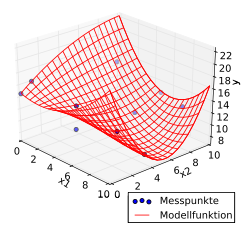
Zweidimensionale Polynomfläche zweiter Ordnung mit 3 × 3 = 9 Basisfunktionen:
f(x₁, x₂) = $\alpha$ ₀ + $\alpha$ ₁x₁¹ + $\alpha$ ₂x₁² + $\alpha$ ₃x₂¹ + $\alpha$ ₄x₁¹x₂¹ + $\alpha$ ₅x₁²x₂¹ + $\alpha$ ₆x₂² + $\alpha$ ₇x₁¹x₂² + $\alpha$ ₈x₁²x₂²

Im Folgenden soll der allgemeine Fall von beliebigen linearen Modellfunktionen mit beliebiger Dimension gezeigt werden. Zu einer gegebenen -dimensionalen Messwertfunktion

$y(x_{1},x_{2},\dots ,x_{N})$

mit unabhängigen Variablen sei eine optimal angepasste lineare Modellfunktion

$f(x_{1},x_{2},\dots ,x_{N};\alpha _{1},\alpha _{2},\dots ,\alpha _{m})=\sum _{j=1}^{m}\alpha _{j}\varphi _{j}(x_{1},x_{2},\dots ,x_{N})$

gesucht, deren quadratische Abweichung dazu minimal sein soll. $x_{i}$ sind dabei die Funktionskoordinaten, $\alpha _{j}$ die zu bestimmenden linear eingehenden Parameter und $\varphi _{j}$ beliebige zur Anpassung an das Problem gewählte linear unabhängige Funktionen.

Bei gegebenen Messpunkten

$(x_{1,1},x_{2,1},\dots ,x_{N,1};y_{1}),(x_{1,2},x_{2,2},\dots ,x_{N,2};y_{2}),\dots ,(x_{1,n},x_{2,n},\dots ,x_{N,n};y_{n})$

erhält man die Anpassungsfehler

${\begin{matrix}r_{1}=&\alpha _{0}\varphi _{0}(x_{1,1},\dots ,x_{N,1})\;\;+&\alpha _{1}\varphi _{1}(x_{1,1},\dots ,x_{N,1})+&\cdots \;\;\;+\alpha _{m}\varphi _{m}(x_{1,1},\dots ,x_{N,1})-y_{1}\\r_{2}=&\alpha _{0}\varphi _{0}(x_{1,2},\dots ,x_{N,2})\;\;+&\alpha _{1}\varphi _{1}(x_{1,2},\dots ,x_{N,2})+&\cdots \;\;\;+\alpha _{m}\varphi _{m}(x_{1,2},\dots ,x_{N,2})-y_{2}\\\vdots &\vdots &\vdots &\vdots \\r_{i}=&\alpha _{0}\varphi _{0}(x_{1,i},\dots ,x_{N,i})\;\;+&\alpha _{1}\varphi _{1}(x_{1,i},\dots ,x_{N,i})+&\cdots \;\;\;+\alpha _{m}\varphi _{m}(x_{1,i},\dots ,x_{N,i})-y_{i}\\\vdots &\vdots &\vdots &\vdots \\r_{n}=&\alpha _{0}\varphi _{0}(x_{1,n},\dots ,x_{N,n})\;\;+&\alpha _{1}\varphi _{1}(x_{1,n},\dots ,x_{N,n})+&\cdots \;\;\;+\alpha _{m}\varphi _{m}(x_{1,n},\dots ,x_{N,n})-y_{n}\\\end{matrix}}$

oder in Matrixschreibweise

$r=A\alpha -y,$

wobei der Vektor die $r_{i}$ zusammenfasst, die Matrix die Basisfunktionswerte $A_{ij}:=\varphi _{j}(x_{1,i},\dots ,x_{N,i})$ , der Parametervektor $\alpha$ die Parameter $\alpha _{j}$ und der Vektor die Beobachtungen $y_{i}$ .

Das Minimierungsproblem kann dann mithilfe der euklidischen Norm wie folgt formuliert werden:

$\min _{\alpha }\sum _{i=1}^{n}r_{i}^{2}=\min _{\alpha }\|f(\alpha )-y\|_{2}^{2}=\min _{\alpha }\|A\alpha -y\|_{2}^{2}$ .

Lösung des Minimierungsproblems

Herleitung und Verfahren

Das Minimierungsproblem ergibt sich wie im allgemeinen linearen Fall gezeigt als

$\min _{\alpha }\|A\alpha -y\|_{2}^{2}=\min _{\alpha }(A\alpha -y)^{T}(A\alpha -y)=\min _{\alpha }(\alpha ^{T}A^{T}A\alpha -2y^{T}A\alpha +y^{T}y).$

Dieses Problem ist immer lösbar. Hat die Matrix vollen Rang, so ist die Lösung sogar eindeutig. Die partiellen Ableitungen bezüglich der $\alpha _{j}$ und Nullsetzen derselben zum Bestimmen eines Extremums ergeben ein lineares System von Normalgleichungen (auch Normalengleichungen)

$A^{T}A\alpha =A^{T}y,$

das die Lösung des Minimierungsproblems liefert und im Allgemeinen numerisch gelöst werden muss. Die Matrix $A^{T}A$ ist positiv definit, so dass es sich beim gefundenen Extremum um ein Minimum handelt. Damit kann das Lösen des Minimierungsproblems der linearen Modellfunktionen auf das Lösen eines Gleichungssystems reduziert werden. Im einfachen Fall einer Ausgleichsgeraden kann dessen Lösung, wie gezeigt wurde, sogar direkt als einfache Formel angegeben werden.

Alternativ lassen sich die Normalgleichungen in der Darstellung

$A^{T}A\alpha -A^{T}y={\begin{pmatrix}\left\langle \varphi _{0},\varphi _{0}\right\rangle &\left\langle \varphi _{0},\varphi _{1}\right\rangle &\cdots &\left\langle \varphi _{0},\varphi _{m}\right\rangle \\\left\langle \varphi _{1},\varphi _{0}\right\rangle &\left\langle \varphi _{1},\varphi _{1}\right\rangle &\cdots &\left\langle \varphi _{1},\varphi _{m}\right\rangle \\\vdots &\vdots &\ddots &\vdots \\\left\langle \varphi _{m},\varphi _{0}\right\rangle &\left\langle \varphi _{m},\varphi _{1}\right\rangle &\cdots &\left\langle \varphi _{m},\varphi _{m}\right\rangle \\\end{pmatrix}}{\begin{pmatrix}\alpha _{0}\\\alpha _{1}\\\vdots \\\alpha _{m}\end{pmatrix}}-{\begin{pmatrix}\left\langle y,\varphi _{0}\right\rangle \\\left\langle y,\varphi _{1}\right\rangle \\\vdots \\\left\langle y,\varphi _{m}\right\rangle \\\end{pmatrix}}=0.$

ausschreiben, wobei $\left\langle \cdot ,\cdot \right\rangle$ das Standardskalarprodukt symbolisiert. Die Basisfunktionen $\varphi _{i}$ sind als Vektoren ${\vec {\varphi _{i}}}=(\varphi _{i}(x_{1,1},\dots ,x_{N,1}),\varphi _{i}(x_{1,2},\dots ,x_{N,2}),\ldots ,\varphi _{i}(x_{1,n},\dots ,x_{N,n}))$ zu lesen mit den diskreten Stützstellen am Ort der Beobachtungen $y={\vec {y}}=(y_{1},y_{2},\ldots ,y_{n})$ .

Ferner lässt sich das Minimierungsproblem mit einer Singulärwertzerlegung gut analysieren. Diese motivierte auch den Ausdruck der Pseudoinversen, einer Verallgemeinerung der normalen Inversen einer Matrix. Diese liefert dann eine Sichtweise auf nichtquadratische lineare Gleichungssysteme, die einen nicht stochastisch, sondern algebraisch motivierten Lösungsbegriff erlaubt.

Numerische Behandlung der Lösung

Zur numerischen Lösung des Problems gibt es zwei Wege. Zum einen können die Normalgleichungen

$A^{T}A\alpha =A^{T}y$

gelöst werden, die eindeutig lösbar sind, falls die Matrix vollen Rang hat. Ferner hat die Systemmatrix $A^{T}A$ die Eigenschaft, positiv definit zu sein, ihre Eigenwerte sind also alle positiv. Zusammen mit der Symmetrie von $A^{T}A$ kann dies beim Einsatz von numerischen Verfahren zur Lösung ausgenutzt werden: beispielsweise mit der Cholesky-Zerlegung oder dem CG-Verfahren. Da beide Methoden von der Kondition der Matrix stark beeinflusst werden, ist dies manchmal keine empfehlenswerte Herangehensweise: Ist schon A schlecht konditioniert, so ist $A^{T}A$ quadratisch schlecht konditioniert. Dies führt dazu, dass Rundungsfehler so weit verstärkt werden können, dass sie das Ergebnis unbrauchbar machen.

Zum anderen liefert das ursprüngliche Minimierungsproblem eine stabilere Alternative, da es bei kleinem Wert des Minimums eine Kondition in der Größenordnung der Kondition von A, bei großen Werten des Quadrats der Kondition von A hat. Um die Lösung zu berechnen wird eine QR-Zerlegung verwendet, die mit Householdertransformationen oder Givens-Rotationen erzeugt wird. Grundidee ist, dass orthogonale Transformationen die euklidische Norm eines Vektors nicht verändern. Damit ist

$\|A\alpha -y\|_{2}=\|Q(A\alpha -y)\|_{2}$

für jede orthogonale Matrix . Zur Lösung des Problems kann also eine QR-Zerlegung von berechnet werden, wobei man die rechte Seite direkt mittransformiert. Dies führt auf eine Form

$\|R\alpha -Q^{T}y\|_{2}$

mit $R={\begin{pmatrix}{\tilde {R}}\\0\end{pmatrix}},$ wobei ${\tilde {R}}\in \mathbb {R} ^{m\times m}$ eine rechte obere Dreiecksmatrix ist. Die Lösung des Problems ergibt sich somit durch die Lösung des Gleichungssystems

${\tilde {R}}{\begin{pmatrix}\alpha _{1}\\\vdots \\\alpha _{m}\end{pmatrix}}={\begin{pmatrix}(Q^{T}y)_{1}\\\vdots \\(Q^{T}y)_{m}\end{pmatrix}}.$

Die Norm des Minimums ergibt sich dann aus den restlichen Komponenten der transformierten rechten Seite $(Qy)_{m+1},\dots ,(Qy)_{n},$ da die dazugehörigen Gleichungen aufgrund der Nullzeilen in nie erfüllt werden können.

In der statistischen Regressionsanalyse spricht man bei mehreren gegebenen Variablen $x_{j}$ von multipler Regression. Der Ansatz ist auch als OLS (ordinary least squares) bekannt, im Gegensatz zu GLS (generalised least squares), dem multiplen linearen Regressionsmodell bei Fehlertermen, die von der Verteilungsannahme wie Unkorreliertheit und Homoskedastie abweichen. Dagegen liegen bei multivariater Regression für jede Beobachtung $(i=1,\dots ,n)$ viele -Werte vor, so dass statt eines Vektors eine $n\times r$ -Matrix vorliegt. Die linearen Regressionsmodelle sind in der Statistik wahrscheinlichkeitstheoretisch intensiv erforscht worden. Besonders in der Ökonometrie werden beispielsweise komplexe rekursiv definierte lineare Strukturgleichungen analysiert, um volkswirtschaftliche Systeme zu modellieren.

Probleme mit Nebenbedingungen

Häufig sind Zusatzinformationen an die Parameter bekannt, die durch Nebenbedingungen formuliert werden, die dann in Gleichungs- oder Ungleichungsform vorliegen. Gleichungen tauchen beispielsweise auf, wenn bestimmte Datenpunkte interpoliert werden sollen. Ungleichungen tauchen häufiger auf, in der Regel in der Form von Intervallen für einzelne Parameter. Im Einführungsbeispiel wurde die Federkonstante erwähnt, diese ist immer größer Null und kann für den konkret betrachteten Fall immer nach oben abgeschätzt werden.

Im Gleichungsfall können diese bei einem sinnvoll gestellten Problem genutzt werden, um das ursprüngliche Minimierungsproblem in eines einer niedrigereren Dimension umzuformen, dessen Lösung die Nebenbedingungen automatisch erfüllt.

Schwieriger ist der Ungleichungsfall. Hier ergibt sich bei linearen Ungleichungen das Problem

$\min _{\alpha }\|{\vec {f}}-{\vec {y}}\|_{2}\;$ mit $\;l\leq C\alpha \leq u$ , $C\in \mathbb {R} ^{n\times n},$

wobei die Ungleichungen komponentenweise gemeint sind. Dieses Problem ist als konvexes und quadratisches Optimierungsproblem eindeutig lösbar und kann beispielsweise mit Methoden zur Lösung solcher angegangen werden.

Quadratische Ungleichungen ergeben sich beispielsweise bei der Nutzung einer Tychonow-Regularisierung zur Lösung von Integralgleichungen. Die Lösbarkeit ist hier nicht immer gegeben. Die numerische Lösung kann beispielsweise mit speziellen QR-Zerlegungen erfolgen.

Nichtlineare Modellfunktionen

Grundgedanke und Verfahren

Mit dem Aufkommen leistungsfähiger Rechner gewinnt insbesondere die nichtlineare Regression an Bedeutung. Hierbei gehen die Parameter nichtlinear in die Funktion ein. Nichtlineare Modellierung ermöglicht im Prinzip die Anpassung von Daten an jede Gleichung der Form $y=f(\alpha )$ . Da diese Gleichungen Kurven definieren, werden die Begriffe nichtlineare Regression und „curve fitting“ zumeist synonym gebraucht.

Manche nichtlineare Probleme lassen sich durch geeignete Substitution in lineare überführen und sich dann wie oben lösen. Ein multiplikatives Modell von der Form

$y=\alpha _{0}\cdot x^{\alpha _{1}}$

lässt sich beispielsweise durch Logarithmieren in ein additives System überführen. Dieser Ansatz findet unter Anderem in der Wachstumstheorie Anwendung.

Im Allgemeinen ergibt sich bei nichtlinearen Modellfunktionen ein Problem der Form

$\min _{\alpha }\|f(\alpha )-y\|_{2},$

mit einer nichtlinearen Funktion . Partielle Differentiation ergibt dann ein System von Normalgleichungen, das nicht mehr analytisch gelöst werden kann. Eine numerische Lösung kann hier iterativ mit dem Gauß-Newton-Verfahren erfolgen. Jenes hat allerdings den Nachteil, dass die Konvergenz des Verfahrens nicht gesichert ist.

Aktuelle Programme arbeiten häufig mit einer Variante, dem Levenberg-Marquardt-Algorithmus. Bei diesem Verfahren ist zwar die Konvergenz ebenfalls nicht gesichert, jedoch wird durch eine Regularisierung die Monotonie der Näherungsfolge garantiert. Zudem ist das Verfahren bei größerer Abweichung der Schätzwerte toleranter als die Ursprungsmethode. Beide Verfahren sind mit dem Newton-Verfahren verwandt und konvergieren meist quadratisch, in jedem Schritt verdoppelt sich also die Zahl der korrekten Nachkommastellen.

Wenn die Differentiation auf Grund der Komplexität der Zielfunktion zu aufwändig ist, stehen eine Reihe anderer Verfahren als Ausweichlösung zu Verfügung, die keine Ableitungen benötigen, siehe bei Methoden der lokalen nichtlinearen Optimierung.

Fehlverhalten bei Nichterfüllung der Voraussetzungen

Die Methode der kleinsten Quadrate erlaubt es, unter bestimmten Voraussetzungen die wahrscheinlichsten aller Modellparameter zu berechnen. Dazu muss ein korrektes Modell gewählt worden sein, eine ausreichende Menge Messwerte vorliegen und die Abweichungen der Messwerte gegenüber dem Modellsystem müssen eine Normalverteilung bilden. In der Praxis kann die Methode jedoch auch bei Nichterfüllung dieser Voraussetzungen für diverse Zwecke eingesetzt werden. Dennoch sollte beachtet werden, dass die Methode der kleinsten Quadrate unter bestimmten ungünstigen Bedingungen völlig unerwünschte Ergebnisse liefern kann. Beispielsweise sollten keineAusreißer in den Messwerten vorliegen, da diese das Schätzergebnis verzerren. Außerdem ist Multikollinearität zwischen den zu schätzenden Parametern ungünstig, da diese numerische Probleme verursacht. Im Übrigen können auch Regressoren, die weit von den anderen entfernt liegen, die Ergebnisse der Ausgleichsrechnung stark beeinflussen. Man spricht hier von Werten mit großer Hebelkraft (High Leverage Value).

Multikollinearität

Multikollinearität entsteht, wenn die Messreihen zweier gegebener Variablen $x_{i}$ und $x_{j}$ sehr hoch korreliert sind, also fast linear abhängig sind. Im linearen Fall bedeutet dies, dass die Determinante der Normalgleichungsmatrix $A^{T}A$ sehr klein und die Norm der Inversen umgekehrt sehr groß, die Kondition von $A^{T}A$ ist also stark beeinträchtigt. Die Normalgleichungen sind dann numerisch schwer zu lösen. Die Lösungswerte können unplausibel groß werden und bereits kleine Änderungen in den Beobachtungen bewirken große Änderungen in den Schätzwerten.

Ausreißer

Ausreißer von y:
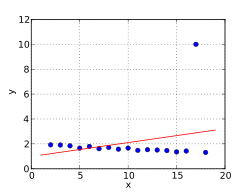
Der Wert zieht die Gerade nach oben

Als Ausreißer sind Datenwerte definiert, die „nicht in eine Messreihe passen“. Diese Werte beeinflussen die Berechnung der Parameter stark und verfälschen das Ergebnis. Um dies zu vermeiden, müssen die Daten auf fehlerhafte Beobachtungen untersucht werden. Die entdeckten Ausreißer können beispielsweise aus der Messreihe ausgeschieden werden oder es sind alternative ausreißerresistente Berechnungsverfahren wie gewichtete Regression oder das Drei-Gruppen-Verfahren anzuwenden.

Im ersten Fall wird nach der ersten Berechnung der Schätzwerte durch statistische Tests geprüft, ob Ausreißer in einzelnen Messwerten vorliegen. Diese Messwerte werden dann ausgeschieden und die Schätzwerte erneut berechnet. Dieses Verfahren eignet sich dann, wenn nur wenige Ausreißer vorliegen.

Bei der gewichteten Regression werden die abhängigen Variablen in Abhängigkeit von ihren Residuen gewichtet. Ausreißer, d.h. Beobachtungen mit großen Residuen, erhalten ein geringes Gewicht, das je nach Größe des Residuums abgestuft sein kann. Beim Algorithmus nach Frederick Mosteller und John W. Tukey (1977), der als „biweighting“ bezeichnet wird, werden unproblematische Werte mit 1 und Ausreißer mit 0 gewichtet, was die Unterdrückung des Ausreißers bedingt. Bei der gewichteten Regression sind in der Regel mehrere Iterationsschritte erforderlich, bis sich die Menge der erkannten Ausreißer nicht mehr ändert.

Verallgemeinerte Kleinste-Quadrate-Modelle

Weicht man die starken Anforderungen im Verfahren an die Residuen (Fehlerterme) auf, erhält man so genannte verallgemeinerte Kleinste-Quadrate-Ansätze. Wichtige Spezialfälle haben dann wieder eigene Namen, etwa die gewichteten kleinsten Quadrate (engl. weighted least squares (WLS)), bei denen die Fehler zwar weiter als unkorreliert angenommen werden, aber nicht mehr von gleicher Varianz. Dies führt auf ein Problem der Form

$\|D(A\alpha -y)\|_{2},$

wobei D eine Diagonalmatrix ist. Variieren die Varianzen stark, so haben die entsprechenden Normalgleichungen eine sehr große Kondition, weswegen das Problem direkt gelöst werden sollte.

Nimmt man noch weiter an, dass die Fehler in den Messdaten auch in der Modellfunktion berücksichtigt werden sollten, ergeben sich die „totalen kleinsten Quadrate“ in der Form

$\min _{E,r}\|(E,r)\|_{F},(A+E)\alpha =b+r,$

wobei der Fehler im Modell und der Fehler in den Daten ist.

Schließlich gibt es noch die Möglichkeit, keine Normalverteilung zugrunde zu legen. Dies entspricht beispielsweise der Minimierung nicht in der euklidischen Norm, sondern der Summennorm. Solche Modelle sind Thema der Regressionsanalyse.

Basierend auf einem Artikel in:

Wikipedia.de