Wahrscheinlichkeitsdichtefunktion

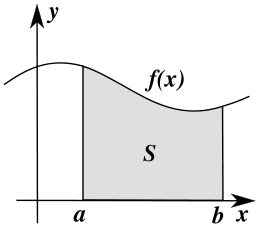
Die Wahrscheinlichkeit, dass eine Zufallsvariable einen Wert zwischen und annimmt, entspricht dem Inhalt der Fläche unter dem Graph der Wahrscheinlichkeitsdichtefunktion .

Eine Wahrscheinlichkeitsdichtefunktion, oft kurz Dichtefunktion, Wahrscheinlichkeitsdichte, Verteilungsdichte oder nur Dichte genannt und mit WDF oder englisch pdf von probability density function abgekürzt, ist eine spezielle reellwertige Funktion in der Stochastik, einem Teilgebiet der Mathematik. Dort dienen die Wahrscheinlichkeitsdichtefunktionen zur Konstruktion von Wahrscheinlichkeitsverteilungen mithilfe von Integralen sowie zur Untersuchung und Klassifikation von Wahrscheinlichkeitsverteilungen.

Im Gegensatz zu Wahrscheinlichkeiten können Wahrscheinlichkeitsdichtefunktionen auch Werte über eins annehmen. Die Konstruktion von Wahrscheinlichkeitsverteilungen über Wahrscheinlichkeitsdichtefunktionen beruht auf der Idee, dass die Fläche zwischen der Wahrscheinlichkeitsdichtefunktion und der x-Achse von einem Punkt bis zu einem Punkt der Wahrscheinlichkeit entspricht, einen Wert zwischen und zu erhalten. Nicht der Funktionswert der Wahrscheinlichkeitsdichtefunktion ist somit relevant, sondern die Fläche unter ihrem Funktionsgraph, also das Integral.

In einem allgemeineren Kontext handelt es sich bei Wahrscheinlichkeitsdichtefunktionen um Dichtefunktionen (im Sinne der Maßtheorie) bezüglich des Lebesgue-Maßes.

Während im diskreten Fall Wahrscheinlichkeiten von Ereignissen durch Aufsummieren der Wahrscheinlichkeiten der einzelnen Elementarereignisse berechnet werden können (ein idealer Würfel zeigt beispielsweise jede Zahl mit einer Wahrscheinlichkeit von $\tfrac 1 6$ ), gilt dies nicht mehr für den stetigen Fall. Beispielsweise sind zwei Menschen kaum exakt gleich groß, sondern nur bis auf Haaresbreite oder weniger. In solchen Fällen sind Wahrscheinlichkeitsdichtefunktionen nützlich. Mit Hilfe dieser Funktionen lässt sich die Wahrscheinlichkeit für ein beliebiges Intervall – beispielsweise eine Körpergröße zwischen 1,80 m und 1,81 m – bestimmen, obwohl unendlich viele Werte in diesem Intervall liegen, von denen jeder einzelne die Wahrscheinlichkeit $0$ hat.

Definition

Wahrscheinlichkeitsdichten können auf zwei Arten definiert werden: einmal als Funktion, aus der sich eine Wahrscheinlichkeitsverteilung konstruieren lässt, das andere Mal als Funktion, die aus einer Wahrscheinlichkeitsverteilung abgeleitet wird. Unterschied ist also die Richtung der Herangehensweise.

Zur Konstruktion von Wahrscheinlichkeitsmaßen

Gegeben sei eine reelle Funktion

$f\colon \mathbb {R} \to \mathbb {R}$ , für die gilt:

ist nichtnegativ, das heißt, $f(x)\geq 0$ für alle $x\in \mathbb {R}$ .
ist integrierbar.
ist normiert in dem Sinne, dass

$\int _{-\infty }^{\infty }f(x)\,\mathrm {d} x=1$ .

Dann heißt eine Wahrscheinlichkeitsdichtefunktion und definiert durch

$P([a,b]):=\int _{a}^{b}f(x)\,\mathrm {d} x$

eine Wahrscheinlichkeitsverteilung auf den reellen Zahlen.

Aus Wahrscheinlichkeitsmaßen abgeleitet

Gegeben sei eine Wahrscheinlichkeitsverteilung oder eine reellwertige Zufallsvariable .

Existiert eine reelle Funktion , sodass für alle $a\in \mathbb {R}$

$P((-\infty ,a])=\int _{-\infty }^{a}f(x)\,\mathrm {d} x$

bzw.

$P(X\leq a)=\int _{-\infty }^{a}f(x)\,\mathrm {d} x$

gilt, so heißt die Wahrscheinlichkeitsdichtefunktion von bzw. von .

Beispiele

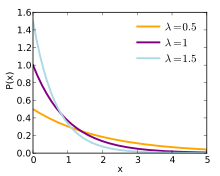
Wahrscheinlichkeitsdichtefunktionen der Exponentialverteilung für verschiedene Parameter.

Eine Wahrscheinlichkeitsverteilung, die über eine Wahrscheinlichkeitsdichtefunktion definiert werden kann, ist die Exponentialverteilung. Sie besitzt die Wahrscheinlichkeitsdichtefunktion

$f_{\lambda }(x)={\begin{cases}\displaystyle \lambda \mathrm {e} ^{-\lambda x}&x\geq 0\\0&x<0\end{cases}}$

Hierbei ist $\lambda >0$ ein reeller Parameter. Insbesondere überschreitet die Wahrscheinlichkeitsdichtefunktion für Parameter $\lambda >1$ an der Stelle x=0 den Funktionswert , wie in der Einleitung beschrieben. Dass es sich bei $f_{\lambda }(x)$ wirklich um eine Wahrscheinlichkeitsdichtefunktion handelt, folgt aus den elementaren Integrationsregeln für die Exponentialfunktion, Positivität und Integrierbarkeit der Exponentialfunktion sind klar.

Eine Wahrscheinlichkeitsverteilung, aus der eine Wahrscheinlichkeitsdichtefunktion abgeleitet werden kann, ist die stetige Gleichverteilung auf dem Intervall [0,1] . Sie ist definiert durch

$P([a,b])=b-a$ für $a\leq b$ und $a,b\in [0,1]$

Außerhalb des Intervalls erhalten alle Ereignisse die Wahrscheinlichkeit null. Gesucht ist nun eine Funktion , für die

$\int _{a}^{b}f(x)\,\mathrm {d} x=P([a,b])=b-a$

gilt, falls $a,b\in [0,1]$ . Die Funktion

$f(x)=1$

erfüllt dies. Sie wird dann außerhalb des Intervalles [0,1] durch die Null fortgesetzt, um problemlos über beliebige Teilmengen der reellen Zahlen integrieren zu können. Eine Wahrscheinlichkeitsdichtefunktion der stetigen Gleichverteilung wäre somit:

$f(x)={\begin{cases}\displaystyle 1&{\text{ falls }}x\in [0,1]\\0&{\text{ sonst }}\end{cases}}$

Ebenso wäre die Wahrscheinlichkeitsdichtefunktion

$f(x)={\begin{cases}\displaystyle 1&{\text{ falls }}x\in (0,1)\\0&{\text{ sonst }}\end{cases}}$

möglich, da sich beide nur auf einer Lebesgue-Nullmenge unterscheiden und beide den Anforderungen genügen. Man könnte beliebig viele Wahrscheinlichkeitsdichtefunktionen allein durch Abwandlung des Wertes an einem Punkt erzeugen. Faktisch ändert dies nichts an den Eigenschaft der Funktion, Wahrscheinlichkeitsdichtefunktion zu sein, da das Integral diese kleinen Modifikationen ignoriert.

Bemerkungen zur Definition

Streng genommen handelt es sich bei dem Integral in der Definition um ein Lebesgue-Integral bezüglich des Lebesgue-Maßes $\lambda$ und es müsste dementsprechend als $\mathrm {d} \lambda (x)$ geschrieben werden. In den meisten Fällen ist das herkömmliche Riemann-Integral aber ausreichend, weshalb hier $\mathrm {d} x$ geschrieben wird. Nachteil des Riemann-Integrals auf struktureller Ebene ist, dass es sich nicht wie das Lebesgue-Integral in einen allgemeinen maßtheoretischen Rahmen einbetten lässt. Für Details zur Beziehung von Lebesgue- und Riemann-Integral siehe Riemann- und Lebesgue-Integral.

Manche Autoren unterscheiden die beiden obigen Herangehensweisen auch namentlich. So wird die Funktion, die zur Konstruktion von Wahrscheinlichkeitsverteilungen verwendet wird, dann Wahrscheinlichkeitsdichte genannt, die aus einer Wahrscheinlichkeitsverteilung abgeleitete Funktion hingegen Verteilungsdichte.

Existenz und Eindeutigkeit

Konstruktion von Wahrscheinlichkeitsverteilungen

Das in der Definition beschriebene liefert wirklich eine Wahrscheinlichkeitsverteilung. Denn aus der Normiertheit folgt $P(\mathbb {R} )=1$ . Dass die Wahrscheinlichkeiten alle positiv sind, folgt aus der Positivität der Funktion. Die σ-Additivität folgt aus dem Satz von der majorisierten Konvergenz mit der Wahrscheinlichkeitsdichtefunktion als Majorante und der Funktionenfolge

$f_{n}:=\sum _{i=1}^{n}f\chi _{A_{i}}$ ,

mit paarweise disjunkten Mengen A_i .

Hierbei bezeichnet $\chi_A$ die charakteristische Funktion auf der Menge .

Dass die Wahrscheinlichkeitsverteilung eindeutig ist, folgt aus dem Maßeindeutigkeitssatz und der Schnittstabilität des Erzeugers der Borelschen σ-Algebra, hier das Mengensystem der abgeschlossenen Intervalle.

Aus einer Wahrscheinlichkeitsdichtefunktion abgeleitet

Die zentrale Aussage über die Existenz einer Wahrscheinlichkeitsdichtefunktion zu einer vorgegebenen Wahrscheinlichkeitsverteilung ist der Satz von Radon-Nikodým:

Die Wahrscheinlichkeitsverteilung besitzt genau dann eine Wahrscheinlichkeitsdichtefunktion, wenn sie absolut stetig bezüglich des Lebesgue-Maßes $\lambda$ ist. Das bedeutet, dass aus $\lambda (A)=0$ immer P(A)=0

folgen muss.

Es kann durchaus mehr als eine solche Wahrscheinlichkeitsdichtefunktion existieren, aber diese unterscheiden sich nur auf einer Menge vom Lebesgue-Maß 0 voneinander, sind also fast überall identisch.

Somit können diskrete Wahrscheinlichkeitsverteilungen keine Wahrscheinlichkeitsdichtefunktion besitzen, denn für sie gilt immer $P(\{k\})>0$ für ein passendes Element $k\in \mathbb {R}$ . Solche Punktmengen besitzen aber immer das Lebesgue-Maß 0, somit sind diskrete Wahrscheinlichkeitsverteilungen nicht absolut stetig bezüglich des Lebesgue-Maßes.

Berechnung von Wahrscheinlichkeiten

Grundlage

Die Wahrscheinlichkeit für ein Intervall lässt sich mit der Wahrscheinlichkeitsdichte berechnen als

$P(X\in [a,b])=\int _{a}^{b}f(x)\,\mathrm {d} x$ .

Diese Formel gilt ebenso für die Intervalle (a,b) , (a,b] und [a,b) , denn es liegt in der Natur stetiger Zufallsvariablen, dass die Wahrscheinlichkeit für das Annehmen eines konkreten Wertes $0$ ist (unmögliches Ereignis). Formal ausgedrückt gilt:

$\forall x\in \mathbb {R} \colon \,P(X=x)=0$

$P(a\leq X\leq b)=P(a<X\leq b)=P(a\leq X<b)=P(a<X<b)$

Für komplexere Mengen kann die Wahrscheinlichkeit analog durch Integrieren über Teilintervalle ermittelt werden. Allgemein erhält die Wahrscheinlichkeit die Form

$P(X\in A)=\int _{A}f(x)\,\mathrm {d} x$ .

Hilfreich ist oft die σ-Additivität der Wahrscheinlichkeitsverteilung. Das bedeutet: Sind $A_{1},A_{2},A_{3}\dotsc$ paarweise disjunkte Intervalle und ist

$A=\bigcup _{i=1}^{\infty }A_{i}$

die Vereinigung all dieser Intervalle, so gilt

$P(A)=P\left(\bigcup _{i=1}^{\infty }A_{i}\right)=\sum _{i=1}^{\infty }\int _{a_{i}}^{b_{i}}f(x)\,\mathrm {d} x$ .

Dabei sind die Intervalle von der Form $A_{i}=(a_{i},b_{i})$ . Dies gilt auch für endlich viele Intervalle. Ist somit die Wahrscheinlichkeit von disjunkten Intervallen zu berechnen, so kann man entsprechend zuerst die Wahrscheinlichkeit jedes einzelnen Intervalles berechnen und diese Wahrscheinlichkeiten dann aufsummieren.

Beispiel: Zeit zwischen Anrufen in einem Callcenter

Die Zeit zwischen zwei Anrufen in einem Callcenter ist erfahrungsgemäß ungefähr exponentialverteilt zu einem Parameter $\lambda$ und besitzt demnach die Wahrscheinlichkeitsdichtefunktion

$f_{\lambda }(x)={\begin{cases}\displaystyle \lambda \mathrm {e} ^{-\lambda x}&x\geq 0\\0&x<0\end{cases}}$ ,

vergleiche auch den Abschnitt Beispiele und den Artikel Poisson-Prozess. Dabei ist die x-Achse mit einer beliebigen Zeiteinheit versehen (Stunden, Minuten, Sekunden). Der Parameter $\lambda$ entspricht dann der mittleren Anzahl von Anrufen pro Zeiteinheit.

Die Wahrscheinlichkeit, dass der nächste Anruf ein bis zwei Zeiteinheiten nach dem vorangegangenen eintritt, ist dann

$P(X\in [1,2])=\int _{1}^{2}\lambda \mathrm {e} ^{-\lambda x}\,\mathrm {d} x=\lbrack -\mathrm {e} ^{-\lambda x}\rbrack _{1}^{2}=-\mathrm {e} ^{-2\lambda }+\mathrm {e} ^{-\lambda }$ .

Angenommen, eine Servicekraft im Callcenter benötigt fünf Zeiteinheiten für eine Pause. Die Wahrscheinlichkeit, dass sie keinen Anruf verpasst, ist gleich der Wahrscheinlichkeit, dass der nächste Anruf zum Zeitpunkt fünf oder später eingeht. Es ist damit

$P(X\geq 5)=1-P(X\leq 5)=1-\int _{0}^{5}\lambda \mathrm {e} ^{-\lambda x}\,\mathrm {d} x=1-\lbrack -\mathrm {e} ^{-\lambda x}\rbrack _{0}^{5}=1-(-\mathrm {e} ^{-5\lambda }+1)=\mathrm {e} ^{-5\lambda }$

Eigenschaften

Zusammenhang von Verteilungsfunktion und Dichtefunktion

Wahrscheinlichkeitsdichte der Lognormalverteilung (mit $\mu =0$ )

Kumulative Verteilungsfunktion der Lognormalverteilung (mit $\mu =0$ )

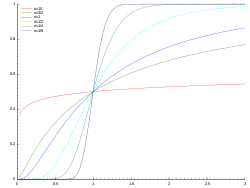
Die Verteilungsfunktion einer Zufallsvariablen oder einer Wahrscheinlichkeitsverteilung mit Wahrscheinlichkeitsdichtefunktion $f_{X}$ beziehungsweise f_P wird als Integral über die Dichtefunktion gebildet:

$F_{X}(x)=\int _{-\infty }^{x}f_{X}(t)\,\mathrm {d} t$

$F_{P}(x)=\int _{-\infty }^{x}f_{P}(t)\,\mathrm {d} t$

Dies folgt direkt aus der Definition der Verteilungsfunktion. Die Verteilungsfunktionen von Zufallsvariablen oder Wahrscheinlichkeitsverteilungen mit Wahrscheinlichkeitsdichtefunktion sind somit immer stetig.

Wenn die Verteilungsfunktion differenzierbar ist, ist ihre Ableitung eine Dichtefunktion der Verteilung:

$F^{\prime }(x)={\frac {\operatorname {d} F(x)}{\operatorname {d} x}}=f(x)$

Dieser Zusammenhang gilt auch dann noch, wenn stetig ist und es höchstens abzählbar viele Stellen $x\in \mathbb {R}$ gibt, an denen nicht differenzierbar ist; welche Werte man an diesen Stellen für f(x) verwendet, ist unerheblich.

Allgemein existiert eine Dichtefunktion genau dann, wenn die Verteilungsfunktion absolut stetig ist. Diese Bedingung impliziert unter anderem, dass stetig ist und fast überall eine Ableitung besitzt, die mit der Dichte übereinstimmt.

Es ist jedoch zu beachten, dass es Verteilungen wie die Cantor-Verteilung gibt, die eine stetige, fast überall differenzierbare Verteilungsfunktion besitzen, aber dennoch keine Wahrscheinlichkeitsdichte. Fast überall differenzierbar sind Verteilungsfunktionen immer, aber die entsprechende Ableitung erfasst generell nur den absolutstetigen Anteil der Verteilung.

Dichten auf Teilintervallen

Die Wahrscheinlichkeitsdichte einer Zufallsvariablen , die nur Werte in einem Teilintervall der reellen Zahlen annimmt, kann so gewählt werden, dass sie außerhalb des Intervalls den Wert $0$ hat. Ein Beispiel ist die Exponentialverteilung mit $I=[0,\infty[$ . Alternativ kann die Wahrscheinlichkeitsdichte als eine Funktion $f\colon I\to\R$ betrachtet werden, d.h. als eine Dichte der Verteilung auf bezüglich des Lebesgue-Maßes auf .

Nichtlineare Transformation

Im Falle der nichtlinearen Transformation Y=g(X) gilt

$\operatorname {E} (Y)=\operatorname {E} (g(X))=\int _{-\infty }^{\infty }g(x)f(x)\,\mathrm {d} x$ .

Faltung und Summe von Zufallsvariablen

Für Wahrscheinlichkeitsverteilungen mit Wahrscheinlichkeitsdichtefunktionen kann die Faltung (von Wahrscheinlichkeitsverteilungen) auf die Faltung (von Funktionen) der entsprechenden Wahrscheinlichkeitsdichtefunktionen zurückgeführt werden. Sind P,Q Wahrscheinlichkeitsverteilungen mit Wahrscheinlichkeitsdichtefunktionen f_P und $f_{Q}$ , so ist

$f_{P*Q}=f_{P}*f_{Q}$ .

Hierbei bezeichnet $P*Q$ die Faltung von und und $f*g$ die Faltung der Funktionen und . Die Wahrscheinlichkeitsdichtefunktion der Faltung zweier Wahrscheinlichkeitsverteilungen ist somit genau die Faltung der Wahrscheinlichkeitsdichtefunktionen der Wahrscheinlichkeitsverteilungen.

Diese Eigenschaft überträgt sich direkt auf die Summe von stochastisch unabhängigen Zufallsvariablen. Sind zwei stochastisch unabhängige Zufallsvariablen $X,Y$ mit Wahrscheinlichkeitsdichtefunktionen $f_{X}$ und $f_{Y}$ gegeben, so ist

$f_{X+Y}=f_{X}*f_{Y}$ .

Die Wahrscheinlichkeitsdichtefunktion der Summe ist somit die Faltung der Wahrscheinlichkeitsdichtefunktionen der einzelnen Zufallsvariablen.

Bestimmung von Kennzahlen durch Wahrscheinlichkeitsdichtefunktionen

Viele der typischen Kennzahlen einer Zufallsvariablen beziehungsweise einer Wahrscheinlichkeitsverteilung lassen sich bei Existenz der Wahrscheinlichkeitsdichtefunktionen direkt aus dieser herleiten.

Modus

Der Modus einer Wahrscheinlichkeitsverteilung bzw. Zufallsvariablen wird direkt über die Wahrscheinlichkeitsdichtefunktion definiert. Ein $x_{\text{mod}}\in \mathbb {R}$ heißt ein Modus, wenn die Wahrscheinlichkeitsdichtefunktion an der Stelle $x_{\text{mod}}$ ein lokales Maximum besitzt. Das bedeutet, es ist

$f(x)\leq f(x_{\text{mod}})$ für alle $x\in (x_{\text{mod}}-\varepsilon ;x_{\text{mod}}+\varepsilon )$

für ein $\varepsilon >0$ .

Selbstverständlich kann eine Wahrscheinlichkeitsdichtefunktion auch zwei oder mehrere lokale Maxima besitzen (bimodale Verteilungen und multimodale Verteilungen). Im Falle der Gleichverteilung im obigen Beispielabschnitt besitzt die Wahrscheinlichkeitsdichtefunktion sogar unendlich viele lokale Maxima.

Median

Der Median wird gewöhnlicherweise über die Verteilungsfunktion oder spezieller über die Quantilfunktion definiert. Existiert eine Wahrscheinlichkeitsdichtefunktion, so ist ein Median gegeben durch dasjenige $x_{\text{med}}$ , für das

$\int _{-\infty }^{x_{\text{med}}}f(x)\,\mathrm {d} x={\frac {1}{2}}$

und

$\int _{x_{\text{med}}}^{+\infty }f(x)\,\mathrm {d} x={\frac {1}{2}}$

gilt. Aufgrund der Stetigkeit der zugehörigen Verteilungsfunktion existiert in diesem Fall $x_{\text{med}}$ immer, ist aber im Allgemeinen nicht eindeutig.

Erwartungswert

Der Erwartungswert einer Zufallsvariablen mit Wahrscheinlichkeitsdichtefunktion $f_{X}$ ist gegeben durch

$\operatorname {E} (X)=\int _{-\infty }^{+\infty }xf(x)\,\mathrm {d} x$ ,

falls das Integral existiert.

Varianz und Standardabweichung

Ist eine Zufallsvariable mit Wahrscheinlichkeitsdichtefunktion $f_{X}$ gegeben, und bezeichnet

$\mu =\operatorname {E} (X)$

den Erwartungswert der Zufallsvariablen, so ist die Varianz der Zufallsvariablen gegeben durch

$\operatorname {Var} (X)=\operatorname {E} \left((X-\mu )^{2}\right)=\int _{-\infty }^{+\infty }(x-\mu )^{2}f_{X}(x)\,\mathrm {d} x$ .

Alternativ gilt auch nach dem Verschiebungssatz

$\operatorname {Var} (X)=\operatorname {E} (X^{2})-(\operatorname {E} (X))^{2}=\int _{-\infty }^{\infty }x^{2}f_{X}(x)\,\mathrm {d} x-\mu ^{2}$ .

Auch hier gelten die Aussagen wieder nur, wenn alle vorkommenden Integrale existieren. Die Standardabweichung lässt sich dann direkt als die Wurzel aus der Varianz berechnen.

Höhere Momente, Schiefe und Wölbung

Mittels der oben angegebenen Vorschrift für nichtlineare Transformationen lassen sich auch höhere Momente direkt berechnen. So gilt für das k-te Moment einer Zufallsvariablen mit Wahrscheinlichkeitsdichtefunktion $f_{X}$

$m_{k}=\int _{-\infty }^{+\infty }x^{k}f_{X}(x)\,\mathrm {d} x$

und für das k-te absolute Moment

$M_{k}=\int _{-\infty }^{+\infty }|x|^{k}f_{X}(x)\,\mathrm {d} x$ .

Bezeichnet $\mu$ den Erwartungswert von , so ergibt sich für die zentralen Momente

$\mu _{k}=\int _{-\infty }^{+\infty }(x-\mu )^{k}f_{X}(x)\,\mathrm {d} x$

und die absoluten zentralen Momente

${\overline {\mu }}_{k}=\int _{-\infty }^{+\infty }|x-\mu |^{k}f_{X}(x)\,\mathrm {d} x$ .

Über die zentralen Momente können die Schiefe und die Wölbung der Verteilung direkt bestimmt werden, siehe die entsprechenden Hauptartikel.

Beispiel

Gegeben sei wieder die Wahrscheinlichkeitsdichtefunktion der Exponentialverteilung zum Parameter $\lambda >0$ , also

$f_{\lambda }(x)={\begin{cases}\displaystyle \lambda \mathrm {e} ^{-\lambda x}&x\geq 0\\0&x<0\end{cases}}$

Ein Modus des Exponentialverteilung ist immer $x_{\text{mod}}=0$ . Denn auf dem Intervall $(-\infty ,0)$ ist die Wahrscheinlichkeitsdichtefunktion konstant gleich null, und auf dem Intervall $[0,+\infty )$ ist sie streng monoton fallend, somit ist an der Stelle 0 ein lokales Maximum. Aus der Monotonie folgt dann auch direkt, dass es sich um das einzige lokale Maximum handelt, der Modus ist also eindeutig bestimmt.

Zur Bestimmung des Medians bildet man (da die Wahrscheinlichkeitsdichtefunktion links der Null verschwindet)

$\int _{0}^{c}\lambda \mathrm {e} ^{-\lambda x}\,\mathrm {d} x=\lbrack -\mathrm {e} ^{-\lambda x}\rbrack _{0}^{c}=-\mathrm {e} ^{-\lambda c}+1\;{\stackrel {!}{=}}\;{\frac {1}{2}}$ .

Durch kurze Rechnung erhält man

$c={\frac {\ln 2}{\lambda }}$ .

Dieses erfüllt auch die zweite der beiden Gleichungen im obigen Abschnitt Median und ist somit ein Median.

Für den Erwartungswert erhält man unter Zuhilfenahme der partiellen Integration

$\operatorname {E} (X)=\int _{0}^{+\infty }x\lambda \mathrm {e} ^{-\lambda x}\,\mathrm {d} x=\lbrack -xe^{-\lambda x}\rbrack _{0}^{+\infty }-\int _{0}^{+\infty }-e^{-\lambda x}\,\mathrm {d} x=\lbrack {\tfrac {1}{-\lambda }}e^{-\lambda x}\rbrack _{0}^{+\infty }={\frac {1}{\lambda }}$ .

Analog lässt sich durch zweimaliges Anwenden der partiellen Integration die Varianz bestimmen.

Weitere Beispiele

Durch f(x) = 3x^2 für $x \in [0,1]$ sowie f(x)=0 für x<0 und f(x)=0 für x>1 ist eine Dichtefunktion $f\colon \mathbb {R} \to \mathbb {R}$ gegeben, denn ist auf ganz $\mathbb {R}$ nichtnegativ und es gilt

$\int_{-\infty}^{\infty} f(x) \, \mathrm dx = \int_0^1 3x^2 \, \mathrm dx = 1$ .

Für $x \in [0,1]$ gilt:

$F(x) = \int_{-\infty}^{x} f(t) \, \mathrm dt = \int_0^x 3t^2 \, \mathrm dt = x^3$

Die Verteilungsfunktion lässt sich schreiben als

$F_{X}(x)={\begin{cases}0&{\text{ falls }}x<0\\x^{3}&{\text{ falls }}0\leq x\leq 1\\1&{\text{ falls }}x>1\end{cases}}$

Ist eine Zufallsvariable mit der Dichte , so folgt daher beispielsweise

$P(X \leq \tfrac{1}{2}) = F(\tfrac{1}{2}) = \tfrac{1}{8}$ .

Für den Erwartungswert von ergibt sich

$\operatorname {E} (X)=\int _{-\infty }^{\infty }xf(x)\,\mathrm {d} x=\int _{0}^{1}3x^{3}\,\mathrm {d} x={\frac {3}{4}}$ .

Mehrdimensionale Zufallsvariablen

Wahrscheinlichkeitsdichten kann man auch für mehrdimensionale Zufallsvariablen, also für Zufallsvektoren definieren. Ist eine $\mathbb {R} ^{n}$ -wertige Zufallsvariable, so heißt eine Funktion $f\colon \mathbb {R} ^{n}\to [0,\infty )$ Wahrscheinlichkeitsdichte (bezüglich des Lebesgue-Maßes) der Zufallsvariablen , falls gilt

$P(X\in A)=\int _{A}f(x)\,\mathrm {d} ^{n}x$

für alle Borelmengen $A\in\mathcal{B}(\R^n)$ .

Speziell folgt dann für -dimensionale Intervalle $I = [a_1,b_1] \times \dotsb \times [a_n,b_n]$ mit reellen Zahlen $a_1<b_1,\dotsc,a_n<b_n$ :

$P(X\in I)=\int _{a_{n}}^{b_{n}}\dotsi \int _{a_{1}}^{b_{1}}f(x_{1},\dotsc ,x_{n})\ \mathrm {d} x_{1}\dotso \mathrm {d} x_{n}$ .

Der Begriff der Verteilungsfunktion lässt sich ebenfalls auf mehrdimensionale Zufallsvariablen erweitern. Hier ist in der Notation $F(x)=P(X\leq x)$ das ein Vektor und das $\leq\,$ -Zeichen komponentenweise zu lesen. ist also hierbei eine Abbildung von $\mathbb {R} ^{n}$ in das Intervall [0,1] und es gilt

$F(x_{1},\dotsc ,x_{n})=\int _{-\infty }^{x_{n}}\dotsi \int _{-\infty }^{x_{1}}f(t_{1},\dotsc ,t_{n})\ \mathrm {d} t_{1}\dotso \mathrm {d} t_{n}$ .

Wenn n-mal stetig differenzierbar ist, erhält man eine Wahrscheinlichkeitsdichte durch partielle Differentiation:

$f(x_{1},x_{2},\dotsc ,x_{n})={\frac {\partial ^{n}F(x_{1},x_{2},\dotsc ,x_{n})}{\partial x_{1}\dotso \partial x_{n}}}.$

Die Dichten $f_{i}$ der Komponentenvariablen $X_{i}$ lassen sich als Dichten der Randverteilungen durch Integration über die übrigen Variablen berechnen.

Des Weiteren gilt: Ist $X=(X_{1},\dotsc X_{n})$ eine $\mathbb {R} ^{n}$ -wertige Zufallsvariable mit Dichte, so sind äquivalent:

besitzt eine Dichte der Form $f(x_{1},\dotsc ,x_{n})=f_{1}(x_{1})\cdot \ldots \cdot f_{n}(x_{n})$ , wobei $f_{i}$ die reelle Wahrscheinlichkeitsdichte von $X_{i}$ ist.

Die Zufallsvariablen $X_1, \dotsc, X_n$ sind unabhängig.

Schätzung einer Wahrscheinlichkeitsdichte anhand diskreter Daten

Häufigkeitsdichte

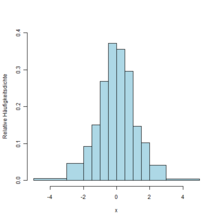
Diskret erfasste, aber eigentlich stetige Daten (beispielsweise die Körpergröße in Zentimetern) können als Häufigkeitsdichte repräsentiert werden. Das so erhaltene Histogramm ist eine stückweise konstante Schätzung der Dichtefunktion. Alternativ kann beispielsweise mit sogenannten Kerndichteschätzern die Dichtefunktion durch eine stetige Funktion geschätzt werden. Der dazu verwendete Kern sollte dem erwarteten Messfehler entsprechen.

Basierend auf einem Artikel in:

Wikipedia.de