Tensoralgebra

Die Tensoralgebra ist ein mathematischer Begriff, der in vielen Bereichen der Mathematik wie der linearen Algebra, der Algebra, der Differentialgeometrie sowie in der Physik verwendet wird. Sie fasst "alle Tensoren" über einem Vektorraum in der Struktur einer graduierten Algebra zusammen.

Definition

Es sei ein Vektorraum über einem Körper oder allgemeiner ein Modul über einem kommutativen Ring mit Einselement. Dann ist die Tensoralgebra (als Menge) definiert durch die direkte Summe aller Tensorprodukte des Raums mit sich selber.

$\mathrm {T} V=\bigoplus _{n\geq 0}V^{\otimes n}=K\oplus V\oplus (V\otimes V)\oplus (V\otimes V\otimes V)\oplus \ldots$

Mit der Multiplikation, die auf den homogenen Bestandteilen durch das Tensorprodukt gegeben ist, wird $\mathrm {T} V$ zu einer $\mathbb {N}$ -graduierten, unitären, assoziativen Algebra.

Universelle Eigenschaft

Ist eine assoziative - Algebra mit einem Einselement , sowie $f:V\to A$ eine lineare Abbildung, so existiert genau ein Algebrenhomomorphismus ${\tilde {f}}:TV\to A$ , so dass das Diagramm

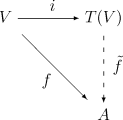
kommutiert. Dieser Algebrenhomomorphismus ist gegeben durch ${\tilde {f}}(v_{1}\otimes \dots \otimes v_{r})=f(v_{1})\dots f(v_{r})$ sowie ${\tilde {f}}(\lambda )=\lambda e$ .

Diese universelle Eigenschaft zeigt, dass ein Funktor von der Kategorie der K-Vektorräume in die Kategorie der K-Algebren ist. Der Funktor bildet

$f:V\to A$

auf

$T(f)={\tilde {f}}:T(V)\to A$

ab.

Beispiel

Ist ein -dimensionaler -Vektorraum (bzw. ein freier Modul vom Rang ), so ist $\mathrm {T} V$ isomorph zur freien assoziativen Algebra über in Unbestimmten.

Quotientenräume der Tensoralgebra

Durch Herausteilen eines bestimmten Ideals kann man aus der Tensoralgebra beispielsweise die symmetrische Algebra, die Äußere Algebra oder die Clifford-Algebra gewinnen. Diese Algebren sind in der Differentialgeometrie von Bedeutung.

Basierend auf einem Artikel in:

Wikipedia.de