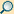Mohrscher Spannungskreis

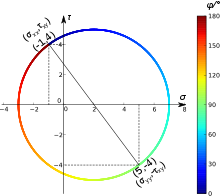
Der Mohrsche Kreis oder auch Mohrsche Spannungskreis, benannt nach Christian Otto Mohr, ist eine Möglichkeit, den 3D-Spannungszustand eines Punktes, oder eines Volumens konstanter Spannung, zu veranschaulichen oder zu untersuchen.
Dazu wird auf einem infinitesimalen
Volumen ein Freischnitt durchgeführt, wodurch der Traktionsvektor
t auf der Schnittfläche sichtbar wird. Dieser Traktionsvektor, auch
Spannungsvektor genannt, wird zerlegt in seinen Anteil
(hier auch
bezeichnet) senkrecht zur Schnittfläche (den sogenannten Normalspannungsanteil)
und seinen Anteil
(hier auch
bezeichnet) parallel zur Schnittfläche (den so genannte Schubspannungsanteil).
Abhängig vom Winkel
,
unter dem geschnitten wird, lassen sich Paare
berechnen und in ein Diagramm als Punkte einzeichnen. Die Menge aller Punkte ist
der Mohrsche Kreis. An ihm lassen sich z.B. die Hauptspannungen, die
Hauptspannungsrichtungen oder die größte Schubspannung ablesen. Dadurch gewinnt
man eine anschauliche Vorstellung von der Beanspruchung des Volumens. Bei
Festigkeitskriterien, wie Versagenskriterien,
Fließkriterien
oder Elastizitätsgrenzen, von isotropen,
homogenen
Materialien sind ausschließlich die Hauptspannungen relevant.
Bei einigen Festigkeitskriterien ist nur die Beanspruchung in der Ebene der
größten und kleinsten Hauptspannung relevant. Zu ihrer Beurteilung wird auch im
Computerzeitalter oft der Mohrsche Spannungskreis verwendet, denn er liefert
schnell eine anschauliche Lösung.
Der Mohrsche Kreis kann auch zur Berechnung des Traktionsvektors auf
eine beliebige Flächennormale verwendet werden und somit kann man die
Komponenten des Spannungstensors rückbestimmen: Sind die
Spannungstensor-Komponenten bezogen auf ein kartesisches -Koordinatensystem
gegeben, dann lassen sich mit dem Mohrschen Kreis die
Spannungstensor-Komponenten bezogen auf ein kartesisches
-Koordinatensystem
grafisch bestimmen. Vorausgesetzt ist hierbei, dass das
-Koordinatensystem
durch eine Drehung um den Winkel
aus dem
-Koordinatensystem
hervorgeht.
Neben dem Cauchy-Spannungstensor können auch andere symmetrische Tensoren mit dem Mohrschen Kreis veranschaulicht oder untersucht werden, z.B. der Verzerrungstensor. Und neben dem Mohrschen Kreis gibt es auch andere Verfahren zur Veranschaulichung symmetrischer Tensoren, z.B. Superquadriken oder Ellipsoide.
Schnittspannungsvektor
(x, y)-Komponenten
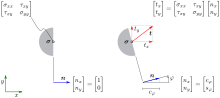
Der Spannungszustand an einem Teilchen ist festgelegt durch den symmetrischen
Cauchy-Spannungstensor
,
der meist als (2,0)-Tensor definiert wird. An diesem Teilchen und durch seine
unmittelbare Umgebung lässt sich ein Freischnitt führen in beliebiger Richtung.
An der entstandenen Schnittfläche lässt sich der Schnittspannungsvektor
t (traction vector) berechnen. Der Zusammenhang zwischen dem
Spannungstensor und dem Schnittspannungsvektor t ist
wobei n ein Normalen-Einheitsvektor ist, der senkrecht auf der
Schnittfläche steht und „nach außen“ zeigt. Die Komponenten des Spannungsvektors
t bezogen auf das kartesische -Koordinatensystem
werden aus den Komponenten des Spannungstensors und denen des
Normalen-Einheitsvektors mittels Matrixmultiplikation
bzw. nach der Summenkonvention
berechnet als:
Wenn an einem Schnittufer n der Normalen-Einheitsvektor ist, ist am gegenüber liegenden Schnittufer −n der Normalen-Einheitsvektor. Damit ist das Reaktionsprinzip mit der Definition des Spannungstensors von vornherein erfüllt.
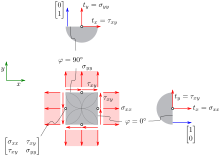
Die Komponenten von t bezogen auf das -Koordinatensystem
lassen sich für jede beliebige Schnittrichtung berechnen:
mit den Abkürzungen:
Besonders einfach ist die Berechnung für Schnitte parallel zu den Koordinatenflächen.
Bei
ist wegen
:
Bei
ist wegen
:
| Schnittwinkel |
||||
|---|---|---|---|---|
Die Komponenten des Spannungstensors sind also auch die Komponenten der Spannungen auf den Schnittflächen. Und der Mohrsche Kreis beschreibt, wie diese Spannungen von der Schnittrichtung abhängen.
(x̅, y̅)-Komponenten
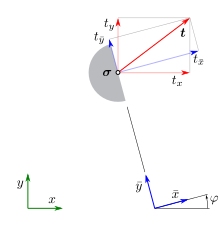
Im Abschnitt (x,
y)-Komponenten wurden die Komponenten von t bezogen auf das -Koordinatensystem
angegeben. Die Komponenten von t bezogen auf das
-Koordinatensystem
sind:
Durch Einsetzen und mit Hilfe der Umformungen
erhält man:
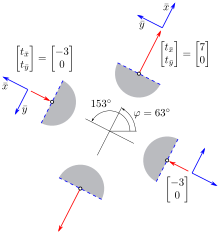
Auf diesen beiden Gleichungen basiert die Konstruktion des Mohrschen Kreises. Für das Beispiel:
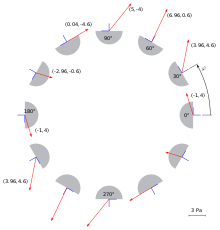
sind diese Formeln im Bild 5 für 12 verschiedene Winkel ausgewertet.
Bild 5 zeigt nicht den Mohrschen Kreis. Sondern Bild 5
veranschaulicht die Formeln für
und
.
Man sieht an jedem Schnitt den dort wirkenden Schnittspannungsvektor und seine
-Komponenten –
also seine Komponenten in Bezug auf das
-Koordinatensystem.
Den Mohrschen Kreis erhält man, indem man
über
aufträgt – indem man also ein Diagramm zeichnet, worin die Paare
als Punkte dargestellt sind. Dies wird im folgenden Abschnitt getan.
Für Schnitte parallel zu den -Koordinatenflächen
ist:
| Schnittwinkel |
||||
|---|---|---|---|---|
Kreisgleichung und Hauptspannungen
Kreisgleichung
Aus den Gleichungen für
und
wird die Kreisgleichung
des Mohrschen Kreises abgeleitet. Quadrieren beider Gleichungen liefert
zunächst:
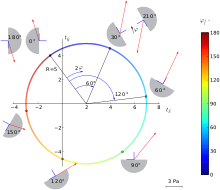
Und durch Addieren dieser Gleichungen erhält man die Gleichung eines Kreises mit Radius R und Mittelpunkt bei (a,b), nämlich:
Der Mittelpunkt des Mohrschen Kreises liegt bei:
Für das Beispiel ergibt sich (vgl. Bild 6):
Und der Radius beträgt:
Für das Beispiel ergibt sich (vgl. Bild 6):
Hauptspannungen und Hauptspannungsrichtungen
Die Hauptspannungen sind die Eigenwerte (der Komponentenmatrix) des Spannungstensors. Die charakteristische Gleichung zur Berechnung der Eigenwerte ist:
Einfache Umformungen
| Umformungen |
|---|
|
|
führen auf:
sodass man die Hauptspannungen als Schnittpunkte des Kreises mit der -Achse
abliest. Für das konkrete Beispiel ergeben sich die Hauptspannungen:
Es gibt verschiedene Methoden, um die Hauptspannungsrichtungen zu bestimmen.
Berechnung aus Kreisgleichung
Im Spezialfall
ist t parallel zum Normalen-Einheitsvektor n.
Aus der Kreisgleichung folgt dann:
Und für das Beispiel ergeben sich die positiven Schnittwinkel:
Berechnung aus Eigenvektoren
Die Richtungen lassen sich alternativ mit den Eigenvektoren bestimmen. Der zu
gehörende Eigenvektor
ist Lösung von:
Die Hauptspannungsrichtung für
ergibt sich entsprechend zu:
Nun liegen die (x,y)-Komponenten beider Eigenvektoren fest. Der Winkel zwischen x-Achse und erstem Eigenvektor ist damit:
Die zweite Eigenrichtung ist um 90 Grad gegenüber der ersten gedreht, sodass:
Die Einheitsvektoren der Eigenvektoren bilden eine Orthonormalbasis, die
den physikalischen Raum aufspannen, diese Eigenvektoren werden mit
bezeichnet. Da der Spannungstensor
mit den Einheitseigenvektoren multipliziert (
)
jeweils eine der Hauptspannungen ergeben, werden sie in diesem Zusammenhang auch
bezeichnet.
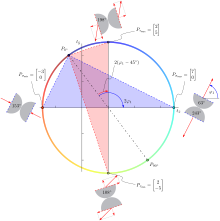
Mohrsche Spannungskreise in 3D
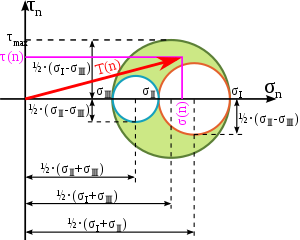
Die dreidimensionale Realität kann man mit 3 Mohrschen Spannungskreisen darstellen. Es gibt einen äußeren, der die Ebene von σⅢ und σI aufspannt. Jeder Traktionsvektor muss innerhalb des äußeren Kreises (oder auf dem äußeren Kreis) liegen. Jene Spannungskombinationen aus Normalspannung und Schubspannung, die innerhalb der inneren Kreise liegt, können nicht auftreten, woraus auch folgt, dass es ausschließlich 3 Normalspannungen gibt, bei denen die Schubspannung null ist. Bei einem Spannungszustand, bei dem zwei Hauptspannungen null sind, degeneriert ein Kreis zu einem Punkt und der andere innere Kreis ist ident mit dem äußeren Kreis. Bei einem hydrostatischen Spannungszustand degenerieren alle drei Kreise zu einem Punkt, da hier keine Schubspannungen vorhanden sind und in jeder Richtung dieselbe Normalspannung vorliegt.
Bestimmung des Normalenvektors bzw. des Traktionsvektors
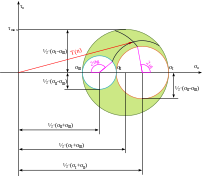
Man zeichnet die drei Spannungskreise und jenen Spannungspunkt (den Punkt, auf den der Traktionsvektor T(n) hinweisen soll) ein, der gesucht ist. Dieser Punkt muss sich zwischen den drei Kreisen befinden, liegt er exakt auf einem Kreis kann der Normalenvektor wie bei dem 2D-Spannungskreis ermittelt werden. Ein Spannungspunkt außerhalb des äußeren oder innerhalb eines der kleineren Kreise kann nicht angenommen werden. Durch Einstechen in einem der drei Mittelpunkte der Spannungskreise und Abtragen des Abstandes auf einem der beiden Kreise mit einem anderen Mittelpunkt, kann man wie in 2D den doppelten Winkel zu einer Hauptspannungsrichtung bestimmen. Damit kann man den Normalenvektor bestimmen:
Dabei reicht es aus, zwei Winkel zu bestimmen und den dritten über n²=cos²(αI)+cos²(αⅡ)+cos²(αⅢ) zu bestimmen. Ebenso ist eine grafische Bestimmung des Traktionsvektors für einen bestimmten Normalenvektor möglich, hier muss man die zuvor erwähnten Schritte in umgekehrter Reihenfolge durchführen.
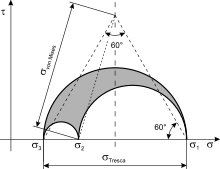
Durch die Hauptnormalspannungen σI und σIII wird eine Seite eines gleichseitigen Dreiecks aufgespannt. Der Abstand zwischen dem Punkt des soeben aufgespannten Dreiecks, der nicht auf der Abszisse liegt, und σII entspricht der von-Mises-Vergleichsspannung.
Mohrscher Kreis: Konstruktion und Auswertung
Konstruktion
Die Konstruktion des Mohrschen Kreises geschieht wie in nebenstehenden Bild dargestellt nach folgendem Schema:
- Zeichnen eines kart. Koordinatensystems für Punkte
.
- Eintragen der zwei Punkte:
.
- Verbinden dieser zwei Punkte durch eine Gerade (strich-punktierte Linie).
- Zeichnen des Kreises, der die Punkte
und
beinhaltet und dessen Mittelpunkt der Schnittpunkt der strichpunktierten Linie mit der
-Achse ist.
- Eintragen/Ablesen der zwei Punkte:
- Verbinden dieser zwei Punkte mit
(blaue gestrichelte Linien).
- Eintragen/Ablesen der zwei Punkte:
- Verbinden dieser zwei Punkte mit
(rote gestrichelte Linien).
Auswertung
- 1. Schnittrichtung / Schnittspannung
- Jeder Punkt auf dem Mohrschen Kreis im Bild im
Absatz Konstruktion entspricht einem Schnittwinkel
, siehe Bild 5.
ist einerseits der Winkel zwischen der x-Achse und dem Normalen-Einheitsvektor n – ausgehend von x entgegen dem Uhrzeigersinn positiv gezählt (in Bild 5). Andererseits ist
im Mohrschen Kreis, bzw. dem Bild im Absatz Konstruktion, der Winkel zwischen
und dem zur jeweiligen Schnittrichtung passenden Punkt
– von
ausgehend im Uhrzeigersinn positiv gezählt.
- Für jeden vorgegebenen Schnittwinkel
liest man im Mohrschen Kreis die
-Komponenten des zu dieser Schnittrichtung passenden Schnittspannungsvektors ab. Diese Komponenten sind das Paar
, das abzulesen ist an der Stelle
.
- 2. Hauptspannungen
- An den Schnittpunkten des Kreises mit der
-Achse sind die
-Komponenten der Spannungsvektoren
bzw.
. Der Schnittspannungsvektor t ist an diesen Schnittpunkten also parallel zu n, und darum sind
bzw.
die Hauptspannungen.
- 3. Hauptspannungsrichtungen
- Die zwei zugehörigen Hauptspannungsrichtungen stehen senkrecht
aufeinander. Darum reicht es aus, die zu
gehörende Richtung abzulesen. Diese ist gegeben durch den Schnittwinkel
, d.h. die Hälfte des Winkels
bzw. die blaue gestrichelte Linie zwischen
und
. Diese Linie/Richtung ist die Hauptspannungsrichtung. Die Richtung, unter der der Freischnitt ausgeführt wird, steht senkrecht dazu. Sie ist durch die blaue gestrichelte Linie zwischen
und
gegeben.
- 4. Extremwerte der Schubspannung
- Der Radius des Kreises ist die größte auftretende Schubspannung,
d.h.:
- Die zugehörigen Schnittwinkel sind um
versetzt zu den Schnittwinkeln, unter denen die Hauptspannungen auftreten (siehe rote gestrichelte Linien im Bild im Absatz Konstruktion).
Spezialfall: Wenn der Deviator-Anteil des Spannungstensors Null ist – d.h., wenn der Spannungstensor ein Kugeltensor ist – entartet der Kreis zu einem Punkt. Für die Komponenten des Spannungstensors gilt dann in jedem Koordinatensystem:
Verwandte Themen
Mohrsche Verzerrungskreise
Analog zu den Mohrschen Spannungskreisen kann man Mohrsche Verzerrungskreise zeichnen, die einem aufzeigen, welche Verzerrungszustände angenommen werden. Jedoch gibt es hier keinen Traktionsvektor, der die Spannungskomponenten auf eine beliebige Fläche angibt, wie bei den Spannungskreisen.
Tensorkomponenten aus zwei Schnitten

Seien die Spannungstensor-Komponenten bezüglich -Koordinatensystem
gegeben. Sei genau ein
-Koordinatensystem
definiert, das um einen Winkel
gegenüber dem
-Koordinatensystem
gedreht ist, siehe nebenstehendes Bild. Seien weiterhin die
Spannungstensors-Komponenten bezogen auf dieses eine
-Koordinatensystem
gesucht.
Dann lassen sich diese Komponenten bestimmen durch einen Schnitt unter –
und einen zweiten Schnitt unter
,
denn:
Die letzten Formeln ermöglichen es, die Komponenten des Spannungstensors in
Bezug auf ein um einen Winkel
gedrehtes Koordinatensystem zu berechnen. Die Funktionen
und
,
die dazu verwendet werden, sind dieselben wie die zur Konstruktion des Mohrschen
Kreises. Und darum kann man die Komponenten des Spannungstensors in Bezug auf
ein gedrehtes Koordinatensystem auch aus dem Mohrschen Kreis ablesen, siehe
hierzu das Bild am Beginn dieses Absatzes.
Tensorkomponenten aus Transformationsbeziehung
Diese -Komponenten
des Spannungstensors lassen sich auch direkt aus den
-Komponenten
des Spannungstensors berechnen. Denn der Koordinatenwechsel von
auf
erzeugt folgende Transformationsbeziehung (auch Pushforward genannt) für
die Komponenten des (2,0)-Spannungstensors:
Vergleich mit den Gleichungen für
und
liefert:
Dieses Ergebnis ist äquivalent zum Ergebnis aus dem letzten Abschnitt, siehe hierzu auch das Bild im Absatz Tensorkomponenten aus zwei Schnitten.
Häufig wird dieses Ergebnis auch geschrieben als:
Umrechnung Flächenträgheitsmomente

Die Transformationsregel für Flächenträgheitsmomente kann genau wie die Transformationsregel für die Komponenten des Spannungstensors bestimmt werden. Der Spannungstensor ist eine lineare Abbildung zwischen Vektoren gemäß:
Damit diese Abbildungen unabhängig von der Wahl des Koordinatensystems gelten, müssen die Komponenten des Spannungstensors folgenden Transformationsregeln erfüllen:
Völlig analog gilt bei einem Profilstab zwischen Biegemomenten
und Verkrümmungen
(bezogen auf die Neutralachse) mit den Flächenträgheitsmomenten definiert als
der lineare Zusammenhang:
Die Momente und die Verkrümmungen transformieren sich wie Pseudovektoren – also bei Drehung des Koordinatensystems wie Vektoren. Und darum ist die Transformationsregel für die Flächenträgheitsmomente:
Der Mohrsche Kreis kann also zur Umrechnung der Flächenträgheitsmomente bei Koordinatenwechsel ebenso verwendet werden wie zur Umrechnung der Komponenten des Spannungstensors.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 07.11. 2020