Langevin-Funktion

Langevin-Funktion

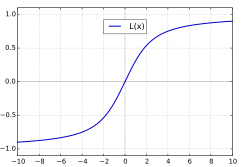
Die Langevin-Funktion $L(x)$ (nach dem Physiker Paul Langevin (1872–1946)) ist eine mathematische Funktion, die zur Berechnung von Orientierungspolarisation, Polarisation, Magnetisierung und Widerstand verwendet wird.

Definition

Die Langevin-Funktion^[1] ist definiert durch

$L(x)=\coth(x)-{1 \over x}$ ,

wobei $\coth$ den Kotangens hyperbolicus bezeichnet.

Eine Anwendung

Die bekannteste Anwendung ist die halbklassische Beschreibung eines Paramagneten in einem äußeren Magnetfeld. Dazu wird der Langevin-Parameter $\xi$ eingeführt:

$\xi ={\frac {mB}{k_{\mathrm {B} }T}}$

Die einzelnen Formelzeichen stehen für folgende Größen:

$m$ : Magnetisches Moment eines Teilchens
$B$ : Betrag der magnetischen Flussdichte des angelegten äußeren Magnetfeldes
$k_{\mathrm {B} }$ : Boltzmann-Konstante
$T$ : Absolute Temperatur

Für die Magnetisierung $M$ eines Paramagneten ergibt sich dann:

$M=NmL(\xi )$

$N$ steht dabei für die Stoffmenge und $m$ für das magnetische Moment der einzelnen Spins des Paramagneten. Eine weitere, quantenmechanische Beschreibung des Paramagnetismus ist durch die Brillouin-Funktion gegeben.

Reihenentwicklungen

Für alle reellen Werte x konvergent ist diese Summenreihe:

$L(x)=\sum _{n=1}^{\infty }{\frac {2x}{\pi ^{2}n^{2}+x^{2}}}$

Beispielsweise gilt für die diskrete Cauchy-Verteilung jene Summenreihe:

$\sum _{n=1}^{\infty }{\frac {1}{n^{2}+1}}={\frac {\pi L(\pi )}{2}}$

Somit ist die unendliche Summe der Kehrwerte von den Nachfolgern der Quadratzahlen elementar.

Und folgender Grenzwert gilt:

$\zeta (2)=\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}=\lim _{x\rightarrow 0}\sum _{n=1}^{\infty }{\frac {1}{n^{2}+x^{2}}}=\lim _{x\rightarrow 0}{\frac {\pi L(\pi x)}{2x}}={\frac {\pi ^{2}}{6}}$

Dieser Wert ist beim sogenannten Basler Problem die Lösung.

Die Maclaurinsche Reihe lautet wie folgt:

$L(x)=\sum _{n=1}^{\infty }2(-1)^{n+1}\pi ^{-2n}\zeta (2n)x^{2n-1}={\frac {1}{3}}x-{\frac {1}{45}}x^{3}+{\frac {2}{945}}x^{5}-{\frac {1}{4725}}x^{7}+\cdots$

Der Konvergenzradius dieser Reihe ist die Kreiszahl π.

Und für das Quadrat der Langevin-Funktion gilt:

$L(x)^{2}=\sum _{n=1}^{\infty }(4n+6)(-1)^{n+1}\pi ^{-2n-2}\zeta (2n+2)x^{2n}={\frac {1}{9}}x^{2}-{\frac {2}{135}}x^{4}+{\frac {1}{525}}x^{6}-{\frac {2}{8505}}x^{8}+\cdots$

Der griechische Buchstabe Zeta stellt die Riemannsche Zetafunktion dar.

Eine Näherung^[1] der Langevin-Funktion für $|x|\ll 1$ ist

$L(x)=\coth(x)-{\frac {1}{x}}\approx {\frac {x}{3}}$ .

Für $x\gg 1$ gilt die Näherung^[1]

$L(x)\approx 1-{\frac {1}{x}}$ .

Umkehrfunktion

Da die Langevin-Funktion keine geschlossen darstellbare Umkehrfunktion hat, gibt es verschiedene Näherungen. Die invertierte Langevin-Funktion wird mit einer Minus-Eins von Spitzklammern umkleidet in Exponentenstellung hinter dem L dargestellt. Diese Umkehrfunktion ist ähnlich wie die Lambertsche W-Funktion nicht elementar darstellbar.

Eine verbreitete Näherung, die im Intervall $(-1,1)$ gilt, wurde von A. Cohen veröffentlicht:^[2]

$L^{\langle -1\rangle }(x)\approx x{\frac {3-x^{2}}{1-x^{2}}}$

Der größte relative Fehler dieser Näherung ist 4,9 % um $|x|=0{,}8$ . Es existieren weitere Näherungen, die weitaus kleinere relative Fehler haben.^[3]^[4]

Die Maclaurinsche Reihe der invertierten Langevin-Funktion lautet wie folgt^[5] und hat den Konvergenzradius 1:

$L^{\langle -1\rangle }(x)\approx 3x+{\frac {9}{5}}x^{3}+{\frac {297}{175}}x^{5}+{\frac {1539}{875}}x^{7}+\dotsb$

Siehe auch

Einzelnachweise

↑ ^{Hochspringen nach: a} ^b ^c Siegmund Brandt: Elektrodynamik. Springer, Berlin 2005, ISBN 3-540-21458-5, S. 293.
↑ A. Cohen: A Padé approximant to the inverse Langevin function. In: Rheologica Acta. 30. Jahrgang, Nr. 3, 1991, S. 270–273, doi: 10.1007/BF00366640.
↑ R. Jedynak: New facts concerning the approximation of the inverse Langevin function. In: Journal of Non-Newtonian Fluid Mechanics. 249. Jahrgang, 2017, S. 8–25, doi: 10.1016/j.jnnfm.2017.09.003.
↑ M. Kröger: Simple, admissible, and accurate approximants of the inverse Langevin and Brillouin functions, relevant for strong polymer deformations and flows. In: Journal of Non-Newtonian Fluid Mechanics. 223. Jahrgang, 2015, S. 77–87, doi: 10.1016/j.jnnfm.2015.05.007.
↑ Laurence A. Belfiore: Physical Properties of Macromolecules. John Wiley & Sons, 2010, ISBN 0-470-55158-5, S. 277 ( eingeschränkte Vorschau in der Google-Buchsuche)

Basierend auf einem Artikel in:

Wikipedia.de