
Magnetisches Dipolmoment
| Physikalische Größe | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | Magnetisches Dipolmoment | ||||||||||||
| Formelzeichen | |||||||||||||
| |||||||||||||
Das magnetische Dipolmoment (oder magnetische Moment)
ist in der Physik ein Maß für die Stärke eines magnetischen Dipols
und analog dem elektrischen
Dipolmoment definiert.
Auf einen magnetischen Dipol wirkt in einem externen Flussdichte
ein Drehmoment
durch das er in die Feldrichtung gedreht wird (:
Kreuzprodukt). Seine potentielle
Energie ist daher abhängig vom Einstellwinkel
zwischen Feldrichtung und magnetischem Moment:
Wichtige Beispiele sind die Kompassnadel und der Elektromotor.
Die Maßeinheit
des magnetischen Moments im Internationalen
Einheitensystem (SI) ist A·m2. Oft
wird das Produkt aus
und der magnetischen
Feldkonstante
verwendet[Anm
1]; dieses hat die SI-Einheit T·m3.
Zustandekommen
- Ein magnetisches Moment kann Folge eines elektrischen Stroms sein:
- Die Stromdichteverteilung
hat ein magnetisches Moment
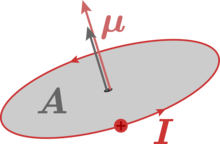
- Für eine ebene Stromschleife ergibt sich daraus
- wobei
die vom Strom
umflossene Fläche ist.
- Dies ist in der Elektrotechnik Grundlage für z.B. Generatoren, Motoren und Elektromagneten.
wird gyromagnetisches Verhältnis genannt. Beispiele sind Elektronen, die durch die Parallelstellung ihrer magnetischen Momente den Ferromagnetismus der Elemente der Eisengruppe und der Seltenen Erden hervorrufen. Ferromagnetische Materialien werden als Dauermagneten oder als Eisenkerne in Elektromagneten und Transformatoren verwendet.
Beispiele
Ebene Leiterschleife
Für eine geschlossene Leiterschleife gilt
Dabei bezeichnet
die Stromdichte am Ort
ein Volumenintegral
die Stromstärke durch die Leiterschleife
ein Wegintegral entlang der Leiterschleife.
Damit folgt für das magnetische Dipolmoment:
mit dem Normalenvektor
auf der ebenen Fläche
.
Der Vektor
ist dabei so orientiert, dass er bei gegen
dem Uhrzeigersinn fließendem Strom nach oben zeigt.
Stromdurchflossene lange Spule
Das magnetische Moment einer stromdurchflossenen Spule ist das
Produkt aus Windungszahl ,
Stromstärke
und Fläche
:
Darin ist
der zur Fläche
gehörende Vektor.
Geladenes Teilchen auf einer Kreisbahn
Klassisch
Ist der Kreisstrom dadurch verursacht, dass ein Teilchen mit der Masse
und der Ladung
auf einer Kreisbahn (Radius
,
Umlaufperiode
)
kreist, ergibt diese Formel
Das magnetische Moment ist also fest mit dem Drehimpuls
verknüpft. Der konstante Faktor
ist das gyromagnetische
Verhältnis für bewegte Ladung auf der Kreisbahn. (Bei der Umrechnung wird
die Winkelgeschwindigkeit
benutzt.)
Quantenmechanisch
Die klassische Formel spielt in der Atom- und Kernphysik eine große Rolle,
denn sie gilt auch in der Quantenmechanik, und ein wohlbestimmter Drehimpuls
gehört zu jedem Energieniveau eines einzelnen Atoms oder Kerns. Da der
Drehimpuls der räumlichen Bewegung (Bahndrehimpuls, im
Unterschied zum Spin) nur ganzzahlige Vielfache
der Konstanten
(Plancksches
Wirkungsquantum) betragen kann[Anm
2], hat auch das magnetische Bahnmoment eine als Magneton
bezeichnete kleinste „Einheit“:
Wird für
die Elementarladung
eingesetzt, ergibt sich für das Elektron das Bohr’sche
Magneton
,
für das Proton das Kernmagneton
.
Da die Protonenmasse
knapp 2000-mal größer ist als die Elektronenmasse
,
ist das Kernmagneton um denselben Faktor kleiner als das Bohr’sche Magneton.
Das magnetische Moment von Teilchen und Kernen
Teilchen
und Atomkerne mit einem Spin
besitzen ein magnetisches Spinmoment
,
das zu ihrem Spin parallel (oder antiparallel) ist, aber im Verhältnis zum Spin
eine andere Größe hat, als wenn es von einem gleich großen Bahndrehimpuls
herrührte. Dies wird durch den anomalen Landé-Faktor
des Spins
ausgedrückt. Man schreibt für Elektron (
)
und Positron (
)
mit dem Bohr’schen Magneton
,
für Proton (p) und Neutron (n)
mit dem Kernmagneton
,
und entsprechend für andere Teilchen. Die Dipolmomente der Atomkerne und ihre Auswirkungen wie die Hyperfeinstruktur sind im Vergleich zur auf Elektron-Dipolmomenten beruhenden Feinstrukturaufspaltung sehr schwach und schwer zu beobachten.
Für das Myon wird im Magneton statt der Masse des Elektrons die des Myons eingesetzt, für die Quarks ihre jeweilige Konstituentenmasse und drittelzahlige elektrische Ladung.
Liegt das magnetische Moment antiparallel zum Spin, ist der g-Faktor negativ. Allerdings wird diese Vorzeichenkonvention nicht durchgängig angewendet, so dass häufig der g-Faktor z.B. des Elektrons als positiv angegeben ist.[Anm 3]
| Teilchen | Spin-g-Faktor |
|---|---|
| Elektron |
|
| Myon |
|
| Proton |
|
| Neutron |
Die eingeklammerten Ziffern geben die geschätzte Standardabweichung an.
Nach der Dirac-Theorie
ist der Landé-Faktor der fundamentalen Fermionen
exakt ,
quantenelektrodynamisch
wird ein Wert von etwa
vorhergesagt. Präzise Messungen an Elektron
bzw. Positron sowie am Myon stimmen damit hervorragend
überein, einschließlich der vorhergesagten kleinen Differenz zwischen Elektron
und Myon, und bestätigen so die Dirac-Theorie und die Quantenelektrodynamik. Die
stark abweichenden g-Faktoren für die Nukleonen sind, allerdings mit
Abweichungen im Prozentbereich, durch ihren Aufbau aus jeweils drei Konstituentenquarks
zu erklären.
Weisen die Teilchen (z.B. Elektronen, die an einen Atomkern gebunden
sind) zusätzlich einen Bahndrehimpuls auf, so ist das magnetische Moment die
Summe aus ,
dem oben betrachteten magnetischen Moment des Spins, und
,
demjenigen des Bahndrehimpulses:
.
Magnetisches Feld eines magnetischen Dipols
Ein magnetischer Dipol
am Koordinatenursprung
führt am Ort
zu einer magnetischen Flussdichte
.
Darin ist
die magnetische
Feldkonstante. Außer am Ursprung, wo das Feld divergiert, verschwindet
überall sowohl die Rotation
als auch die Divergenz
dieses Feldes. Das zugehörige Vektorpotential
ergibt sich zu
,
wobei
ist. Mit der magnetischen
Feldstärke
beträgt das magnetische Skalarpotential
.
Kraft- und Momentwirkung zwischen magnetischen Dipolen
Kraftwirkung zwischen zwei Dipolen
Die Kraft, die von Dipol 1 auf Dipol 2 ausgeübt wird, ist
Es ergibt sich
worin
der Einheitsvektor
ist, der von Dipol 1 zu Dipol 2 zeigt und
der Abstand zwischen den beiden Magneten ist. Die Kraft auf Dipol 1 ist
reziprok.
Drehmomentwirkung zwischen zwei Dipolen
Das Drehmoment, das von Dipol 1 auf Dipol 2 ausgeübt wird, ist
worin
das von Dipol 1 erzeugte Feld am Ort von Dipol 2 ist (s.o.). Das
Drehmoment auf Dipol 1 ist reziprok.
In Anwesenheit mehrerer Dipole können die Kräfte oder Momente überlagert werden. Da weichmagnetische Werkstoffe einen feldabhängigen Dipol ausbilden, sind diese Gleichungen nicht anwendbar.
Literatur
- John David Jackson: Klassische Elektrodynamik. Anhang über Einheiten und Dimensionen. 4. Auflage. De Gruyter, Berlin 2006, ISBN 3-11-018970-4.
Anmerkungen
- ↑ a
b
In älteren Büchern, z.B. W. Döring,
Einführung in die Theoretische Physik, Sammlung Göschen, Band II
(Elektrodynamik), wird als magnetisches Moment das
-fache des hier angegebenen Wertes definiert. Dann heißt es z.B.
und
ist definiert nicht als Magnetisierung durch Volumen, sondern als magnetische Polarisation
durch Volumen. In Materie ist ja allgemein
und
(wegen
) Alte und neue Definition sind daher voll äquivalent. Die offizielle Einigung auf die neue CODATA-Definition geschah 2010.
- ↑ Genauer: das gilt für die Komponente des Drehimpulsvektors längs einer Achse.
- ↑ Praktisch wichtig ist das Vorzeichen nur dann, wenn es um den Drehsinn der Larmorpräzession oder das Vorzeichen der paramagnetischen Spinpolarisation geht. Dementsprechend werden die Vorzeichen in der Literatur nicht ganz einheitlich gehandhabt.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 05.01. 2022